高维混沌系统的多元函数投影同步及其保密通信方案

doi:10.19596/j.cnki.1001-246x.8550

摘要/Abstract

摘要：

提出一种改进的函数投影同步方案——多元函数投影同步。与现有的比例因子为一元函数的函数投影同步方案不同，本文讨论的比例因子为多元函数。在该方案下，系统间的同步行为更复杂、更难以预测，驱动与响应系统将在更高的维度中展现出相关性。基于改进的主动控制方法，研究四维能源系统和超混沌蔡氏系统的多元函数投影同步问题，并设计同步控制器。在数值模拟中，分别针对比例因子为多元线性函数和多元非线性函数情况进行同步仿真，实现了系统之间的多元函数投影同步。利用上述同步，设计相应的保密通信方案，以正弦信号和灰度图像信号作为信息信号进行保密通信仿真，并通过引入小波阈值去噪算法进行抗噪声模拟。结果表明: 提出的同步方案可行，所设计的保密通信方法有效，具备较好的保密性和稳健性。

关键词: 多元函数投影同步, 改进的主动控制, 保密通信, 小波阈值去噪

Abstract:

A modified function projective synchronization scheme, multivariable function projective synchronization, is proposed. Different from existing function projective synchronization schemes whose scaling factor is unary function, the scaling factor discussed in this scheme is multivariable function. It implies that synchronization behavior of the proposed scheme is more complicated and more unpredictable. The driver and responding system show correlation in a higher dimension. With modified active control method, controller of the synchronization is designed. In numerical simulations, four-dimensional energy resources system and a new hyperchaotic Chua system are investigated. Multivariable function projective synchronization with two types of scaling factor between two systems are achieved. Based on the synchronization, a secure communication scheme is designed. A secure communication simulation is carried out with sinusoidal signal and gray image signal as information signals. Meanwhile, anti-noise simulation is performed with a wavelet threshold denoising algorithm. It shows that the synchronization method is feasible, and the secure communication scheme is effective.

Key words: multivariable function projective synchronization, modified active control, secure communication, wavelet threshold denoising

李震波, 唐叶芝. 高维混沌系统的多元函数投影同步及其保密通信方案[J]. 计算物理, 2023, 40(1): 91-105.

Zhenbo LI, Yezhi TANG. Multivariable Function Projective Synchronization of High Dimensional Chaotic Systems and Its Secure Communication Scheme[J]. Chinese Journal of Computational Physics, 2023, 40(1): 91-105.

图/表 16

表1 各类常见的投影同步

Table 1 Different kinds of projective synchronization

同步误差向量	同步类型	比例因子Γ
e_i=x_i-Γy_i 其中x_i为驱动向量，y_i为响应向量，Γ为比例因子	完全同步	Γ=1
	投影同步	Γ为常数，大小由驱动系统初值决定
	广义投影同步	Γ为常数，大小可任意指定
	一元函数投影同步	Γ为时间t的一元函数
	二元函数投影同步	Γ为二元函数
	多元函数投影同步	Γ为多元函数

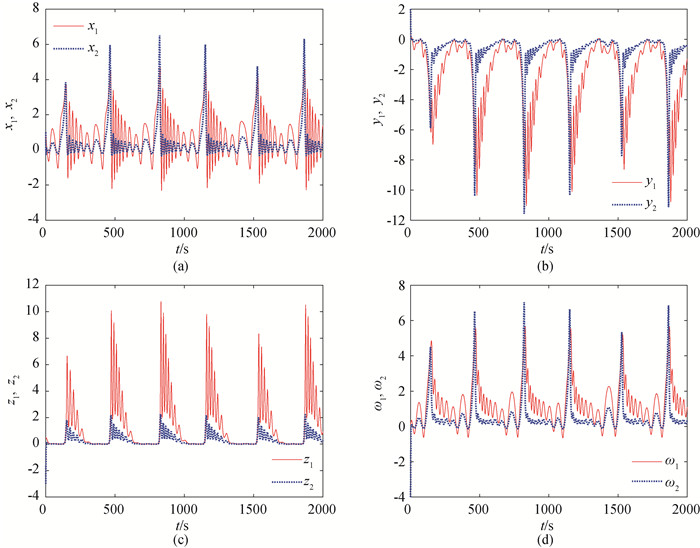
图1 系统(8)和系统(9)在比例因子Γ1下同步的时间历程(a) x1与x2的时间历程；(b) y1与y2的时间历程；(c) z1与z2的时间历程；(d) ω1与ω2的时间历程

Fig.1 Time response of System (8) and (9) with scaling function Γ1 (a) time response of x1 and x2; (b) time response of y1 and y2; (c) time response of z1 and z2; (d) time response of ω1 and ω2

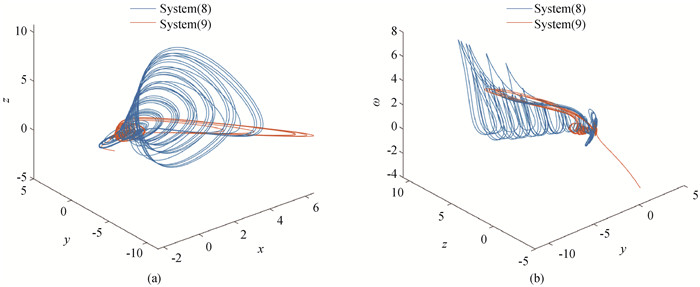
图2 系统(8)和系统(9)在比例因子Γ1下同步的相图(a) x-y-z空间的相图；(b) y-z-ω空间的相图

Fig.2 Phase portraits of System (8) and (9) with scaling function Γ1 (a) phase portraits in x-y-z space; (b) phase portraits in y-z-ω space

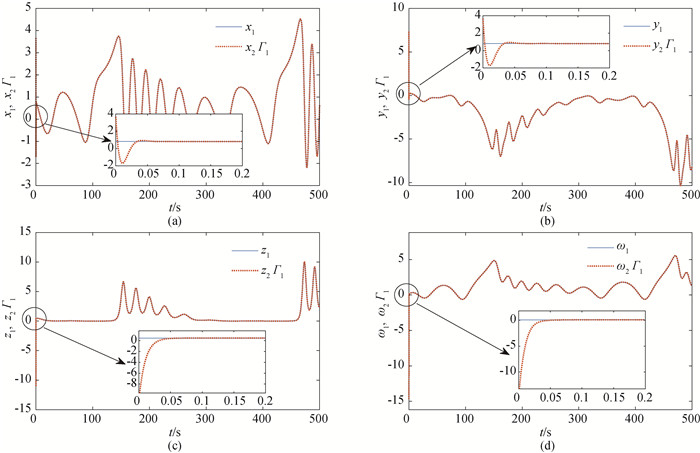
图3 系统(8)和系统(9)关于比例因子Γ1下的同步结果(a) x1与x2的同步结果; (b) y1与y2的同步结果；(c) z1与z2的同步结果；(d) ω1与ω2的同步结果

Fig.3 Synchronization results of System (8) and (9) with scaling function Γ1 (a) synchronization results of x1 and x2; (b) synchronization results of y1 and y2; (c) synchronization results of z1 and z2; (d) synchronization results of ω1 and ω2

图4 系统(8)和系统(9)在比例因子Γ1下的同步误差曲线

Fig.4 Synchronization errors of System (8) and (9) with scaling function Γ1

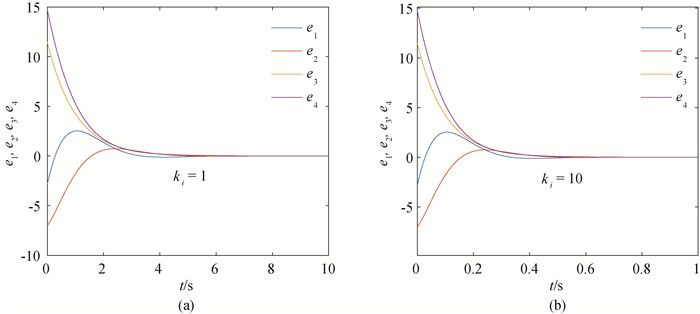
图5 系统(8)和系统(9)在比例因子Γ1下的同步误差曲线(a) ki=1；(b) ki=10

Fig.5 Synchronization errors of System (8) and (9) with scaling function Γ1 at different ki (a) ki=1; (b) ki=10

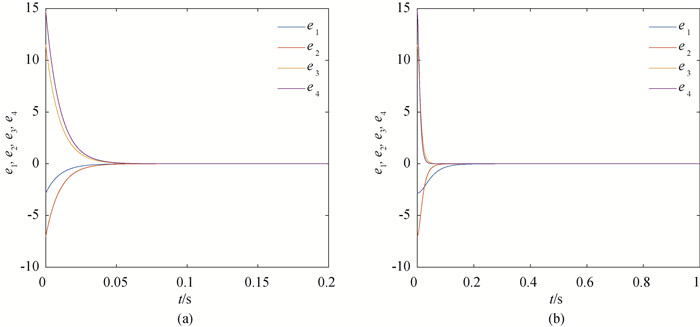
图6 系统(8)和系统(9)的同步误差曲线(a) 非线性反馈控制法；(b) 自适应反馈控制法

Fig.6 Synchronization errors of System (8) and (9) (a) nonlinear feedback method, (b) adaptive feedback method

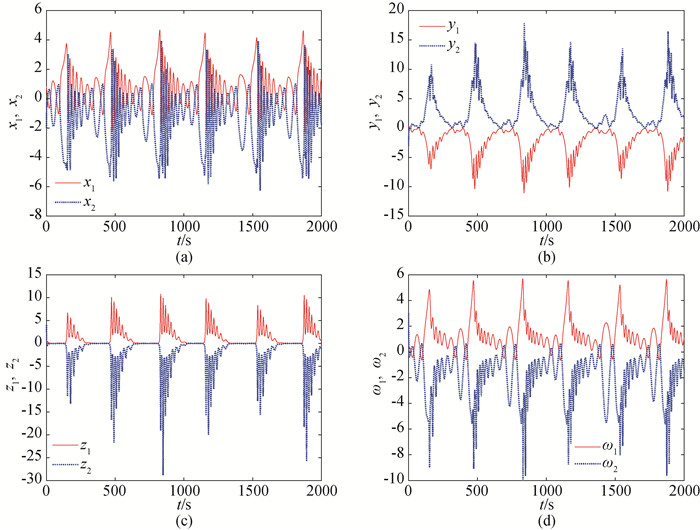
图7 系统(8)和系统(9)在比例因子Γ2下同步的时间历程(a) x1与x2的时间历程；(b) y1与y2的时间历程；(c) z1与z2的时间历程；(d) ω1与ω2的时间历程

Fig.7 Time response of System (8) and (9) with scaling function Γ2 (a) time response of x1 and x2; (b) time response of y1 and y2; (c) time response of z1 and z2; (d) time response of ω1 and ω2

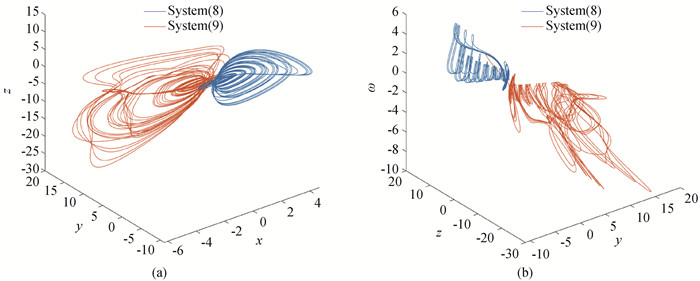
图8 系统(8)和系统(9)在比例因子Γ2下同步的相图(a) x-y-z空间的相图；(b) y-z-ω空间的相图

Fig.8 Phase portraits of System (8) and (9) with scaling function Γ2 (a) phase portrait in x-y-z space; (b) phase portrait in y-z-ω space

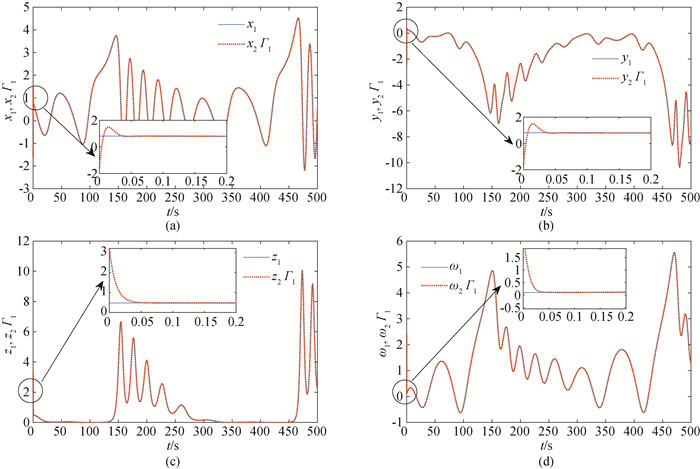
图9 系统(8)和系统(9)在比例因子Γ2下的同步结果(a) x1与x2的同步结果；(b) y1与y2的同步结果；(c) z1与z2的同步结果; (d) ω1与ω2的同步结果

Fig.9 Synchronization results of System (8) and (9) with scaling function Γ2 (a) synchronization results of and x2; (b) synchronization results of y1 and y2; (c) synchronization results of z1 and z2; (d) synchronization results of ω1 and ω2

图10 系统(8)和系统(9)在比例因子Γ2下的同步误差曲线

Fig.10 Synchronization errors of System (8) and (9) with scaling function Γ2

图11 小波阈值去噪原理

Fig.11 A flow chart of wavelet threshold denoising

图12 保密通信原理图

Fig.12 A flow chart of secure communication scheme

图13 通信信号θ(t)在不同信噪比下的图像

Fig.13 Pictures of communication signal θ(t) at different SNR

图14 不同信噪比下正弦信号的恢复信号

Fig.14 Recovered signal of sinusoidal signal at different SNR

图15 不同信噪比下灰度图像的恢复信号

Fig.15 Recovered image of grayscale image at different SNR

参考文献 33

1	PECORA L M , CARROLL T L . Synchronization in chaotic systems[J]. Physical Review Letters, 1990, 64 (8): 821- 824. DOI
2	SHI J P , LI P S , LIU G P . Synchronization control and parameter identification for unified chaotic system based on improved clonal selection algorithm[J]. Chinese Journal of Computational Physics, 2020, 37 (2): 240- 252.
3	YU H T , WANG J , LIU Q X , et al. Chaotic phase synchronization in a modular neuronal network of small-world subnetworks[J]. Chaos, 2011, 21 (4): 043125. DOI
4	FENG C F , YANG H J . Projective-lag synchronization scheme between two different discrete-time chaotic systems[J]. International Journal of Non-linear Mechanics, 2020, 121, 103451. DOI
5	MOSKALENKO O I , KORONOVSKII A A , SELSKII A O , et al. On multistability near the boundary of generalized synchronization in unidirectionally coupled chaotic systems[J]. Chaos, 2021, 31 (8): 083106. DOI
6	QIAN H , YU H J . Application of SC projective synchronization method in secure communication[J]. Chinese Journal of Computational Physics, 2016, 33 (1): 118- 126.
7	XUE W , ZHANG Y C . Application of conservative hyperchaos in digital image encryption[J]. Chinese Journal of Computational Physics, 2020, 37 (4): 498- 504.
8	KANG Z J , CANG S J , LI Y . A conservative-chaos-based key distribution protocol and image encryption algorithm[J]. Chinese Journal of Computational Physics, 2021, 38 (2): 232- 243.
9	MAINIERI R , REHACEK J . Projective synchronization in three-dimensional chaotic systems[J]. Physical Review Letters, 1999, 82 (15): 3042- 3045. DOI
10	CHEN Y , LI X . Function projective synchronization between two identical chaotic systems[J]. International Journal of Modern Physics C, 2007, 18 (5): 883- 888. DOI
11	DU H Y , ZENG Q S , WANG C H . Function projective synchronization of different chaotic systems with uncertain parameters[J]. Physics Letters A, 2008, 372 (33): 5402- 5410. DOI
12	SUDHEER K S , SABIR M . Adaptive modified function projective synchronization between hyperchaotic Lorenz system and hyperchaotic Lu system with uncertain parameters[J]. Physics Letters A, 2009, 373 (41): 3743- 3748. DOI
13	DU H Y , ZENG Q S , WANG C H . Modified function projective synchronization of chaotic system[J]. Chaos Solitons & Fractals, 2009, 42 (4): 2399- 2404.
14	YU Y G , LI H X . Adaptive generalized function projective synchronization of uncertain chaotic systems[J]. Nonlinear Analysis-Real World Applications, 2010, 11 (4): 2456- 2464. DOI
15	YUAN M M , WANG W P , LUO X , et al. Exponential lag function projective synchronization of memristor-based multidirectional associative memory neural networks via hybrid control[J]. Modern Physics Letters B, 2018, 32 (9): 1850116. DOI
16	CHAI X L , GAN Z H . Function Projective lag synchronization of chaotic systems with certain parameters via adaptive-impulsive control[J]. International Journal of Automation and Computing, 2019, 16 (2): 238- 247. DOI
17	WANG C , ZHANG H L , FAN W H , et al. Finite-time function projective synchronization control method for chaotic wind power systems[J]. Chaos Solitons & Fractals, 2020, 135, 109756.
18	EL-DESSOKY M M , ALZAHRANI E , AL-REHILY N . Control and adaptive modified function projective synchronization of a new hyperchaotic system[J]. Alexandria Engineering Journal, 2021, 60 (4): 3985- 3990. DOI
19	LI Z B , TANG J S . Generalized binary function projective synchronization of chaotic systems with unknown parameters[J]. Optik, 2017, 137, 101- 107. DOI
20	李震波, 赵小山, 王靖. 基于改进的主动控制法实现混沌系统广义投影同步[J]. 物理学报, 2011, 60 (5): 113- 120.
21	SUN M , JIA Q , TIAN L X . A new four-dimensional energy resources system and its linear feedback control[J]. Chaos Solitons & Fractals, 2009, 39 (1): 101- 108.
22	RECH P C , ALBUQUERQUE H A . A hyperchaotic Chua system[J]. International Journal of Bifurcation and Chaos, 2009, 19 (11): 3823- 3828. DOI
23	ROBINSON R C . An introduction to dynamical systems: Continuous and discrete[M]. New Jersey: Prentice Hall, 2004.
24	HU J B , HAN Y , ZHAO L D . Synchronizing chaotic systems using control based on a special matrix structure and extending to fractional chaotic systems[J]. Communications in Nonlinear Science and Numerical Simulation, 2010, 15 (1): 115- 123. DOI
25	LI W J , LI P , JIA M M . Chaos control and chaos synchronization of a multi-wing chaotic system and its application in multi-frequency weak signal detection[J]. Aip Advances, 2021, 11 (9): 095003. DOI
26	方洁, 娄新杰, 方娜, 等. 多混沌系统自适应组合函数投影同步[J]. 东北师大学报(自然科学版), 2020, 52 (1): 98- 103.
27	李爽, 徐伟, 李瑞红, 等. 异结构系统混沌同步的新方法[J]. 物理学报, 2006, (11): 5681- 5687.
28	REN L , ZHANG G S . Adaptive projective synchronization for a class of switched chaotic systems[J]. Mathematical Methods in The Applied Sciences, 2019, 42 (18): 6192- 6204. DOI
29	段青, 李凤祥, 田兆垒. 一种改进的小波阈值信号去噪方法[J]. 计算机仿真, 2009, 26 (4): 348- 351.
30	吴叶丽, 行鸿彦, 李瑾, 等. 改进阈值函数的小波去噪算法[J]. 电子测量与仪器学报, 2022, 36 (4): 9- 16.
31	付宏睿, 董永刚, 张建刚. 基于新四维混沌系统的复杂网络的混沌保密通信及噪声研究[J]. 东北师大学报(自然科学版), 2018, 50 (4): 73- 77.
32	王晓燕, 瞿少成, 田文汇, 等. 异结构混沌系统同步及其在保密通信中的应用[J]. 计算机应用研究, 2009, 26 (5): 1874- 1876.
33	于娜, 丁群, 陈红. 异结构系统混沌同步及其在保密通信中的应用[J]. 通信学报, 2007, (10): 73- 78.

[1]	贾雅琼, 俞斌. 基于重复混沌扩频序列的差分混沌键控系统[J]. 计算物理, 2022, 39(4): 491-497.
[2]	钱慧, 于洪洁. SC混沌比例投影同步方法在保密通信中的应用[J]. 计算物理, 2016, 33(1): 117-126.