计算物理 ›› 2023, Vol. 40 ›› Issue (3): 343-352.DOI: 10.19596/j.cnki.1001-246x.8559
收稿日期:2022-05-11
出版日期:2023-05-25
发布日期:2023-07-22
通讯作者:
热合买提江·依明
作者简介:裴静娴(1995—),女,硕士研究生,研究方向为数值计算及其模拟, E-mail: 978100780@qq.com
基金资助:
Jingxian PEI( ), Imin RAHMATJAN*(
), Imin RAHMATJAN*( )
)
Received:2022-05-11
Online:2023-05-25
Published:2023-07-22
Contact:
Imin RAHMATJAN
摘要:
考虑虚拟粒子法在解决边界问题时因粒子搜索量大而增加冗余计算等因素,转而只在计算域内部采用SPH修正方法,边界处使用有限差分方法,从而实现一种基于有限差分法的SPH边界处理算法。以热传导问题为例,对数值模拟结果进行验证。结果表明:采用提出的边界处理方法对固定和对流边界热传导问题进行求解,解析解与数值解吻合程度较高,数值模拟可靠有效。两种算法优势互补,为相关边值问题的处理提供了思路。
裴静娴, 热合买提江·依明. 基于有限差分法的SPH边界处理算法及其应用[J]. 计算物理, 2023, 40(3): 343-352.
Jingxian PEI, Imin RAHMATJAN. SPH Boundary Algorithm Based on Finite Difference Method and Its Application[J]. Chinese Journal of Computational Physics, 2023, 40(3): 343-352.
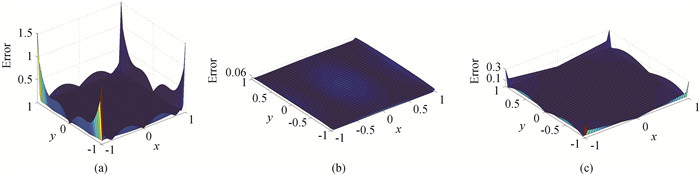
图2 二元函数二阶导数计算绝对误差(a) f1(x) = sin(πxy),(b) f2(x) =exp(-x2-y2),(c) f3(x) =(xy)3
Fig.2 Absolute errors of second derivative calculation of binary functions (a) f1(x) = sin(πxy), (b) f2(x) =exp(-x2-y2), (c) f3(x) =(xy)3
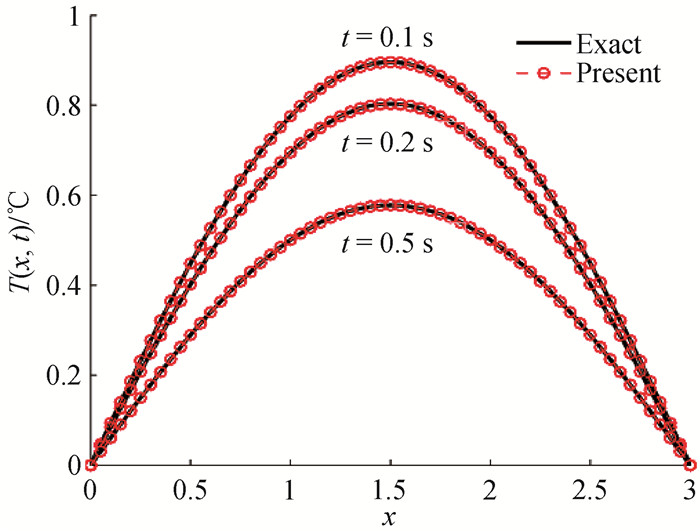
图3 一维固定边界条件在0.1 s,0.2 s和0.5 s时刻解析解与数值解温度曲线
Fig.3 Temperature curves of analytical and numerical solutions at 0.1 s, 0.2 s and 0.5 s for one-dimensional fixed boundary conditions
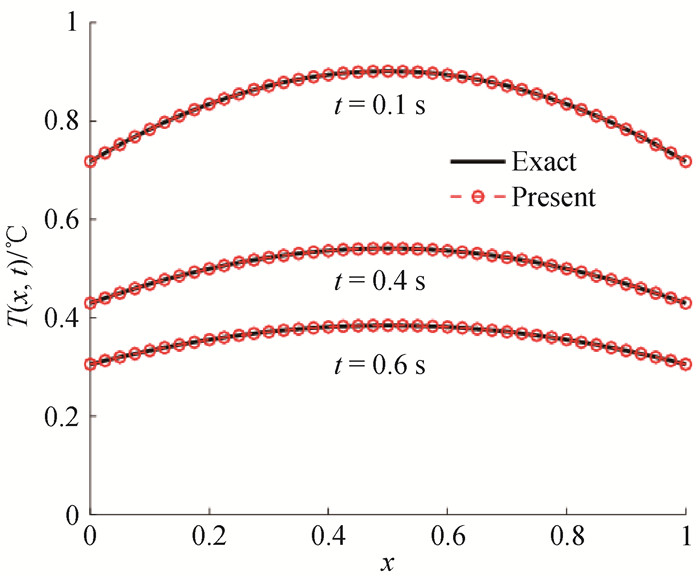
图4 一维对流边界条件在0.1 s,0.4 s和0.6 s时刻解析解与数值解温度曲线
Fig.4 Temperature curves of analytical and numerical solutions for one-dimensional convectionboundary conditions at 0.1 s, 0.4 s and 0.6 s
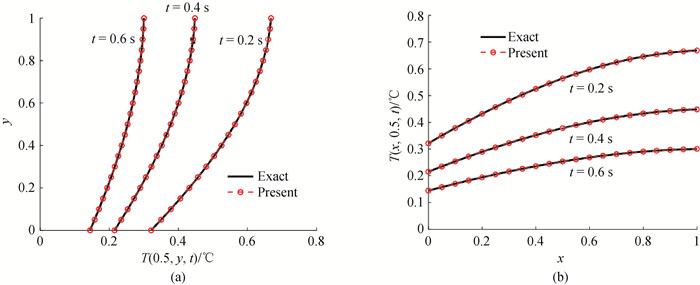
图5 二维固定边界条件在0.2 s,0.4 s和0.6 s时刻数值解与解析解温度曲线(a) x = 0.5, (b) y = 0.5
Fig.5 Temperature curves of numerical solutions and analytical solutions for two-dimensional fixed boundary conditions at 0.2 s, 0.4 s and 0.6 s (a)x = 0.5, (b) y = 0.5
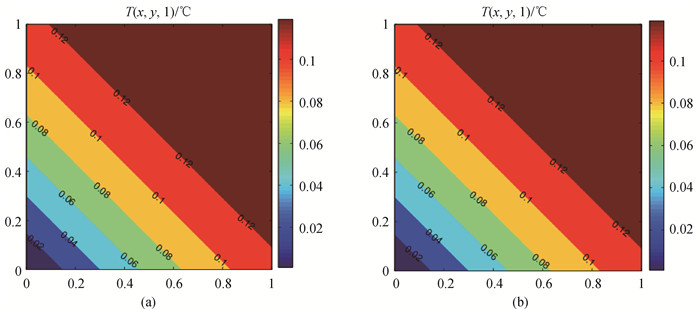
图6 二维固定边界条件问题t=1 s时的温度分布(a)解析解,(b)数值解
Fig.6 Temperature distributions of two-dimensional fixed boundary condition problem at t=1 s (a) analytical solution, (b) numerical solution
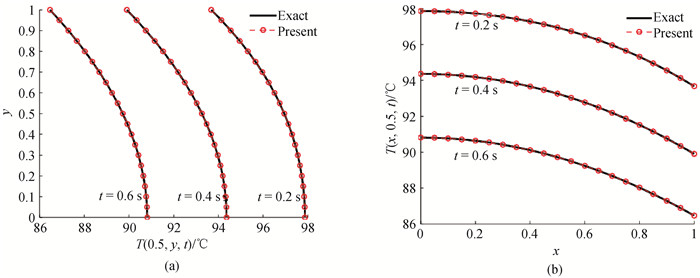
图7 二维对流边界条件在0.2 s,0.4 s和0.6 s时刻数值解与解析解温度曲线(a)x=0.5,(b)y=0.5
Fig.7 Temperature curves of numerical solutions and analytical solutions for two-dimensional convective boundary conditions at 0.2 s, 0.4 s and 0.6 s (a)x=0.5, (b)y=0.5
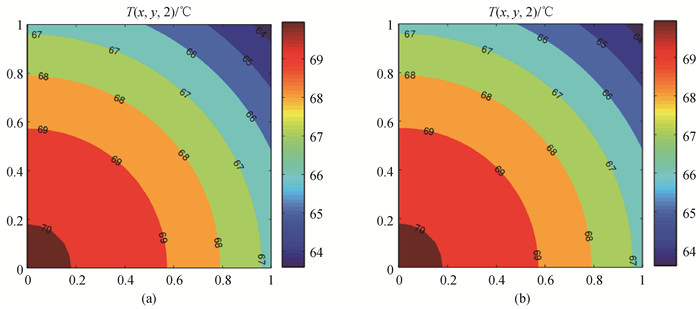
图8 二维对流边界问题t = 2 s时温度分布(a)解析解,(b)数值解
Fig.8 Temperature distributions of two-dimensional convective boundary problem at t=2s (a) analytical solution, (b) numerical solution
| 1 |
|
| 2 |
DOI |
| 3 |
DOI |
| 4 |
|
| 5 |
|
| 6 |
DOI |
| 7 |
DOI |
| 8 |
DOI |
| 9 |
|
| 10 |
DOI |
| 11 |
DOI |
| 12 |
|
| 13 |
李建成, 袁德奎, 陶建华. 二阶核近似有限粒子方法的改进[J]. 水动力学研究与进展, 2013, 28(3): 260- 273.
|
| 14 |
郑兴, 段文洋. 光滑粒子流体动力学二阶算法精度研究[J]. 水科学进展, 2008, 19(6): 821- 827.
DOI |
| 15 |
DOI |
| 16 |
DOI |
| 17 |
BELYTSCHKO T, KRONGAUZ Y, et al. On the completness of meshfree particle methods[C]. Int J Numer Methods Engrg, 1998, 43(5): 785-819.
|
| 18 |
|
| 19 |
DOI |
| 20 |
DOI |
| 21 |
DOI |
| 22 |
DOI |
| 23 |
DOI |
| 24 |
DOI |
| 25 |
|
| 26 |
热合买提江·依明, 阿合买提江·依明江. 避免核函数导数的二阶导数核近似方法的修正[J]. 计算力学学报, 2018, 35(4): 494- 499.
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
程玉民. 无网格方法[M]. 北京: 科学出版社, 2015.
|
| 31 |
|
| [1] | 袁文强, 赵忠海, 乔宾. 辐射流体程序中的非局域电子热传导[J]. 计算物理, 2023, 40(2): 232-240. |
| [2] | 孙杰, 程仁寨, 李云, 房洪杰, 汪洪波, 陈小龙. Au@碳球复合结构中Au颗粒位置调控光吸收[J]. 计算物理, 2021, 38(6): 735-741. |
| [3] | 李康, 李守先, 刘娜. 强爆炸火球辐射流体自适应网格高精度数值模拟[J]. 计算物理, 2021, 38(2): 146-152. |
| [4] | 王兆清, 钱航, 李金. 移动边界问题的时空域正则区域迭代配点法[J]. 计算物理, 2021, 38(1): 16-24. |
| [5] | 柴国亮, 苏军伟, 王乐. 一种保持二阶精度的反距离加权空间插值算法[J]. 计算物理, 2020, 37(4): 393-402. |
| [6] | 张林, 葛永斌. 二维半线性扩散反应方程的高精度全隐格式及其多重网格方法[J]. 计算物理, 2020, 37(3): 307-319. |
| [7] | 王磊磊, 纪乐, 马文涛. FGMs稳态热传导分析的重心Lagrange插值配点法[J]. 计算物理, 2020, 37(2): 173-181. |
| [8] | 郑洲顺, 刘振, 耿婷婷, 吴晓新, 汤慧萍, 王建忠. 金属纤维烧结过程的分数阶模型[J]. 计算物理, 2019, 36(5): 595-602. |
| [9] | 高云, 邹丽, 宗智. 基于有限差分法刚性圆柱体涡激振动响应特性数值研究[J]. 计算物理, 2019, 36(1): 53-59. |
| [10] | 陈恭, 王一正, 王烨, 张纯禹. 缩减基有限元方法快速求解参数化偏微分方程[J]. 计算物理, 2018, 35(5): 515-524. |
| [11] | 周焕林, 严俊, 余波, 陈豪龙. 基于改进布谷鸟算法识别瞬态热传导问题的导热系数[J]. 计算物理, 2018, 35(2): 212-220. |
| [12] | 祁鹏, 刘慧卿, 庞占喜, 刘化普, 陈宇. SAGD循环预热储层温度分析模型[J]. 计算物理, 2018, 35(1): 64-70. |
| [13] | 葛永斌, 蔡志权. 奇异退化扩散反应方程的高阶紧致差分及网格自适应方法[J]. 计算物理, 2017, 34(3): 309-319. |
| [14] | 刘广东. 一种乳腺癌检测的改进微波共焦成像方法[J]. 计算物理, 2017, 34(1): 82-88. |
| [15] | 吴自库, 李福乐, DO Young Kwak. 一维热传导方程热源反问题基于最小二乘法的正则化方法[J]. 计算物理, 2016, 33(1): 49-56. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||
版权所有 © 《计算物理》编辑部
地址:北京市海淀区丰豪东路2号 邮编:100094 E-mail:jswl@iapcm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发
