Chinese Journal of Computational Physics ›› 2022, Vol. 39 ›› Issue (6): 666-676.DOI: 10.19596/j.cnki.1001-246x.8495
• Research Reports • Previous Articles Next Articles
Shuting FENG( ), Houping DAI*(
), Houping DAI*( ), Tongzheng SONG
), Tongzheng SONG
Received:2021-12-21
Online:2022-11-25
Published:2023-04-01
Contact:
Houping DAI
Shuting FENG, Houping DAI, Tongzheng SONG. Lattice Boltzmann Method for Two-dimensional Fractional Reaction-Diffusion Equations[J]. Chinese Journal of Computational Physics, 2022, 39(6): 666-676.
Add to citation manager EndNote|Ris|BibTeX
URL: http://www.cjcp.org.cn/EN/10.19596/j.cnki.1001-246x.8495
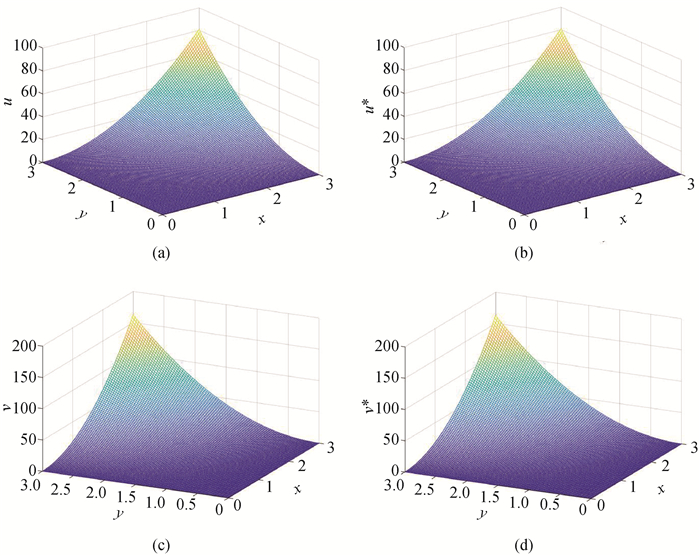
Fig.1 Evolution of exact solutions and LBM numerical solutions (a) exact solution of u; (b) numerical solution of u; (c) exact solution of v; (d) numerical solution of v
| T | GRE(N, M, Δt, u) | GRE(N, M, Δt, v) | CPU/s |
| 0.2 | 2.052 3 × 10-4 | 2.960 8 × 10-4 | 14.1 |
| 0.4 | 5.730 8 × 10-5 | 2.115 2 × 10-4 | 25.5 |
| 0.6 | 1.686 1 × 10-4 | 1.265 0 × 10-4 | 35.8 |
| 0.8 | 3.499 2 × 10-4 | 6.430 0 × 10-5 | 47.1 |
| 1 | 5.496 1 × 10-4 | 7.912 7 × 10-5 | 58.9 |
Table 1 The global relative error and CPU at different moments
| T | GRE(N, M, Δt, u) | GRE(N, M, Δt, v) | CPU/s |
| 0.2 | 2.052 3 × 10-4 | 2.960 8 × 10-4 | 14.1 |
| 0.4 | 5.730 8 × 10-5 | 2.115 2 × 10-4 | 25.5 |
| 0.6 | 1.686 1 × 10-4 | 1.265 0 × 10-4 | 35.8 |
| 0.8 | 3.499 2 × 10-4 | 6.430 0 × 10-5 | 47.1 |
| 1 | 5.496 1 × 10-4 | 7.912 7 × 10-5 | 58.9 |
| α | N | GRE(N, M, Δt, u) | Order1(u) | GRE(N, M, Δt, v) | Order1(v) |
| 1.1 | 4 | 6.183 8 × 10-2 | 6.434 2 × 10-2 | ||
| 8 | 1.970 4 × 10-2 | 1.650 0 | 2.175 6 × 10-2 | 1.564 3 | |
| 16 | 4.885 2 × 10-3 | 2.012 0 | 6.162 1 × 10-3 | 1.819 9 | |
| 32 | 8.444 8 × 10-4 | 2.532 3 | 1.560 9 × 10-3 | 1.981 0 | |
| 64 | 2.409 2 × 10-4 | 1.809 5 | 3.051 2 × 10-4 | 2.354 9 | |
| 1.3 | 4 | 6.353 8 × 10-2 | 6.438 9 × 10-2 | ||
| 8 | 2.097 4 × 10-2 | 1.599 0 | 2.183 6 × 10-2 | 1.560 1 | |
| 16 | 5.581 2 × 10-3 | 1.910 0 | 6.246 6 × 10-3 | 1.805 6 | |
| 32 | 1.157 5 × 10-3 | 2.269 6 | 1.633 2 × 10-3 | 1.935 4 | |
| 64 | 1.994 9 × 10-4 | 2.536 6 | 3.606 0 × 10-4 | 2.179 2 | |
| 1.5 | 4 | 6.448 4 × 10-2 | 6.442 7 × 10-2 | ||
| 8 | 2.184 1 × 10-2 | 1.561 9 | 2.192 5 × 10-2 | 1.555 1 | |
| 16 | 6.174 5 × 10-3 | 1.822 6 | 6.359 5 × 10-3 | 1.785 6 | |
| 32 | 1.508 5 × 10-3 | 2.033 2 | 1.746 7 × 10-3 | 1.864 3 | |
| 64 | 2.393 2 × 10-4 | 2.656 1 | 4.619 3 × 10-4 | 1.918 9 |
Table 2 Error analysis and convergence rate under different α
| α | N | GRE(N, M, Δt, u) | Order1(u) | GRE(N, M, Δt, v) | Order1(v) |
| 1.1 | 4 | 6.183 8 × 10-2 | 6.434 2 × 10-2 | ||
| 8 | 1.970 4 × 10-2 | 1.650 0 | 2.175 6 × 10-2 | 1.564 3 | |
| 16 | 4.885 2 × 10-3 | 2.012 0 | 6.162 1 × 10-3 | 1.819 9 | |
| 32 | 8.444 8 × 10-4 | 2.532 3 | 1.560 9 × 10-3 | 1.981 0 | |
| 64 | 2.409 2 × 10-4 | 1.809 5 | 3.051 2 × 10-4 | 2.354 9 | |
| 1.3 | 4 | 6.353 8 × 10-2 | 6.438 9 × 10-2 | ||
| 8 | 2.097 4 × 10-2 | 1.599 0 | 2.183 6 × 10-2 | 1.560 1 | |
| 16 | 5.581 2 × 10-3 | 1.910 0 | 6.246 6 × 10-3 | 1.805 6 | |
| 32 | 1.157 5 × 10-3 | 2.269 6 | 1.633 2 × 10-3 | 1.935 4 | |
| 64 | 1.994 9 × 10-4 | 2.536 6 | 3.606 0 × 10-4 | 2.179 2 | |
| 1.5 | 4 | 6.448 4 × 10-2 | 6.442 7 × 10-2 | ||
| 8 | 2.184 1 × 10-2 | 1.561 9 | 2.192 5 × 10-2 | 1.555 1 | |
| 16 | 6.174 5 × 10-3 | 1.822 6 | 6.359 5 × 10-3 | 1.785 6 | |
| 32 | 1.508 5 × 10-3 | 2.033 2 | 1.746 7 × 10-3 | 1.864 3 | |
| 64 | 2.393 2 × 10-4 | 2.656 1 | 4.619 3 × 10-4 | 1.918 9 |
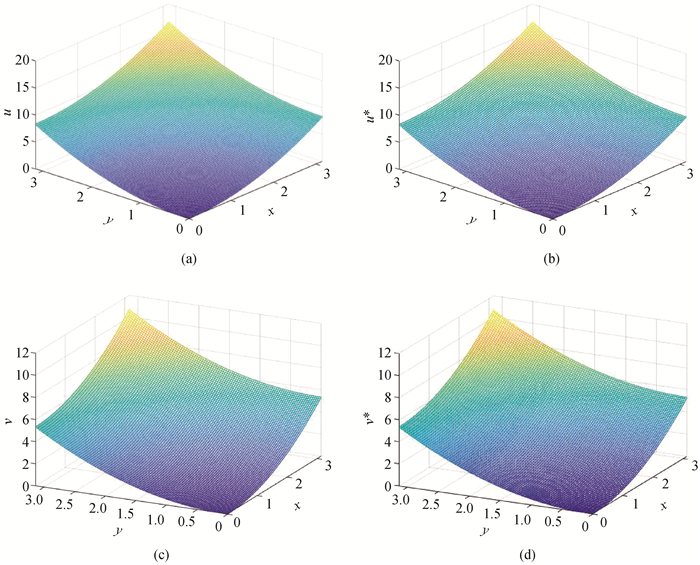
Fig.2 Evolution of exact solutions and LBM numerical solutions (a) exact solution of u; (b) numerical solution of u; (c) exact solution of v; (d) numerical solution of v
| T | α=1.1 | α=1.3 | α=1.5 | α=1.7 | α=1.9 |
| 0.2 | 5.826 5 × 10-4 | 5.879 4 × 10-4 | 5.958 1 × 10-4 | 6.088 1 × 10-4 | 6.329 9 × 10-4 |
| 0.4 | 5.136 5 × 10-4 | 5.243 1 × 10-4 | 5.400 8 × 10-4 | 5.660 8 × 10-4 | 6.144 6 × 10-4 |
| 0.6 | 4.285 4 × 10-4 | 4.445 7 × 10-4 | 4.681 5 × 10-4 | 5.069 4 × 10-4 | 5.792 2 × 10-4 |
| 0.8 | 3.266 8 × 10-4 | 3.481 1 × 10-4 | 3.794 1 × 10-4 | 4.307 6 × 10-4 | 5.265 5 × 10-4 |
| 1.0 | 2.515 0 × 10-4 | 2.608 2 × 10-4 | 2.818 1 × 10-4 | 3.364 5 × 10-4 | 4.562 3 × 10-4 |
Table 3 Global relative error at different time under different α
| T | α=1.1 | α=1.3 | α=1.5 | α=1.7 | α=1.9 |
| 0.2 | 5.826 5 × 10-4 | 5.879 4 × 10-4 | 5.958 1 × 10-4 | 6.088 1 × 10-4 | 6.329 9 × 10-4 |
| 0.4 | 5.136 5 × 10-4 | 5.243 1 × 10-4 | 5.400 8 × 10-4 | 5.660 8 × 10-4 | 6.144 6 × 10-4 |
| 0.6 | 4.285 4 × 10-4 | 4.445 7 × 10-4 | 4.681 5 × 10-4 | 5.069 4 × 10-4 | 5.792 2 × 10-4 |
| 0.8 | 3.266 8 × 10-4 | 3.481 1 × 10-4 | 3.794 1 × 10-4 | 4.307 6 × 10-4 | 5.265 5 × 10-4 |
| 1.0 | 2.515 0 × 10-4 | 2.608 2 × 10-4 | 2.818 1 × 10-4 | 3.364 5 × 10-4 | 4.562 3 × 10-4 |
| T | β=1.1 | β=1.3 | β=1.5 | β=1.7 | β=1.9 |
| 0.2 | 9.453 0 × 10-5 | 8.199 4 × 10-5 | 6.534 1 × 10-5 | 4.626 4 × 10-5 | 5.141 0 × 10-5 |
| 0.4 | 2.472 2 × 10-4 | 2.223 3 × 10-4 | 1.874 1 × 10-4 | 1.381 9 × 10-4 | 1.089 5 × 10-4 |
| 0.6 | 4.791 8 × 10-4 | 4.402 4 × 10-4 | 3.854 3 × 10-4 | 3.014 4 × 10-4 | 2.041 9 × 10-4 |
| 0.8 | 8.382 4 × 10-4 | 7.826 8 × 10-4 | 7.034 6 × 10-4 | 5.804 2 × 10-4 | 3.912 8 × 10-4 |
| 1.0 | 1.444 3 × 10-3 | 1.366 5 × 10-3 | 1.252 1 × 10-3 | 1.077 8 × 10-3 | 7.732 5 × 10-4 |
Table 4 Global relative error at different time under different β
| T | β=1.1 | β=1.3 | β=1.5 | β=1.7 | β=1.9 |
| 0.2 | 9.453 0 × 10-5 | 8.199 4 × 10-5 | 6.534 1 × 10-5 | 4.626 4 × 10-5 | 5.141 0 × 10-5 |
| 0.4 | 2.472 2 × 10-4 | 2.223 3 × 10-4 | 1.874 1 × 10-4 | 1.381 9 × 10-4 | 1.089 5 × 10-4 |
| 0.6 | 4.791 8 × 10-4 | 4.402 4 × 10-4 | 3.854 3 × 10-4 | 3.014 4 × 10-4 | 2.041 9 × 10-4 |
| 0.8 | 8.382 4 × 10-4 | 7.826 8 × 10-4 | 7.034 6 × 10-4 | 5.804 2 × 10-4 | 3.912 8 × 10-4 |
| 1.0 | 1.444 3 × 10-3 | 1.366 5 × 10-3 | 1.252 1 × 10-3 | 1.077 8 × 10-3 | 7.732 5 × 10-4 |
| Δt | GRE(N, M, Δt, u) | Order2(u) | GRE(N, M, Δt, v) | Order2(v) |
| 0.1 | 4.619 0 × 10-2 | 5.383 5 × 10-2 | ||
| 0.05 | 2.331 0 × 10-2 | 0.986 6 | 2.483 8 × 10-2 | 1.116 0 |
| 0.025 | 1.151 5 × 10-2 | 1.017 4 | 1.138 3 × 10-2 | 1.125 7 |
| 0.012 5 | 5.532 6 × 10-3 | 1.057 5 | 4.972 5 × 10-3 | 1.194 8 |
| 0.006 25 | 2.573 0 × 10-3 | 1.104 5 | 1.984 2 × 10-3 | 1.325 4 |
Table 5 Global relative error and convergence rate at different time steps
| Δt | GRE(N, M, Δt, u) | Order2(u) | GRE(N, M, Δt, v) | Order2(v) |
| 0.1 | 4.619 0 × 10-2 | 5.383 5 × 10-2 | ||
| 0.05 | 2.331 0 × 10-2 | 0.986 6 | 2.483 8 × 10-2 | 1.116 0 |
| 0.025 | 1.151 5 × 10-2 | 1.017 4 | 1.138 3 × 10-2 | 1.125 7 |
| 0.012 5 | 5.532 6 × 10-3 | 1.057 5 | 4.972 5 × 10-3 | 1.194 8 |
| 0.006 25 | 2.573 0 × 10-3 | 1.104 5 | 1.984 2 × 10-3 | 1.325 4 |
| T | GRE(N, M, Δt, u) | GRE(N, M, Δt, v) |
| 0.2 | 7.215 3 × 10-4 | 8.208 9 × 10-5 |
| 0.4 | 7.928 4 × 10-4 | 1.455 0 × 10-4 |
| 0.6 | 8.474 5 × 10-4 | 2.153 3 × 10-4 |
| 0.8 | 8.894 6 × 10-4 | 3.465 4 × 10-4 |
| 1 | 9.254 5 × 10-4 | 6.966 4 × 10-4 |
Table 6 Global relative error(GRE) at different moments(T)
| T | GRE(N, M, Δt, u) | GRE(N, M, Δt, v) |
| 0.2 | 7.215 3 × 10-4 | 8.208 9 × 10-5 |
| 0.4 | 7.928 4 × 10-4 | 1.455 0 × 10-4 |
| 0.6 | 8.474 5 × 10-4 | 2.153 3 × 10-4 |
| 0.8 | 8.894 6 × 10-4 | 3.465 4 × 10-4 |
| 1 | 9.254 5 × 10-4 | 6.966 4 × 10-4 |
| 1 |
DOI |
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
DOI |
| 6 |
|
| 7 |
DOI |
| 8 |
DOI |
| 9 |
|
| 10 |
DOI |
| 11 |
DOI |
| 12 |
DOI |
| 13 |
DOI |
| 14 |
DOI |
| 15 |
DOI |
| 16 |
DOI |
| 17 |
DOI |
| 18 |
DOI |
| 19 |
DOI |
| 20 |
何雅玲, 王勇, 李庆. 格子Boltzmann方法的理论及应用[M]. 北京: 科学出版社, 2009: 1- 237.
|
| 21 |
郭照立, 郑楚光, 李青, 等. 流体动力学的格子Boltzmann方法[M]. 武汉: 湖北科学技术出版社, 2002: 1- 166.
|
| 22 |
DOI |
| 23 |
DOI |
| 24 |
DOI |
| 25 |
DOI |
| 26 |
DOI |
| 27 |
DOI |
| 28 |
|
| 29 |
DOI |
| 30 |
DOI |
| 31 |
|
| 32 |
|
| 33 |
李梦军, 戴厚平, 魏雪丹, 等. 空间分数阶电报方程的格子Boltzmann方法[J]. 应用数学和力学, 2021, 42 (5): 522- 530.
|
| 34 |
DOI |
| 35 |
DOI |
| 36 |
DOI |
| [1] | Liubin ZHANG, Yanguang SHAN, Zhicheng RONG. Single Bubble Dynamics in Pool Boiling Under Uniform Electric Field: LBM Simulation [J]. Chinese Journal of Computational Physics, 2022, 39(5): 537-548. |
| [2] | Jiaxin LIU, Lin ZHENG, Beihao ZHANG. Entropy Generation in Double-diffusive Natural Convection in a Square Porous Enclosure: Lattice Boltzmann Method [J]. Chinese Journal of Computational Physics, 2022, 39(5): 549-563. |
| [3] | Pin-liang LIN, Huan-huan FENG, Yu-hong DONG. Analysis of Flow Field Around a Cylinder with Porous Media Layer [J]. Chinese Journal of Computational Physics, 2022, 39(4): 418-426. |
| [4] | Qiao-ling ZHANG, He-fang JING. Flow Patterns in Three-dimensional Lid-driven Cavities with Curved Boundary: MRT-LBM Study [J]. Chinese Journal of Computational Physics, 2022, 39(4): 427-439. |
| [5] | Lu CHEN, Ming GAO, Jia LIANG, Dongmin WANG, Yugang ZHAO, Lixin ZHANG. Droplet Upward Movement on an Inclined Surface Under Wetting Gradient: Lattice Boltzmann Simulation [J]. Chinese Journal of Computational Physics, 2021, 38(6): 672-682. |
| [6] | Xuedan WEI, Houping DAI, Mengjun LI, Zhoushun ZHENG. Lattice Boltzmann Method for One-dimensional Riesz Spatial Fractional Convection-Diffusion Equations [J]. Chinese Journal of Computational Physics, 2021, 38(6): 683-692. |
| [7] | Jiangtao ZHENG, Ninghong JIA, Huifang HU, Yong YANG, Yang JU, Moran WANG. Study on Liquid-Liquid Spontaneous Imbibition Dynamics in Bifurcated Channels [J]. Chinese Journal of Computational Physics, 2021, 38(5): 543-554. |
| [8] | Qin LOU, Sheng TANG, Haoyuan WANG. Numerical Simulation of Bubble Dynamics in Porous Media with a Lattice Boltzmann Large Density Ratio Model [J]. Chinese Journal of Computational Physics, 2021, 38(3): 289-300. |
| [9] | Jia LIANG, Ming GAO, Lu CHEN, Dongmin WANG, Lixin ZHANG. Lattice Boltzmann Study of a Droplet Impinging on a Stationary Droplet on a Fixed Wall Surface with Different Wettability [J]. Chinese Journal of Computational Physics, 2021, 38(3): 313-323. |
| [10] | YUAN Junjie, YE Xin, SHAN Yanguang. Natural Convection in Triangular Cavity Filled with Nanofluid: Lattice Boltzmann Simulation [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2021, 38(1): 57-68. |
| [11] | ZHAO Ming, WANG Ke, YU Duanmin. Ruelle-Takens Chaotic Natural Convection in a Horizontal Annulus with an Internally Slotted Circle [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(6): 667-676. |
| [12] | WANG Jianyi, PAN Zhenhai, WU Huiying. Numerical Study of Inertial Focusing Behavior of Ellipsoidal Particles in a Microchannel [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(6): 677-686. |
| [13] | TANG Guyue, LOU Qin, LI Ling. Influence of Heating Size and Rayleigh Number on Natural Convection in a Deformable Open Cavity:Lattice Boltzmann Method [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(3): 263-276. |
| [14] | HU Yu, SUN Tao. Three-dimensional Numerical Simulation of Dynamics Characteristics of Two Rising Bubbles with Lattice Boltzmann Method [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(3): 277-283. |
| [15] | LIAN Xiaolong, CHEN Yue, LI Peisheng, ZHANG Ying, LI Wei, LIU Qiang. Numerical Study of Droplet Impact Liquid Film with MRT-LB Pseudo-potential Model [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(1): 79-87. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||
Copyright © Chinese Journal of Computational Physics
E-mail: jswl@iapcm.ac.cn
Supported by Beijing Magtech Co., Ltd.
