Since a quantum system is inevitably influenced by some unpredictable perturbations, we thereby conclude that all the experimental realizations of Grover quantum search algorithm reported were, in fact, achieved in a three-dimensional complex subspace. We also prove that in a two-dimensional complex subspace, for any given initial superposition of basis states|γ₀>=cosβ₀|α>+sinβ₀e^iζ|β)(β₀ is a small positive real number, ζ is an arbitrary real number), there exists a set of solutions F_j={(θ_j,θ_j-1,…,θ₁),(φ_j,φ_j-1,…,φ₁)} such that a desired state can be found with certainty for some positive integer j≥2, where the phase rotation angles θ_l andθ_t are real numbers but not equal to 2k'π,1 ≤ 1 ≤ j,k'is an arbitrary integer. 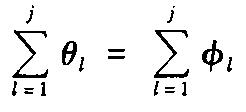If it is only required that a desired state can be found with high success probability, then as the total number of the desired and undesired states in an unsorted database is sufficiently large the above set of solutions F_j can be written in the form  for a relatively small positive integer j.