Archive

25 December 1987, Volume 4 Issue 4 Previous Issue    Next Issue

---

For Selected:

Download Citations EndNote Ris BibTeX

Toggle Thumbnails

Select

A NUMERICAL STUDY OF THE FERMI SURFACE INSIDE A BRILLOUIN ZONE CORNER Cheng Kai-jia, Kao Zhan-peng, Fan Qi-ke 1987, 4(4): 389-400.  Abstract ( )   PDF (653KB) ( )   The present paper presents a numerical study of the Fermi surface near and inside a Brillouin zone corner in a conducting band. Both the periodic lattice potential and mutual jnteractions among electrons are taken into account. For concreteness and illustration, the computation was carried out on the metallic aluminum on its first Brillouin zone corner. The parameters of the potential are from the calculated results of Heine. The main results obtained are as follows:The shape of the Fermi surface are far from spherical, being protruding in central part of the solid angle of the zone corner,and gradually smoothes down as the layers of electrons forming the Fermi surface are continually added; there exists a minimum of the electron energy in the continual addition of layers of extraneous electrons and thereafter the energy of electrons increases rapidly; the number of the electron density reaches about 1018/cm3.An estimation of the magnitude of exchange energy shows that.a decrease of the exchange energy about one third for the electrons from different zone corners as compared with that inside a same corner. This will give rise to a broken symmetry in the distribution of electron currents. Further investigation of the problem seems necessary in view of the direct contradiction to the Bloch's theorem of ground states without a permanent current.

Select

A NUMERICAL METHOD FOR TWO-DIMENSIONAL ANISOTROPIC TRANSPORT PROBLEM IN CYLINDRICAL GEOMETRY Du Ming-sheng, Feng Tie-kai, Fu Lian-xiang, Cao Chang-shu, Liu Yu-Lan 1987, 4(4): 401-412.  Abstract ( )   PDF (628KB) ( )   We deal with the triangular mesh-discontinuous finite element method for solving the time-dependent anisotropic neutron transport problem in two-dimensional cylindrical geometry. A priori estimate of the numerical solution is given. Stability is proved. We have computed a two dimensional anisotropic neutron transport problem and a Tungsten-Carbide critical assembly problem by using the numerical method. In comparision with DSN method and the experiments the method is satisfactory.

Select

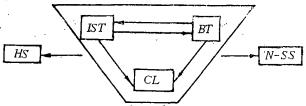
REIATIONSHIPS AMONG THE FIVE CHARACTERISTICS FOR A CLASS OF NOLINEAR WAVE EQUATIONS Huang Lei-de 1987, 4(4): 413-425.  Abstract ( )   PDF (629KB) ( )   We make use of the K-dv equation to clarify the relation-shios among the five characteristics for a class of nonlinear wave equatioos.It is shown that (1) Inverse scatering transform (IST);(2) Böcklund transformation (BT);(3)N-soliton solutions (N-SS);(4)a unite or an infinite number of conservation laws (CL) and (5)a complete integrable Hamilton system (HS) are closely related.The scheme of the presentation is shown in the following figure

Select

THE FINITE ANALYTIC METHOD OF UNSTEADY ONE-DIMENSIONAL CONVECTIVE TRANSPORT EQUATIONS Zeng Xiang-jin, Li Wei 1987, 4(4): 426-438.  Abstract ( )   PDF (625KB) ( )   This paper introduees the finite analytic method, then gives a few results of the finite analytic method for unsteady one-dimensional convective transport equations. An example showing effictiveness of FAM is given.

Select

THE SUFFICIENT AND NECESSARY CONDITIONS FOR MCS WITH PERIOD m FOR GIVEN MODUL M Li Feng-lin 1987, 4(4): 439-445.  Abstract ( )   PDF (418KB) ( )   The author presended the sufficient and necessary Conditions for MCS With maximum-period δ(M) for given modul M in[1]. In this paper, the result in[1] is extended to any period m(≤δ(M)). At last, an example verifies the correctness of the conclusions given in this paper.

Select

THE CHARACTERISTIC FINITE ANALYTIC METHOD FOR THE NUMERICAL SOLUTION OF CONVECTIVE DIFFUSION EQUATION Sun Yu-Ping 1987, 4(4): 446-458.  Abstract ( )   PDF (688KB) ( )   A characteristic finite analytic method is proposed to obtain the numeri cal solution of convective diffusion eguation. The scheme formed is unconditionally L∞ stable and in accordance with the convective diffusion phenomenon in physics.In this paper the existence and uniqueness of the scheme is proved and the error estimate of the numerical solution for the linear and non-linear equation is given. The numevical experiment shows that the present method has the ability to simulate the convective diffusion equation with high order accuracy, Irttle numerical dissipation, perfect stability and without any parasitic osillation.

Select

A FINITE ELEMENT METHOD OF TRIANGULAR DIVISION FOR NUMERICAL SIMULATION OF TWO DIMENSIONAL AND TWO PHASE FLOW Zhang Zi-xiang, Qu De-bin, Chu Zhong-wu 1987, 4(4): 459-468.  Abstract ( )   PDF (529KB) ( )   Int his paper, a finite element method of triongular division is presented for a two dimensional-and two phase (oil and water) nonlinear model in reservoir.Authors designed associated computer program, gave the saturation distribution during oil production with the data in Daqing oil field in connetion with IBM-PC/XT computer, and predicted the break through time with satisfactory results.On the basis of theoretical analysis and the results the finite element method was compared with the finite elent method of rectangular division and the finite difference method.

Select

PHYSICS DESIGN FOR THE γ-RAY THICKNESSIVSETER Feng Zheng-yong, Xiao Chen-guo, Li Yin-hua, Shi Guo-shun 1987, 4(4): 469-479.  Abstract ( )   PDF (659KB) ( )   In this article, the attenuation of broad beam of γ-ray passing through a medium has been researched with Monte-Carlo method and it was pointed out that the beam obeys the exponential rule if an equivalent absorption coefficient is used. A new idea of design forγ-ray thicknessmeter was then advanced for weakening radiation intensity, increasing count, and improving measurement precision. An absorption experiment of broad beam of γ-ray with energy of 60 keV in aluminium has been done and the result agrees with Monte-Carlo calculation.

Select

THE THEOREM OF COMPOSITION OF ACCELERATION IN THE MOVING SYSTEM OF COORDINATES OF PLANE MOTION Wang Li-Zhong 1987, 4(4): 480-488.  Abstract ( )   PDF (421KB) ( )   Different textbooks of Mechanics give solely composition of accelerations where motion of moving frame of coordinates is rotation about a fixed axis and translation. This paper has developed the Theorem of Composition of Accelerations of Moving frame in plane Motion. We obtain a set of differ-antial equations which are available to be solved on digital computer.

Select

EXACT SOLUTIONS FOR VERTICAL INTERFERENCE IN HETEROGENEOUS DOUBLE POROUS MEDIA SEPARATED BY A LAYER OF LOW PERMEABILITY Feng Wen-guang 1987, 4(4): 489-502.  Abstract ( )   PDF (691KB) ( )   Two mathematical models are developed in this paper that describe fluid flow and pressure behavior in a porous medium reservoir and double porous media reservoir consisting of two permeable zones separated by a zone of low permeability, or a "tight zone".Their solutions are obtained which are the exact solutions and the long time asymptotic solutions in infinite formation.The solutions are used to design and to interpret buildup curves,vertical interference tests and vertical pules tests of oil field in a single well or multiple wells for the porous medium and the double porous media.

Select

A FILTERING STEP BY STEP METHOD FOR OBTAINING THE EXTERNAL SOLUTION OF PLASMA EQUILIBRIUM Luo Zheng-ming, Feng Gui-yun 1987, 4(4): 503-512.  Abstract ( )   PDF (605KB) ( )   By combining the filtering procedure and the usual step by step method, a numerical method that can solve improperly posed Cauchy problem of the flux function equation for plasma equilibrium, has been obtained. By the new method, the drastic instability appearing in the usual step by step calculation, which was unsuccessfully applied to the calculation of the external flux function, has been overcome, and the stable numerical results have been obtained.