基于LBM的均匀电场池沸腾单气泡动力学模拟

doi:10.19596/j.cnki.1001-246x.8475

摘要/Abstract

摘要：

采用格子玻尔兹曼方法(LBM), 在气-液相变模型的基础上, 耦合理想电介质模型, 模拟均匀电场作用下池沸腾单气泡成核、生长、脱离过程, 详细研究重力加速度和电场强度对气泡动力学的影响。结果表明: 在重力加速度相同的情况下, 随着电场强度的增加, 气泡的脱离直径与脱离时间随之减小, 壁面平均热流增加。随着重力加速度减小, 壁面平均热流减少, 电场强度对于气泡脱离频率的影响更加显著。气泡在均匀电场中形状发生改变, 它将沿着电场线的方向拉伸, 变得更加细长, 电场强度与气泡的纵横比和高度呈线性相关。

关键词: 格子玻尔兹曼方法, 池沸腾, 均匀电场, 气泡动力学

Abstract:

Lattice Boltzmann method (LBM) is used in a coupled perfect dielectric model and liquid-vapor phase-change model to simulate nucleation, growth, and separation process of a single bubble in pool boiling under uniform electric field. Effects of gravitational acceleration and electric field on bubble dynamics are studied in detail. It shows that under same gravitational acceleration, with the increase of electric field intensity, the bubble departure diameter decreases and the bubble release frequency increases, and the averaged wall heat flux increases. With the decrease of gravitational acceleration, the averaged wall heat flux decreases as well, and the electric field has significant influence on the bubble release frequency. In addition, the bubble deforms in a uniform electric field, and it stretches along the direction of electric field to become slender. The electric field intensity is linearly related to the aspect ratio and height of the bubble.

Key words: lattice Boltzmann method, pool boiling, uniform electric field, bubble dynamics

张浏斌, 单彦广, 戎志成. 基于LBM的均匀电场池沸腾单气泡动力学模拟[J]. 计算物理, 2022, 39(5): 537-548.

Liubin ZHANG, Yanguang SHAN, Zhicheng RONG. Single Bubble Dynamics in Pool Boiling Under Uniform Electric Field: LBM Simulation[J]. Chinese Journal of Computational Physics, 2022, 39(5): 537-548.

图/表 17

图1 计算区域示意图

Fig.1 A schematic of the computation domain

图2 静态接触角和gs的关系

Fig.2 Relation between static contact angle and gs

图3 等效直径与实验结果

Fig.3 Equivalent diameter and experimental results

图4 单气泡生长和脱离的数值结果和实验

Fig.4 Numerical results and experimental observations of single bubble growth and departure

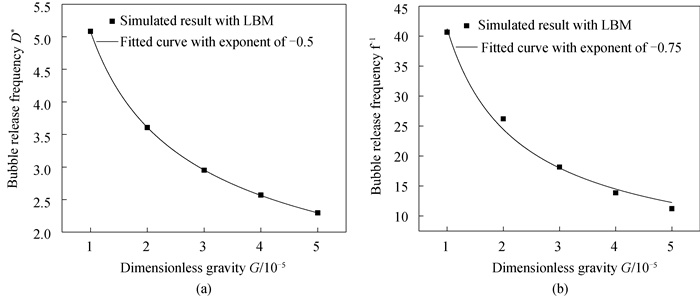
图5 重力加速度与气泡脱离直径、脱离周期的关系(a) 脱离直径; (b)脱离时间

Fig.5 Relations between gravity and bubble separation diameter and separation time (a) separation diameter, (b) separation time

图6 电场强度与电场流线分布

Fig.6 Distribution of electric field intensities and electric field streamlines

图7 电场强度分布(a) y=2.5D0; (b) x=2.5D0

Fig.7 Distributions of electric field intensities at (a) y=2.5D0; (b) x=2.5D0

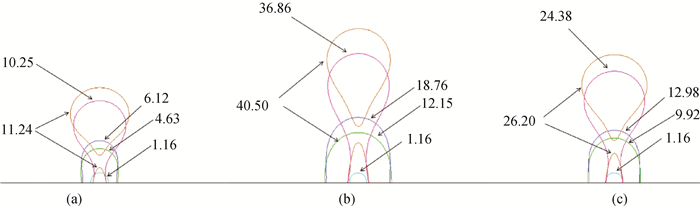
图8 无电场时不同重力加速度下气泡轮廓(a) G = 0.00005; (b) G = 0.00001; (c) G = 0.00002

Fig.8 Evolutions of bubble contour under different gravitational accelerations without electric field (a) G = 0.00005; (b) G = 0.00001; (c) G = 0.00002

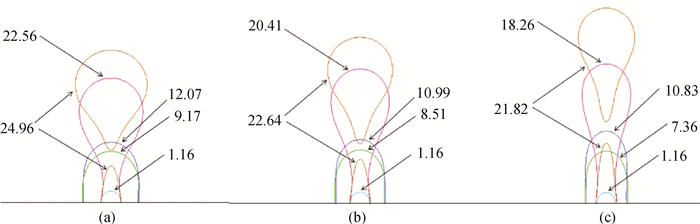
图9 G = 0.00002时，不同电场强度下池沸腾气泡轮廓的演变(a) V0=10; (b)V0=20; (c)V0=30

Fig.9 Evolutions of bubble contour during pool boiling under different electric field intensities as G = 0.00002 (a) V0=10; (b) V0=20; (c)V0=30

图10 电场力分布

Fig.10 Electric field force distribution

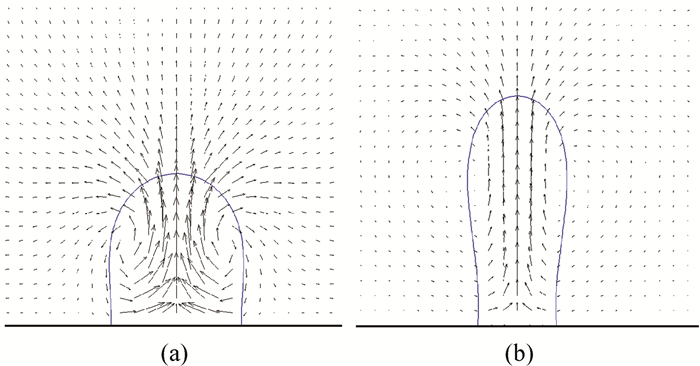
图11 G = 0.00002时池沸腾气泡周围速度矢量分布(a) V0=0; (b) V0=30

Fig.11 Distributions of velocity vectors around a vapor bubble during pool boiling at G = 0.00002 (a) V0=0; (b) V0=30

图12 不同重力加速度下，电场强度对气泡脱离直径的影响

Fig.12 Effect of electric field intensity on bubble departure diameter under different gravitational accelerations

图13 不同重力加速度下，电场强度对气泡脱离时间的影响

Fig.13 Effect of electric field intensity on bubble release frequency under different gravitational accelerations

图14 气泡纵横比

Fig.14 Aspect ratio of bubble

图15 不同电场强度下气泡高度和纵横比随时间变化(a) 纵横比; (b) 高度

Fig.15 Effect of electric field intensity on the evolution of bubble height and AR (a) AR; (b) height

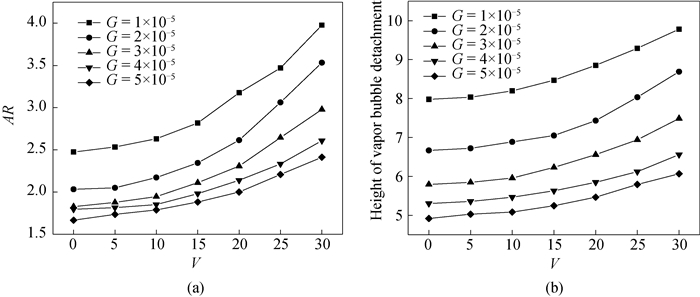
图16 不同重力加速度下，气泡脱离时纵横比和高度随着电场强度变化(a) 纵横比; (b) 高度

Fig.16 Effect of electric field intensity on bubble detachment height and AR under different gravitational acceleration (a) AR; (b) height

图17 不同电场强度下，壁面平均热流随着重力加速度的变化

Fig.17 Average wall heat flux as functions of acceleration of gravity under different electric field intensity

参考文献 30

1	LANBARAN D A , TAQIZADEH R , ESMAILZADEH E , et al. Experimental investigation on pair bubble columns under high voltage DC electric filed[J]. Journal of Electrostatics, 2020, 106 (7): 103456.
2	GAO M , CHENG P , QUAN X . An experimental investigation on effects of an electric field on bubble growth on a small heater in pool boiling[J]. International Journal of Heat and Mass Transfer, 2013, 67, 984- 991. DOI
3	SCHWEIZER N , DI MARCO P , STEPHAN P . Investigation of wall temperature and heat flux distribution during nucleate boiling in the presence of an electric field and in variable gravity[J]. Experimental Thermal and Fluid Science, 2013, 44, 419- 430. DOI
4	DONG W , LI R Y , YU H L , et al. An investigation of behaviours of a single bubble in a uniform electric field[J]. Experimental Thermal and Fluid Science, 2006, 30 (6): 579- 586. DOI
5	PENG Y , CHEN F , SONG Y , et al. Single bubble behavior in direct current electric field[J]. Chinese Journal of Chemical Engineering, 2008, 16 (2): 178- 183. DOI
6	DONG Z, CHENG D, LI R, et al. Experimental study of influence on bubble in electric field[C]//2011 International Conference on Materials for Renewable Energy & Environment, 2011, 2(1): 1280-1283.
7	LIN Y . Two-phase electro-hydrodynamic flow modeling by a conservative level set model[J]. Electrophoresis, 2013, 34 (5): 736- 744. DOI
8	PANDEY V , BISWAS G , DALAL A . Saturated film boiling at various gravity levels under the influence of electrohydrodynamic forces[J]. Physics of Fluids, 2017, 29 (3): 032104. DOI
9	PANDEY V , BISWAS G , DALAL A . Effect of superheat and electric field on saturated film boiling[J]. Physics of Fluids, 2016, 28 (5): 052102. DOI
10	ZHU C-S , HAN D , XU S . Phase field simulation of single bubble behavior under an electric field[J]. Chinese Physics B, 2018, 27 (9): 393- 399.
11	GONG S , CHENG P . A lattice Boltzmann method for simulation of liquid-vapor phase-change heat transfer[J]. International Journal of Heat and Mass Transfer, 2012, 55 (17-18): 4923- 4927. DOI
12	龚帅, 张朝阳, 郑平. 池沸腾传热的LBM直接数值模拟及加热器热响应[J]. 工程热物理学报, 2019, 40 (01): 137- 144.
13	LI Q , KANG Q J , FRANCOIS M M , et al. Lattice Boltzmann modeling of boiling heat transfer: The boiling curve and the effects of wettability[J]. International Journal of Heat and Mass Transfer, 2015, 85, 787- 796. DOI
14	CHANG X , HUANG H , CHENG Y P , et al. Lattice Boltzmann study of pool boiling heat transfer enhancement on structured surfaces[J]. International Journal of Heat and Mass Transfer, 2019, 139, 588- 599. DOI
15	YUAN J , WENG Z , SHAN Y . Modelling of double bubbles coalescence behavior on different wettability walls using LBM method[J]. International Journal of Thermal Sciences, 2021, 168, 107037. DOI
16	YUAN J , YE X , SHAN Y . Modeling of the bubble dynamics and heat flux variations during lateral coalescence of bubbles in nucleate pool boiling[J]. International Journal of Multiphase Flow, 2021, 142, 103701. DOI
17	SUN T , LIU Z , FAN W , et al. Three-dimensional numerical simulation of vapor bubble rising in superheated liquid by lattice Boltzmann method[J]. Chinese Journal of Computational Physics, 2019, 36 (6): 659- 664.
18	HU Y , SUN T . Three-dimensional numerical simulation of dynamics characteristics of two rising bubbles with lattice Boltzmann method[J]. Chinese Journal of Computational Physics, 2020, 37 (3): 277- 283.
19	LOU Q , TANG S , WANG H . Numerical simulation of bubble dynamics in porous media with a lattice Boltzmann large density ratio model[J]. Chinese Journal of Computational Physics, 2021, 38 (3): 289- 300.
20	GONG S , CHENG P . Lattice Boltzmann simulation of periodic bubble nucleation, growth and departure from a heated surface in pool boiling[J]. International Journal of Heat and Mass Transfer, 2013, 64, 122- 132. DOI
21	HE X Y , LI N . Lattice Boltzmann simulation of electrochemical systems[J]. Computer Physics Communications, 2000, 129 (1-3): 158- 166. DOI
22	ZHAO W, ZHANG Y, XU B, et al. Pseudopotential multiple-relaxation-time lattice Boltzmann simulation of vapor condensation on vertical subcooled walls[J]. arXiv preprint arXiv: 180804973, 2018.
23	曾建邦, 李隆键, 廖全, 等. 池沸腾中气泡生长过程的格子Boltzmann方法模拟[J]. 物理学报, 2011, 60 (6): 520- 529.
24	SON G , DHIR V K , RAMANUJAPU N . Dynamics and heat transfer associated with a single bubble during nucleate boiling on a horizontal surface[J]. Journal of Heat Transfer, 1999, 121 (3): 623- 631. DOI
25	MUKHERJEE A , DHIR V K . Study of lateral merger of vapor bubbles during nucleate pool boiling[J]. Journal of Heat Transfer, 2004, 126 (6): 1023- 1039. DOI
26	FRITZ W . Maximum volume of vapor bubbles[J]. Physik Zeitschr, 1935, 36, 379- 384.
27	ZUBER N . Nucleate boiling: The region of isolated bubbles and the similarity with natural convection[J]. International Journal of Heat and Mass Transfer, 1963, 6 (1): 53- 78. DOI
28	FENG Y , LI H , GUO K , et al. Numerical investigation on bubble dynamics during pool nucleate boiling in presence of a non-uniform electric field by LBM[J]. Applied Thermal Engineering, 2019, 155, 637- 649. DOI
29	易天浩, 陈超越, 雷作胜, 等. 微重力池沸腾中的气泡和传热行为数值模拟[J]. 空间科学学报, 2019, 39 (4): 469- 477.
30	FENG Y , LI H X , GUO K K , et al. Numerical study of single bubble growth on and departure from a horizontal superheated wall by three-dimensional lattice Boltzmann method[J]. Microgravity Science & Technology, 2018, 30 (6): 761- 773.

[1]	郑江韬, 贾宁洪, 胡慧芳, 杨勇, 鞠杨, 王沫然. 分支通道内液-液自发渗吸规律研究[J]. 计算物理, 2021, 38(5): 543-554.
[2]	娄钦, 汤升, 王浩原. 基于格子Boltzmann大密度比模型的多孔介质内气泡动力学行为数值模拟[J]. 计算物理, 2021, 38(3): 289-300.
[3]	王子墨, 李凌. 超短激光打孔中快速相变的格子玻尔兹曼模拟[J]. 计算物理, 2020, 37(3): 299-306.
[4]	连小龙, 陈岳, 李培生, 张莹, 李伟, 刘强. 基于MRT-LB伪势模型的液滴撞击液膜数值研究[J]. 计算物理, 2020, 37(1): 79-87.
[5]	罗祝清, 娄钦, 徐洪涛, 杨茉. 热质双扩散与流固共轭传热及吸附的LBM模拟[J]. 计算物理, 2019, 36(1): 60-68.
[6]	周天, 李学敏, 刘峰. 二维平板间驻波声流的MRT-LBM数值研究[J]. 计算物理, 2018, 35(1): 39-46.
[7]	张东辉, 刘方贵, 张金存, 芮孝芳. 应用于非线性热传导方程的格子玻尔兹曼方法[J]. 计算物理, 2010, 27(5): 699-704.
[8]	陈瑜, 夏振华, 蔡庆东. 基于树网格的格子Boltzmann方法以及曲线边界的处理[J]. 计算物理, 2010, 27(1): 23-30.
[9]	聂小波. 激波的格子玻尔兹曼方法模拟[J]. 计算物理, 1998, 15(1): 1-5.