可压缩黏性圆射流稳定性分析

doi:10.19596/j.cnki.1001-246x.8479

摘要/Abstract

摘要：

基于线性稳定性理论, 得到空间模式下的可压缩黏性液体圆射流自由表面扰动发展的色散方程, 并对色散方程进行验证。研究表明: 液体可压缩性在射流的分裂与雾化过程中所起到的不稳定作用很小, 随着液体马赫数的增大, 扰动波的最大增长率基本不变; 气体可压缩性对射流的不稳定作用随气体马赫数的增大而增大。黏滞力和表面张力对射流的稳定作用分别随雷诺数和韦伯数的增大逐渐减小; 气动力对射流的不稳定作用随气液密度比的增大基本不变。

关键词: 射流, 可压缩, 流动稳定性, 色散方程, 分裂与雾化

Abstract:

Mechanism of splitting and atomization of compressible viscous 。ular jet was studied with linear stability theory. The dispersion equation for disturbance development of liquid jet surface in space mode was obtained and verified. It shows that the influence of liquid compressibility on instability of liquid jet is very small. With the increase of Mach number of liquid, the maximum growth rate of disturbance wave is basically unchanged. Effect of gas compressibility on jet stability increases with the increase of gas Mach number. With the increase of Reynolds number and Weber number, the effect of viscous force and surface tension on jet stability decreases gradually. With the increase of gas-liquid density ratio, the effect of aerodynamic force on jet stability is basically unchanged.

Key words: liquid jet, compressible, flow stability, dispersion equation, splitting and atomization

张华, 杨明慧. 可压缩黏性圆射流稳定性分析[J]. 计算物理, 2022, 39(5): 529-536.

Hua ZHANG, Minghui YANG. Stability Analysis of Compressible Viscous Circular Jet[J]. Chinese Journal of Computational Physics, 2022, 39(5): 529-536.

图/表 6

图1 射流示意图

Fig.1 Jet diagram

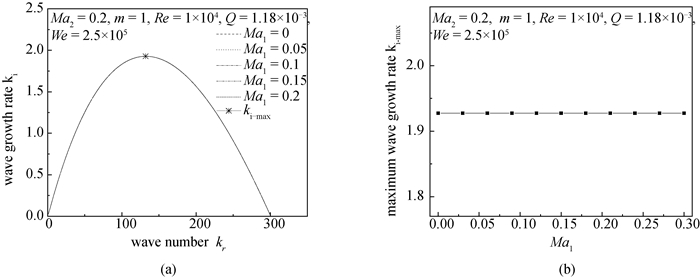
图2 液体马赫数Ma1对扰动波增长率的影响(a)波数kr-扰动波增长率ki；(b)液体马赫数Ma1-最大扰动波增长率ki-max

Fig.2 Influence of liquid Mach number Ma1 on the growth rate of disturbance wave (a) Wave number kr- Disturbance wave growth rate ki; (b) Ma1 - Maximum disturbance wave growth rate ki-max

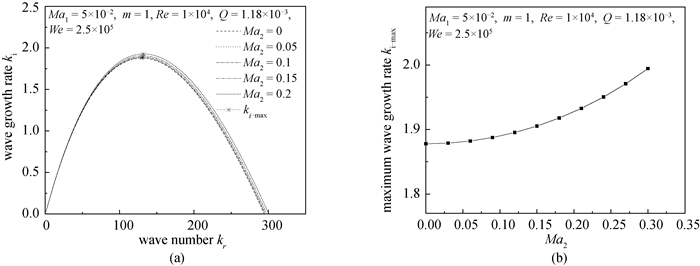
图3 气体马赫数Ma2对扰动波增长率的影响(a)波数kr-扰动增长率ki；(b)气体马赫数Ma2-最大扰动增长率ki-max

Fig.3 Influence of Mach number Ma2 on the growth rate of disturbance wave (a) Wave number kr-Disturbance wave growth rate ki; (b) Ma2-Maximum disturbance wave growth rate ki-max

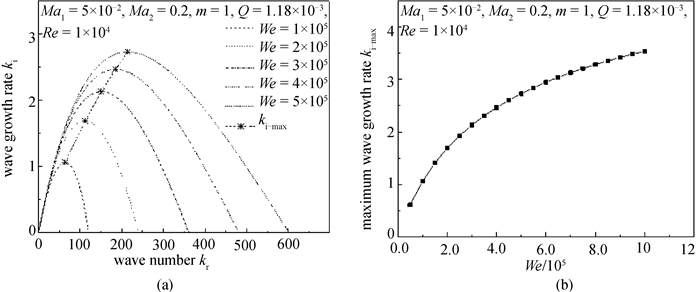
图4 韦伯数We对扰动波增长率的影响(a) 波数kr-扰动增长率ki；(b)韦伯数We-最大扰动增长率ki-max

Fig.4 Influence of Weber number We on the growth rate of disturbance wave (a) Wave number kr-Disturbance wave growth rate ki; (b) We-Maximum disturbance wave growth rate ki-max

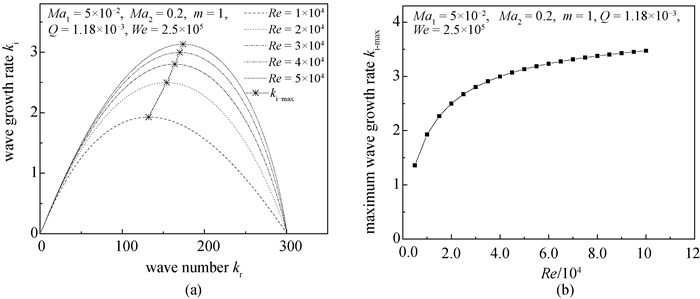
图5 雷诺数Re对扰动波增长率的影响(a) 波数kr -扰动增长率ki；(b) 雷诺数Re-最大扰动增长率ki-max

Fig.5 Influence of Reynolds number Re on the growth rate of disturbance wave (a) Wave number kr-Disturbance wave growth rate ki; (b) Re-Maximum disturbance wave growth rate ki-max

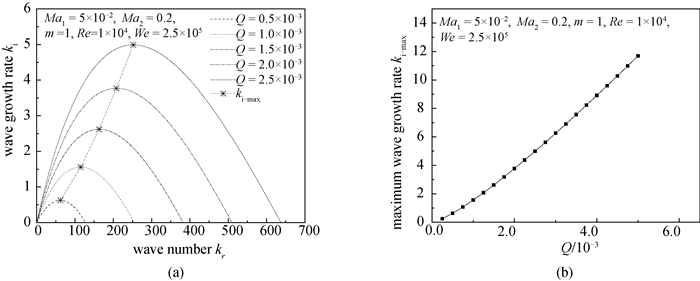
图6 气液密度比Q对扰动波增长率的影响(a) 波数kr-扰动增长率ki；(b) 气液密度比Q-最大扰动增长率ki-max

Fig.6 Influence of gas-liquid density ratio Q on the growth rate of disturbance wave (a) Wave number kr-Disturbance wave growth rate ki; (b) Q-Maximum disturbance wave growth rate ki-max

参考文献 35

1	李帅兵, 司廷. 射流破碎的线性不稳定性分析方法[J]. 空气动力学学报, 2019, 37 (03): 356- 372.
2	王晓英, 武识博, 王贞涛, 等. 液液系统中荷电射流不稳定性[J]. 排灌机械工程学报, 2020, 38 (06): 596- 601.
3	REITZ R D , BRACCO F V . Mechanism of atomization of a liquid jet[J]. Physics of Fluids, 1998, 25 (10): 1730- 1742.
4	LIN S P , KANG D J . Atomization of a liquid jet[J]. Physics of Fluids, 1987, 30 (7): 2000- 2000. DOI
5	LIN S P , LIAN Z W . Mechanisms of the breakup of liquid jets[J]. Aiaa Journal, 1990, 28 (1): 120- 126. DOI
6	YANG H Q . Asymmetric instability of a liquid jet[J]. Physics of Fluids A: Fluid Dynamics, 1992, 4 (4): 681- 689. DOI
7	LI X G . Mechanism of atomization of a liquid jet[J]. Atomization and Sprays, 1995, 66 (1): 113- 120.
8	CHEN T B , LI X G . Liquid jet atomization in a compressible gas stream[J]. Journal of Propulsion and Power, 1999, 15 (03): 369- 376. DOI
9	史绍熙, 郗大光, 秦建荣, 等. 高速粘性液体射流的不稳定模式[J]. 内燃机学报, 1997, 15 (01): 4- 10.
10	杜青, 刘宁, 杨延相, 等. 受激液体燃料射流表面波规律初探[J]. 内燃机学报, 2001, 19 (06): 511- 516. DOI
11	ZHOU Z W , LIN S P . Absolute and convective instability of a compressible jet[J]. Physics of Fluids A: Fluid Dynamics, 1992, 4 (2): 277- 282. DOI
12	严春吉. 可压缩气体中的三维黏性液体射流雾化机理[J]. 内燃机学报, 2007, 25 (04): 346- 351. DOI
13	严春吉, 解茂昭, 殷佩海. 粘性气体中粘性液体射流分裂与雾化机理研究[J]. 空气动力学学报, 2004, 22 (04): 422- 426. DOI
14	严春吉, 解茂昭. 液体射流分裂与雾化机理在喷雾特性预测中的应用[J]. 应用基础与工程科学学报, 2007, 15 (04): 552- 558. DOI
15	YANG L J , TONG M X , FU Q F . Linear stability analysis of a three-dimensional viscoelastic liquid jet surrounded by a swirling air stream[J]. Journal of Non-Newtonian Fluid Mechanics, 2013, 191 (191): 1- 13.
16	GUO L M , LV M , NING Z . Stability of a viscous liquid jet in a coaxial twisting compressible airflow[J]. Processes, 2021, 9 (6): 918- 918. DOI
17	吕明, 宁智, 阎凯, 等. 同轴旋转可压缩流动中液体射流稳定性[J]. 力学学报, 2013, 45 (03): 323- 330.
18	吕明, 宁智, 阎凯. 线性与非线性稳定性理论下液体射流空间发展的对比研究[J]. 物理学报, 2016, 65 (16): 192- 200.
19	吕明, 宁智, 阎凯. 同轴旋转可压缩气体中液体射流形态[J]. 内燃机学报, 2020, 38 (01): 81- 89.
20	邓甜, 李佳周, 陈伟. 剪切气流中无黏液体横向射流破碎机理[J]. 航空学报, 2021, 42 (07): 148- 158.
21	邓甜, 李佳周, 陈伟. 粘性液体横向射流破碎机理研究[J/OL]. 航空学报: 1-15(2021-06-07)[2022-02-23]. https://kns-cnki-net.webvpn.ncepu.edu.cn/kcms/detail/11.1929.v.20210604.1128.002.html.
22	吕明, 宁智, 阎凯. 可压缩旋转气体中超空化射流的热稳定性[J]. 力学学报, 2018, 50 (03): 561- 569.
23	阎凯, 宁智, 赵晋, 等. 存在温度扰动的圆环旋转黏性液体射流稳定性[J]. 高校化学工程学报, 2020, 34 (01): 86- 95.
24	张涛, 陈君, 李永平, 等. 具有线性温度分布的射流失稳研究[J]. 内燃机学报, 2020, 38 (03): 273- 279.
25	YI S J , XIE M Z , CHEN B X . The breakup and atomization of a viscous liquid jet[J]. Acta Mechanica Sinica, 1996, 12 (02): 124- 134.
26	WANG X P , LI X K . Log-conformation-based pressure-stabilized fractional step algorithm for viscoelastic flows[J]. Chinese Journal of Computational Physics, 2011, 28 (06): 853- 860.
27	MAO J , XIANG K , WANG Y L , et al. Numerical simulation of magnetohydrodynamic duct flow with sudden expansion[J]. Chinese Journal of Computational Physics, 2018, 35 (05): 597- 605.
28	MA Y W , FU D X . Numerical simulation of the near region of compressible axisymmetric jet[J]. Chinese Journal of Computational Physics, 2000, 17 (04): 341- 346.
29	JIANG Y , LI H , HUA L , ZHANG D M . Three-dimensional flow breakup characteristics of a 。ular jet with different nozzle geometries[J]. Biosystems Engineering, 2020, 193 (193): 216- 231.
30	SHANGGUAN Y Q , WANG X , LI Y M . High-performance numerical simulation of jet in cross-flow based on lattice Boltzmann method[J]. Chinese Journal of Computational Physics, 2015, 32 (06): 669- 676.
31	严春吉, 解茂昭. 液体射流扰动控制方程边界条件及稳定性分析[J]. 工程数学学报, 2008, 25 (03): 563- 566.
32	曹建明, 王德超, 舒力, 等. 射流动力学边界条件的研究[J]. 新能源进展, 2019, 7 (05): 436- 447.
33	曹建明, 彭畅. 射流碎裂过程的不稳定性理论研究[J]. 新能源进展, 2021, 9 (01): 55- 61.
34	MULLER , DAVID E . A method for solving algebraic equations using an automatic computer[J]. Mathematics of Computation, 1956, 10 (56): 208- 215.
35	杜青, 史绍熙, 刘宁, 等. 液体燃料射流最不稳定频率的理论分析(1)——液体燃料射流的最不稳定频率及无量纲数的影响[J]. 内燃机学报, 2000, 18 (03): 283- 287.

[1]	李子丰, 杨宁. 模拟射流雾化过程的VOF-LPT耦合方法[J]. 计算物理, 2022, 39(4): 440-452.
[2]	房尧立, 王一. 一种求解二维辐射流体力学方程组的显隐式格式[J]. 计算物理, 2021, 38(4): 401-417.
[3]	李康, 李守先, 刘娜. 强爆炸火球辐射流体自适应网格高精度数值模拟[J]. 计算物理, 2021, 38(2): 146-152.
[4]	陈锋, 许爱国, 张广财, 焦培刚. 一个三维多松弛时间全速域格子Boltzmann模型[J]. 计算物理, 2018, 35(4): 379-387.
[5]	郭少冬, 贾祖朋, 熊俊, 周海兵. 基于界面捕捉的三维多介质辐射流体力学方程MMALE计算方法[J]. 计算物理, 2018, 35(2): 127-137.
[6]	李凌霄. 不可压缩流基于块预处理的并行有限元计算[J]. 计算物理, 2018, 35(2): 151-160.
[7]	段茂昌, 蔚喜军, 陈大伟, 黄朝宝, 安娜. DG方法求解可压缩气固两相流动[J]. 计算物理, 2017, 34(6): 631-640.
[8]	李馨东, 赵英奎, 欧阳碧耀, 胡宗民, 姜宗林. 气体体积粘性对二维环形激波聚焦的影响[J]. 计算物理, 2017, 34(4): 394-402.
[9]	赵国忠, 蔚喜军, 郭怀民. 二维Lagrangian坐标系下可压气动方程组的间断Petrov-Galerkin方法[J]. 计算物理, 2017, 34(3): 294-308.
[10]	许亮, 冯成亮, 刘铁钢. 虚拟流体方法的设计原则[J]. 计算物理, 2016, 33(6): 671-680.
[11]	殷景岳, 罗喜胜. 管流中注入粒子的非定常波系的数值研究[J]. 计算物理, 2016, 33(4): 391-398.
[12]	刘中玉, 张明锋, 郑冠男, 杨国伟. 基于预处理HLLEW格式的全速域数值算法[J]. 计算物理, 2016, 33(3): 273-282.
[13]	上官燕琴, 王娴, 李跃明. 基于格子Boltzmann方法的平板射流大涡模拟[J]. 计算物理, 2015, 32(6): 669-676.
[14]	孙文俊, 范征峰. 辐射流体力学的分子动理学自适应加密方法(英文)[J]. 计算物理, 2015, 32(3): 277-292.
[15]	赵国忠, 蔚喜军, 李珍珍. 多介质流模拟的Runge-Kutta控制体积间断有限元方法[J]. 计算物理, 2014, 31(3): 271-284.