弱磁化等离子体中受激拉曼散射和受激布里渊散射抑制研究

doi:10.19596/j.cnki.1001-246x.8569

摘要/Abstract

摘要：

本文针对典型激光聚变等离子体参数条件, 利用动理学粒子模拟程序研究横向磁场和激光带宽在抑制受激拉曼散射(SRS)和受激布里渊散射(SBS)中的作用。模拟发现横向磁场对非均匀等离子体中SRS的非线性自共振增强有显著抑制作用, 分析认为横向磁场作用于SRS激发的电子等离子体波(EPW)势阱中的俘获电子, 使它们在横向上加速, 对EPW造成非线性阻尼, 同时减小EPW的非线性频移量, 从而缩窄非均匀等离子体中SRS的自共振空间, 极大降低SRS反射率。在此基础上利用横向磁场抑制SRS的特性, 以及SBS增长对激光带宽的敏感性, 提出了利用横向磁场和宽带激光将SRS和SBS同时抑制在低反射率水平的方案。在采用数十特斯拉横向磁场和实验中易于达到的千分之一量级的激光带宽时以及慢性约束聚变(ICF)相关参数下, SBS和SRS的反射率都得到了有效抑制。

关键词: 受激拉曼散射, 受激布里渊散射, 非线性动理学效应, 磁化等离子体, 自共振

Abstract:

Finding ways to suppress stimulated Raman scattering(SRS) and stimulated Brillouin scattering(SBS) is an important subject in inertial confinement fusion(ICF). Under the typical laser fusion plasma conditions, the effects of transverse magnetic field and laser bandwidth on the suppression of SRS and SBS are studied by utilizing the particle-in-cell(PIC) program. It is found that the transverse magnetic field can significantly inhibit the autoresonance of SRS in the non-uniform plasma. The transverse magnetic field accelerates the electrons trapped in the electron plasma wave(EPW) excited by SRS, which causes the nonlinear damping and reduces the nonlinear frequency shift of the EPW, thus narrowing the autoresonance space and significantly reducing the SRS reflectivity. Based on the characteristics that SRS can be suppressed by a transverse magnetic field and the SBS growth is sensitive to the laser bandwidth, a scheme is proposed that utilizing the transverse magnetic field and the broadband laser to suppress SRS and SBS simultaneously. When the transverse magnetic field is on the order of 10 T and the bandwidth is on the order of 0.001, both of which are easy to achieve in experiments, the total reflectivity of SRS and SBS can be effectively suppressed in the ICF-related plasmas.

Key words: stimulated Raman scattering, stimulated Brillouin scattering, nonlinear kinetic effect, magnetized plasma, autoresonance

周远志, 郑春阳, 刘占军, 曹莉华, 程瑞锦, 贺贤土. 弱磁化等离子体中受激拉曼散射和受激布里渊散射抑制研究[J]. 计算物理, 2023, 40(2): 136-146.

Yuanzhi ZHOU, Chunyang ZHENG, Zhanjun LIU, Lihua CAO, Ruijin CHENG, Xiantu HE. Suppression of Stimulated Raman Scattering and Stimulated Brillouin Scattering in Weakly Magnetized Plasmas[J]. Chinese Journal of Computational Physics, 2023, 40(2): 136-146.

图/表 9

图1 当入射激光I0 = 5 × 1015 W ·cm-2时，不同外加磁场下EPWs在时空中的演化

Fig.1 Snapshot of the spatial evolution of EPWs in different Bext when I0 = 5 × 1015 W ·cm-2

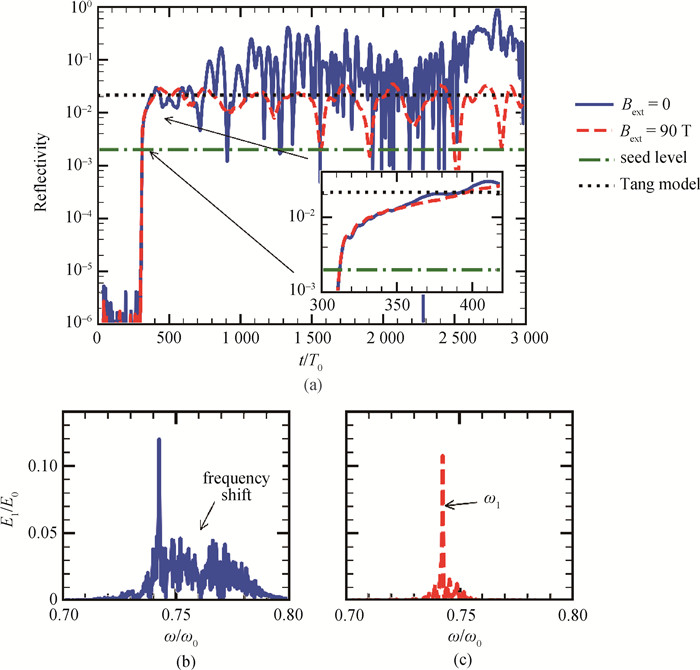
图2 (a) 在左边界测量得到的SRS反射率的包络线，模拟中的激光强度为I0=5×1015 W ·cm-2。绿色虚线和黑色点线分别代表了初始的种子光水平和理论预测的动理学增益后的反射水平。T0是泵浦光的周期。(b)和(c)在左边界测量得到的散射光的频率分布，测量的是磁场条件为Bext=0或Bext=90 T时的情况。

Fig.2 (a) Reflectivity of the scattered light at the left boundary when I0 = 5 × 1015 W ·cm-2. The green dash-dot line and black dotted line represent the initial seed level and the level expected by kinetic amplification respectively. T0 is the period of pump light. Frequency distributions of the scattered light waves at the left boundary when (b) Bext=0 or (c) Bext=90 T.

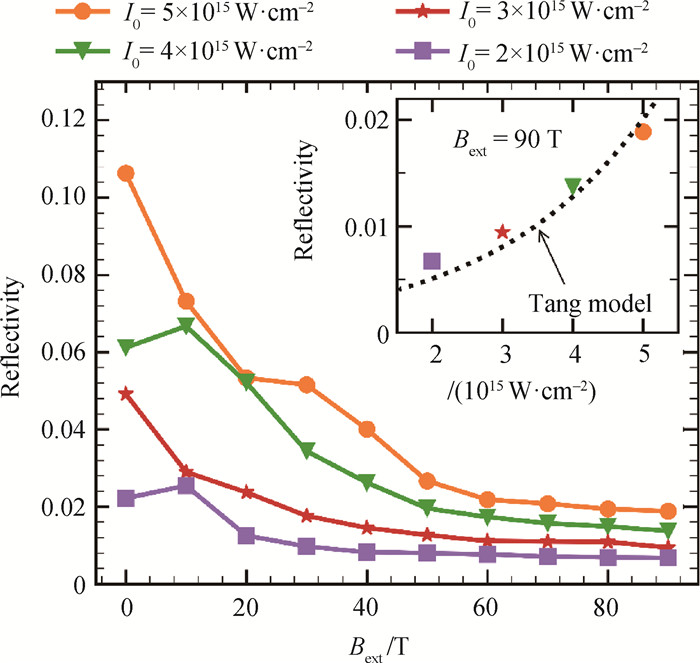
图3 不同外加磁场和不同入射光条件下时间平均的SRS反射率(种子光强度为泵浦光的1/500，模拟时间为3.5 ps。)

Fig.3 Time averaged SRS reflectivity under different magnetic fields and different pump lights (The seed light intensity is 1/500 of the pump light, and the simulation time is 3.5 ps.)

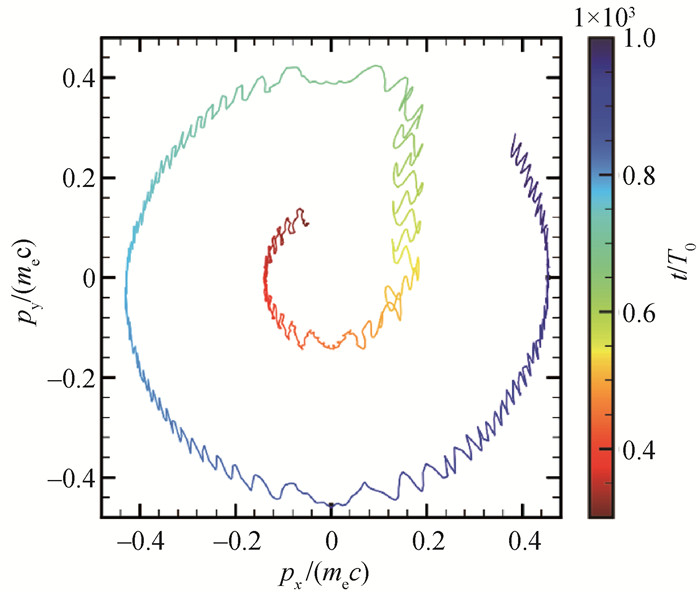
图4 在粒子模拟中追踪得到的电子运动轨迹(ωL/ωc=87.4，ωB/ωc=15.7, vpL/c=0.15。)

Fig.4 Orbit of an electron in the particle-in-cell (PIC) (ωL/ωc=87.4, ωB/ωc=15.7, vpL/c=0.15.)

图5 在t=600 T0时刻统计得到的电子在px-py空间上的分布函数

Fig.5 The electron distribution in px-py space at t=600 T0

表1 SBS和SRS的主要参数

Table 1 Main parameters of SBS and SRS

散射机制	kλ_De	ω/ω₀	γ₀/ω₀	ν_LD	G
SBS	0.367	0.997	5.63 × 10^-4	-0.104ω_a	3.65
SRS	0.313	0.276	2.25 × 10^-3	-0.0144ω_L	4.46

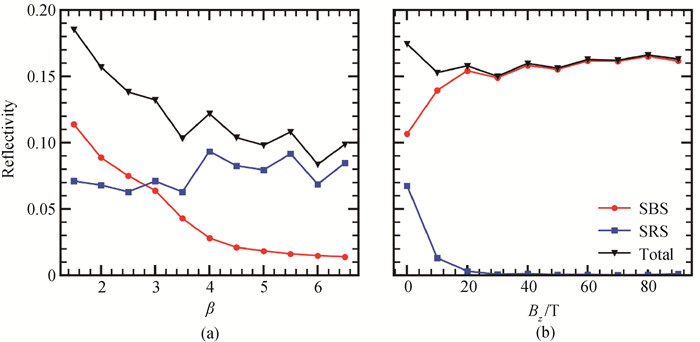
图6 (a) 无外加磁场时，反射率随入射激光带宽的变化; (b) 单色光入射时，反射率随横向磁场强度的变化

Fig.6 (a) The reflectivity changes with the bandwidth of the pump light when Bext= 0; (b) The reflectivity changes with the intensity of transverse magnetic field when the incident light is monochromatic

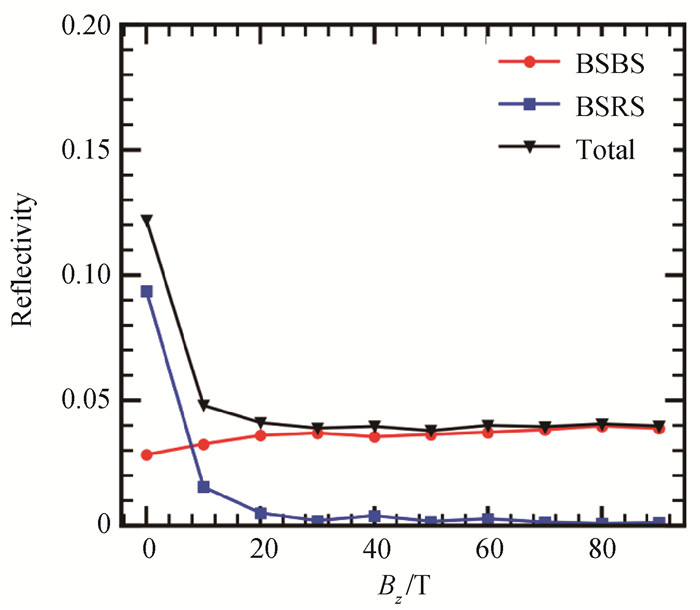
图7 固定带宽为2 × 10-3ω0时，SRS和SBS的反射率随横向磁场强度的变化

Fig.7 When the fixed bandwidth is 2 × 10-3ω0, the reflectivity of SRS and SBS changes with the intensity of transverse magnetic field

表2 不同方案下的激光透射率

Table 2 Transmittivity in different schemes

无抑制方案	2 × 10^-3带宽	20 T横向磁场	带宽+磁场
0.788	0.837	0.850	0.941

参考文献 46

1	HINKEL D E , ROSEN M D , WILLIAMS E A , et al. Stimulated Raman scatter analyses of experiments conducted at the National Ignition Facility[J]. Phys Plasmas, 2011, 18 (5): 056312. DOI
2	DEWALD E L , HARTEMANN F , MICHEL P , et al. Generation and beaming of early hot electrons onto the capsule in laser-driven ignition hohlraums[J]. Phys Rev Lett, 2016, 116 (7): 075003. DOI
3	YU Chengxin , FAN Zhengfeng , LIU Jie , et al. Modeling of shell-mixing into central hotspot in inertial confinement fusion implosion[J]. Chinese Journal of Computational Physics, 2017, 34 (4): 379- 386. DOI
4	YIN L , ALBRIGHT B J , BOWERS K J , et al. Saturation of backward stimulated scattering of laser in kinetic regime: Wavefront bowing, trapped particle modulational instability, and trapped particle self-focusing of plasma waves[J]. Phys Plasmas, 2008, 15 (1): 013109. DOI
5	O'NEIL T . Collisionless damping of nonlinear plasma oscillations[J]. Phys Fluids, 1965, 8 (12): 2255- 2262. DOI
6	VU H X V , DUBIOS D F , BEZZERIDES B . Inflation threshold: A nonlinear trapping-induced threshold for the rapid onset of stimulated Raman scattering from a single laser speckle[J]. Phys Plasmas, 2007, 14 (1): 012702. DOI
7	WANG Qing , LIU Zhanjun , ZHENG Chunyang , et al. Transition from convective to absolute Raman instability via the longitudinal relativistic effect by using Vlasov-Maxwell simulations[J]. Phys Plasmas, 2018, 25 (1): 012708. DOI
8	WANG Yanxia , WANG Qing , ZHENG Chunyang , et al. Nonlinear transition from convective to absolute Raman instability with trapped electrons and inflationary growth of reflectivity[J]. Phys Plasmas, 2018, 25 (10): 100702. DOI
9	MORALES G J , O'NEIL T M . Nonlinear frequency shift of an electron plasma wave[J]. Phys Rev Lett, 1972, 28 (7): 417- 420. DOI
10	LI Xin , WU Changshu , ZOU Shiyang , et al. 2D-simulation design of an ignition hohlraum[J]. Chinese Journal of Computational Physics, 2013, 30 (3): 371- 378.
11	LI Lingxiao , ZHAI Chuanlei , XIE Hui , et al. A monolithic preconditioned iterative solver and parallel computing for three-dimensional thermal radiation transport equation[J]. Chinese Journal of Computational Physics, 2021, 38 (3): 269- 279.
12	KLIMO O , WEBER S , TIKHONCHUK V T , et al. Particle-in-cell simulations of laser-plasma interaction for the shock ignition scenario[J]. Plasma Phys Control Fusion, 2010, 52 (5): 055013. DOI
13	ZHANG Hanchu , XIAO Chengzhuo , WANG Qing , et al. Effect of density modulation on backward stimulated Raman scattering in a laser-irradiated plasma[J]. Phys Plasmas, 2017, 24 (3): 032118. DOI
14	FERNANDEZ J C , COBBLE J A , FAILOR B H , et al. Observed dependence of stimulated Raman scattering on ion-acoustic damping in hohlraum plasmas[J]. Phys Rev Lett, 1996, 77 (13): 2702- 2705. DOI
15	KIRKWOOD R K , MACGOWAN B J , MONTGOMERY D S , et al. Effect of ion-wave damping on stimulated Raman scattering in high-Z laser-produced plasmas[J]. Phys Rev Lett, 1996, 77 (13): 2706- 2709. DOI
16	XU Feng , CAO Lihua . Theoretical and numerical studies on stimulated Raman scattering by a chirped laser pulse[J]. Chinese Journal of Computational Physics, 2011, 28 (4): 589- 597.
17	ZHAO Yao , YU Lule , ZHENG Jun , et al. Effects of large laser bandwidth on stimulated Raman scattering instability in underdense plasma[J]. Phys Plasmas, 2015, 22 (5): 052119. DOI
18	ZHAO Yao , WU C F , WENG Suming , et al. Mitigation of multibeam stimulated Raman scattering with polychromatic light[J]. Plasma Phys Control Fusion, 2021, 63 (5): 055006. DOI
19	DORRER C , HILL E M , ZUEGEL J D . High-energy parametric amplification of spectrally incoherent broadband pulses[J]. Opt Express, 2020, 28 (1): 451- 471. DOI
20	BATES J W , MYATT J F , SHAW J G , et al. Mitigation of cross-beam energy transfer in inertial confinement-fusion plasmas with enhanced laser bandwidth[J]. Phys Rev E, 2018, 97 (6): 06120.
21	DIVOL L . Controlling stimulated Brillouin backscatter with beam smoothing in weakly damped systems[J]. Phys Rev Lett, 2007, 99 (15): 155003. DOI
22	FROULA D H , DIVOL L , BERGER R L , et al. Direct measurements of an increased threshold for stimulated brillouin scattering with polarization smoothing in ignition hohlraum plasmas[J]. Phys Rev Lett, 2008, 101 (11): 115002. DOI
23	FUJIOKA S , ZHANG Z , ISHIHARA K , et al. Kilotesla magnetic field due to a capacitor-coil target driven by high power laser[J]. Sci Rep, 2013, 3, 1170. DOI
24	WAGNER U , TATARAKIS M , GOPAL A , et al. Laboratory measurements of 0.7 GG magnetic fields generated during high-intensity laser interactions with dense plasmas[J]. Phys Rev E, 2004, 70 (2): 026401. DOI
25	PERKINS L J , LOGAN B G , ZIMMERMAN G B , et al. Two-dimensional simulations of thermonuclear burn in ignition-scale inertial confinement fusion targets under compressed axial magnetic fields[J]. Phys Plasmas, 2013, 20 (7): 072708. DOI
26	JOGLEKAR A S , RIDGERS C P , KINGHAM R J , et al. Kinetic modeling of Nernst effect in magnetized hohlraums[J]. Phys Rev E, 2016, 93 (4): 043206. DOI
27	MONTGOMERY D S , ALBRIGHT B J , BARNAK D H , et al. Use of external magnetic fields in hohlraum plasmas to improve laser-coupling[J]. Phys Plasmas, 2015, 22 (1): 010703. DOI
28	LIU Z J , LI B , XIANG J , et al. Faraday effect on stimulated Raman scattering in the linear region[J]. Plasma Phys Control Fusion, 2018, 60 (4): 045008. DOI
29	YIN L , ALBRIGHT B J , ROSE H A , et al. Self-organized coherent bursts of stimulated Raman scattering and speckle interaction in multi-speckled laser beams[J]. Phys Plasmas, 2013, 20 (1): 012702. DOI
30	SAJAL V , DAHIYA D , TRIPATHI V K . Stimulated forward Raman scattering of a laser in a magnetized plasma[J]. Phys Plasmas, 2007, 14 (3): 032109. DOI
31	KATSOULEAS T , DAWSON J M . Unlimited electron acceleration in laser-driven plasma waves[J]. Phys Rev Lett, 1983, 51 (5): 392- 395. DOI
32	DAWSON J M , DECYK V K , HUFF R W , et al. Damping of large-amplitude plasma waves propagating perpendicular to the magnetic field[J]. Phys Rev Lett, 1983, 50 (19): 1455- 1458. DOI
33	DIECKMANN M E , SIRCOMBE N J , PARVIAINEN M , et al. Phase speed of electrostatic waves: The critical parameter for efficient electron surfing acceleration[J]. Plasma Phys Control Fusion, 2006, 48 (4): 489- 508. DOI
34	VIEIRA J , MARTINS J L , PATHAK V B , et al. Magnetically assisted self-injection and radiation generation for plasma-based acceleration[J]. Plasma Phys Control Fusion, 2012, 54 (12): 124044. DOI
35	KRASOVSKY V L . Damping of a plasma wave with trapped electrons in a weak transverse magnetic field[J]. Plasma Phys Rep, 2007, 33, 839- 849. DOI
36	WINJUM B J , TSUNG F S , MORI W B . Mitigation of stimulated Raman scattering in the kinetic regime by external magnetic fields[J]. Phys Rev E, 2018, 98 (4): 043208. DOI
37	YAAKOBI O , FRIEDLAND L , LINDBERG R R , et al. Spatially autoresonant stimulated Raman scattering in nonuniform plasmas[J]. Phys Plasmas, 2008, 15 (3): 032105. DOI
38	CHAPMAN T , MASSON-LABORDE P E , HULLER S , et al. Driven spatially autoresonant stimulated Raman scattering in the kinetic regime[J]. Phys Plasmas, 2010, 17 (12): 122317. DOI
39	DRAKE J F , KAW P K , LEE Y C , et al. Parametric instabilities of electromagnetic waves in plasmas[J]. Phys Fluids, 1974, 17 (4): 778- 785. DOI
40	WANG Qing , ZHENG Chunyang , LIU Zhanjun , et al. Auto-resonant stimulated Brillouin backscattering in supersonic flowing plasmas by fully kinetic Vlasov simulations[J]. Plasma Phys Control Fusion, 2019, 61 (8): 085017. DOI
41	TANG C L . Saturation and spectral characteristics of the stokes emission in the stimulated Brillouin process[J]. J Appl Phys, 1966, 37 (8): 2945- 2955. DOI
42	BERGER R L , BRUNNER S , CHAPMAN T , et al. Electron and ion kinetic effects on nonlinearly driven electron plasma and ion acoustic waves[J]. Phys Plasmas, 2013, 20 (3): 032107. DOI
43	DEWAR R L , KRUER W L , MANHEIMER W M . Modulational instabilities due to trapped electrons[J]. Phys Rev Lett, 1972, 28 (4): 215- 217. DOI
44	ARBER T D , BENNETT K , BRADY C S , et al. Contemporary particle-in-cell approach to laser-plasma modelling[J]. Plasma Phys Control. Fusion, 2015, 57 (11): 1- 26.
45	FARMER W A , KONING J M , STROZZI D J , et al. Simulation of self-generated magnetic fields in an inertial fusion hohlraum environment[J]. Phys Plasmas, 2017, 24 (5): 052703. DOI
46	KARNER C F F . Stochastic ion heating by a lower hybrid wave[J]. Phys Fluids, 1978, 21 (9): 1584- 1599. DOI

[1]	刘占军, 王强, 张文帅, 李斌, 李纪伟, 曹莉华, 郑春阳, 贺贤土. 三维大尺度激光等离子体相互作用程序LAP3D在集束实验中的应用[J]. 计算物理, 2023, 40(2): 169-180.
[2]	禹化龙, 王石语, 吴嘉宸. 大功率激光单模光纤远距离传输的注入光纤光功率限值分析[J]. 计算物理, 2022, 39(2): 173-178.
[3]	郑召文, 杨利霞. 截断磁等离子体三维M-NPML吸收边界条件[J]. 计算物理, 2013, 30(6): 895-901.
[4]	许峰, 曹莉华. 啁啾激光脉冲受激拉曼散射理论和粒子模拟[J]. 计算物理, 2011, 28(4): 589-597.
[5]	钟双英, 刘崧. 一种高效计算各向异性磁化等离子体的时域有限差分算法[J]. 计算物理, 2009, 26(3): 415-421.
[6]	黄守江, 李芳. 电磁波在磁化等离子体中传播的时域有限差分模拟[J]. 计算物理, 2005, 22(4): 319-324.