非均匀等离子体对强激光传播及电子束输运的影响

doi:10.19596/j.cnki.1001-246x.8622

摘要/Abstract

摘要：

本文介绍近期针对非均匀等离子体对强激光传播和电子束输运影响取得的研究进展, 首先研究弱无序分布等离子体对强激光传播的影响, 提出强激光在弱无序等离子体中存在非线性分支流传输机制, 并阐明光电离效应及相对论效应对分支流的重要影响。此外, 研究等离子体密度梯度对相对论电子束输运过程的影响, 发现相对论电子束输运所激发的静电波在空间固定点处的波数或相速度随时间变化, 并且不依赖于等离子体密度的上升或下降, 静电波的局域空间波数最终随时间逐渐增大, 这导致在非均匀等离子体中静电波通过朗道阻尼方式将能量耗散转移给背景电子, 表现为一种由背景等离子体密度梯度引起的束流能量耗散新机制。

关键词: 非均匀等离子体, 强激光, 相对论电子束, 分支流, 朗道阻尼

Abstract:

This work introduces our recent research works on the propagation of intense laser and transport of relativistic electron beam in inhomogeneous plasmas. First of all, we investigated the propagation of intense laser pulse in plasma with randomly uneven density distribution and found a new nonlinear branched flow regime of intense laser propagation in inhomogeneous plasma. In particular, we identify the important effects played by the laser photoionization and relativistic motion of electrons. In addition, we also investigated the plasma density gradient effect on evolution of electrostatic wave excited by ultra-relativistic electron beam in inhomogeneous plasma. It is found that the local region wavenumber and phase velocity of the excited wave varies with time because of the plasma inhomogeneity. Independent of the positive and negative density gradient, the wavenumber finally increases with time. As a result, Landau damping gradually becomes dominant in the whole region of inhomogeneous plasma, and leads to transfer of the wave energy to background plasma electrons, presenting a novel energy dissipation regime caused by the plasma density gradient.

Key words: inhomogeneous plasma, intense laser, relativistic electron beam, branched flow, Landau damping

黄太武, 蒋轲, 李然, 周沧涛. 非均匀等离子体对强激光传播及电子束输运的影响[J]. 计算物理, 2023, 40(2): 147-158.

Taiwu HUANG, Ke JIANG, Ran LI, Cangtao ZHOU. Propagation of Intense Laser and Transport of Relativistic Electron Beam in Inhomogeneous Plasmas[J]. Chinese Journal of Computational Physics, 2023, 40(2): 147-158.

图/表 6

图1 (a) 初始电子密度空间分布ne/nc；(b) 相应的等离子体折射率η空间分布

Fig.1 Initial distributions of (a) electron density ne/nc and (b) plasma refractive index η

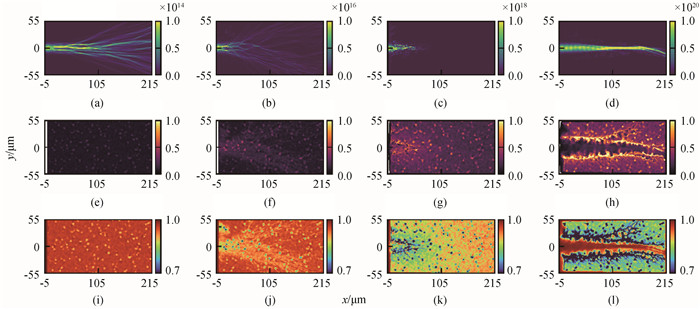
图2 (a)~(d) 激光强度空间分布I/(W·cm-2)；(c)~(h) 电子密度空间分布ne/nc；(i)~(l) 等离子体折射率η空间分布(从左至右I = 1014, 1016, 1018, 1020W·cm-2。)

Fig.2 Distributions of (a)~(d) laser intensity I/W·cm-2; (c)~(h) electron density ne/nc and (i)~(l) plasma refractive index η (From left to right, I = 1014, 1016, 1018, 1020 W·cm-2.)

图3 首个焦散面与源之间的距离d0与激光强度I的依赖关系

Fig.3 The distance from the source to the first caustics d0 for different laser intensities

图4 相对论电子束在等离子体(情形A和情形B)中输运时激发的静电波场(非均匀等离子体区域(区域Ⅱ)为100 μm~790 μm。)(a)~(b) t = 3 500 fs时刻(红线为情形B，蓝线为情形A)的静电波场; (c) 情形A中，x = 50 μm (品红线，位于区域Ⅰ)以及x = 900 μm(蓝线，位于区域Ⅲ)处电场随时间的变化; (d) 850 μm~950 μm非均匀区域内，情形B(红线)以及情形A(蓝线)的电场分布，所示时刻为t = 3 500 fs; (e) 情形A中，x = 270 μm(红线)、x = 445 μm(绿线)、以及x = 820 μm(蓝线)处电场随时间的变化

Fig.4 Electrostatic wave field excited by relativistic electron beam transport in background plasma in Cases A and B, where inhomogeneous plasma is distributed in the region of 100 μm~790 μm (a)~(b) electrostatic wave field for Case B (the red line) and Case A (the blue line) at t = 3 500 fs; (c) temporal evolution of the electric field at positions of x = 50 μm (the magenta line) and x = 900 μm (the blue line) in Case A; (d) electric field in the region of 850 μm~950 μm at t = 3 500 fs, where the red line represents the Case B and the blue one represents Case A; (e) temporal evolution of the electric field at positions of x = 270 μm (red line), x = 445 μm (green line), and x = 820 μm (blue line) in Case A

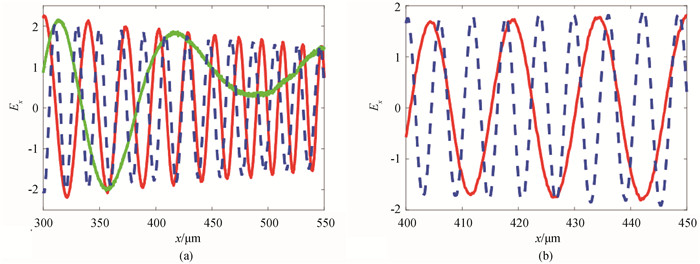
图5 (a) 情形B中300 ~ 550 μm区域内，t = 1 840 fs(红色实线)、t = 3 600 fs(绿色实线)以及t = 5 400 fs (蓝色虚线)时刻的静电波场分布; (b) 情形A中400 ~ 450 μm区域内，t = 1 840 fs(红色实线)以及t = 5 400 fs(蓝色虚线)时刻的静电波场分布

Fig.5 (a) Electrostatic wave field in the region of 300 ~ 550 μm for Case B at different time moments of t = 1 840 fs (red-solid line), t = 3 600 fs (green-solid line), and t = 5 400 fs (blue-dotted line); (b) electrostatic wave field in the region of 400 ~ 450 μm for Case A at different time moments of t = 1 840 fs (red-solid line) and t = 5 400 fs (blue-dotted line)

图6 (a) t ≈ 830 fs，情形C中50~250 μm区域内的静电波场分布; (b)~(d) 130~140 μm区域内，t ≈ 830 fs(红线)、t ≈ 2 800 fs(绿线)以及t ≈ 5 000 fs(蓝线)时刻的静电波场分布(在情形C中，非均匀等离子体分布在100~169 μm的区域。)

Fig.6 (a) Electrostatic wave field in 50~250 μm region for Case C at t ≈ 830 fs; (b)~(d) electrostatic wave field in 130~140 μm region at time moments of t ≈ 830 fs (red line), t ≈ 2 800 fs (green line), and t ≈ 5 000 fs (blue line) (In Case C, the inhomogeneous plasma is distributed in 100~169 μm.)

参考文献 61

1	DANSON C N , HAEFNER C , BROMAGE J , et al. Petawatt and exawatt class lasers worldwide[J]. High Power Laser Science and Engineering, 2019, 7 (e54): 03000e54.
2	YOON J H , KIM Y G , CHOI I W , et al. Realization of laser intensity over 10²³ W/cm²[J]. Optica, 2021, 8 (5): 630- 635. DOI
3	KASPARIAN J , RODRIGUEZ M , MEJEAN G , et al. White-light filaments for atmospheric analysis[J]. Science, 2003, 301 (5629): 61- 64. DOI
4	BETTI R , HURRICANE O A . Inertial-confinement fusion with lasers[J]. Nature Physics, 2016, 12, 435- 448. DOI
5	ESAREY E , SCHROEDER C B , LEEMANS W P . Physics of laser-driven plasma-based electron accelerators[J]. Review of Modern Physics, 2009, 81 (3): 1229- 1285. DOI
6	MACCHI A , BORGHESI M , PASSONI M . Ion acceleration by superintense laser-plasma interaction[J]. Review of Modern Physics, 2013, 85 (2): 751- 793. DOI
7	CORDES , PHUOC K TA , LAMBERT G , et al. Femtosecond x rays from laser-plasma accelerators[J]. Review of Modern Physics, 2013, 85 (1): 1- 48. DOI
8	REMINGTON B A , ARNETT D , DRAKE R P , et al. Modeling astrophysical phenomena in the laboratory with intense lasers[J]. Science, 1999, 284 (5419): 1488- 1493. DOI
9	PIAZZA A D , MULLER C , HATSAGORTSYAN K Z , et al. Extremely high-intensity laser interactions with fundamental quantum systems[J]. Review of Modern Physics, 2012, 84 (3): 1177- 1228. DOI
10	GONSALVES A J , NAKAMURA K , DANIELS J , et al. Petawatt laser guiding and electron beam acceleration to 8 GeV in a laser-heated capillary discharge waveguide[J]. Physical Review Letters, 2018, 122 (8): 084801.
11	HIGGINSON A , GARY R J , KING M , et al. Near -100 MeV protons via a laser-driven transparency-enhanced hybrid acceleration scheme[J]. Nature Communications, 2018, 9 (1): 724. DOI
12	CHEN H , HERMANN M R , KALANTAR D H , et al. High-energy (> 70 keV) x-ray conversion efficiency measurement on the ARC laser at the National Ignition Facility[J]. Physics of Plasmas, 2017, 24 (3): 033112. DOI
13	WANGW T , FENG K , KE L T , et al. Free-electron lasing at 27 nanometres based on a laser wakefield accelerator[J]. Nature, 2021, 595 (7868): 516- 520. DOI
14	ZYLSTRA A B , HURRICANE O A , CALLAHAN D A , et al. Burning plasma achieved in inertial fusion[J]. Nature, 2022, 601 (7894): 542- 548. DOI
15	贺贤土. 等离子体中大幅波与低频振荡粒子非线性相互作用效应[J]. 物理学报, 1982, 31 (10): 1317- 1336.
16	贺贤土. 等离子体波-粒子非线性作用的有质动力和自生磁场效应[J]. 物理学报, 1983, 32 (3): 325- 337.
17	ZHOUC T , HE X T , CHEN S G . Basic dynamic properties of the high-order nonlinear Schrödinger equation[J]. Physical Review A, 1992, 46 (5): 2277- 2285. DOI
18	ZHOUC T , HE X T , CAI T X . Pattern structures on generalized nonlinear schrodinger equations with various nonlinear terms[J]. Physical Review E, 1994, 50 (5): 4136- 4155. DOI
19	HEX T , ZHENG C Y . Spatiotemporal chaos in the regime of the conserved Zakharov equations[J]. Physical Review Letters, 1995, 74 (1): 78- 81. DOI
20	ZHUS P , HE X T , ZHENG C Y . Slow-time-scale magnetic fields driven by fast-time-scale waves in an underdense relativistic Vlasov plasma[J]. Physics of Plasmas, 2001, 8 (1): 321- 328. DOI
21	QIAO B , ZHU S P , ZHENG C Y , et al. Quasistatic magnetic and electric fields generated in intense laser plasma interaction[J]. Physics of Plasmas, 2005, 12 (5): 053104. DOI
22	LIU B , WANG H Y , LIU J , et al. Generating overcritical dense relativistic electron beams via self-matching resonance acceleration[J]. Physical Review Letters, 2013, 110 (4): 045002. DOI
23	HUANGT W , ROBINSON A P L , ZHOU C T , et al. Characteristics of betatron radiation from direct-laser-accelerated electrons[J]. Physical Review E, 2016, 93 (6): 063203. DOI
24	HEX T , LI J W , FAN Z F , et al. A hybrid-drive nonisobaric-ignition scheme for inertial confinement fusion[J]. Physics of Plasmas, 2016, 23 (8): 082706. DOI
25	ZHANG F , CAI H B , ZHOU W M , et al. Enhanced energy coupling for indirect-drive fast-ignition fusion targets[J]. Nature Physics, 2020, 16 (7): 810- 814. DOI
26	STROZZI D J , BAILEY D S , MICHEL P , et al. Interplay of laser-plasma interactions and inertial fusion hydrodynamics[J]. Physical Review Letters, 2017, 118 (2): 025002. DOI
27	HUSSEIN A E , AREFIEV A V , BATSON T , et al. Towards the optimisation of direct laser acceleration[J]. New Journal of Physics, 2021, 23, 023031. DOI
28	STARKD J , TONCIAN T , AREFIEV A V . Enhanced multi-MeV photon emission by a laser-driven electron beam in a self-generated magnetic field[J]. Physical Review Letters, 2016, 116 (18): 185003. DOI
29	HUANGT W , ZHOU C T , ZHANG H , et al. Collimated gamma photon emission driven by PW laser pulse in a plasma density channel[J]. Applied Physics Letters, 2017, 110 (2): 021002.
30	NORREYS P , BATANI D , BATON S , et al. Fast electron energy transport in solid density and compressed plasma[J]. Nuclear Fusion, 2014, 54 (5): 054004. DOI
31	SAKATA S , LEE S , MORITA H , et al. Magnetized fast isochoric laser heating for efficient creation of ultra-high-energy-density states[J]. Nature Communications, 2018, 9 (1): 3937. DOI
32	PUKHOV A , MEYER-TER-VEHN J . Relativistic magnetic self-channeling of light in near-critical plasma: Three-dimensional particle-in-cell simulation[J]. Physical Review Letters, 1996, 76 (21): 3975- 3978. DOI
33	HUANGT W , ZHOU C T , ROBINSON A P L , et al. Mitigating the relativistic laser beam filamentation via an elliptical beam profile[J]. Physical Review E, 2015, 92 (5): 053106. DOI
34	BIN J H , MA W J , WANG H Y , et al. Ion acceleration using relativistic pulse shaping in near-critical-density plasmas[J]. Physical Review Letters, 2015, 115 (6): 064801. DOI
35	LI G , MORI W B , REN C . Laser hosing in relativistically hot plasmas[J]. Physical Review Letters, 2013, 110 (15): 155002. DOI
36	HUANG T W , ZHOU C T , ZHANG H , et al. Relativistic laser hosing instability suppression and electron acceleration in a preformed plasma channel[J]. Physical Review E, 2017, 95 (4): 043207. DOI
37	RAWAT P , GAUNIYAL R , PUROHIT G . Growth of ring ripple in a collisionless plasma in relativistic-ponderomotive regime and its effect on stimulated Raman backscattering process[J]. Physics of Plasmas, 2014, 21 (6): 062109. DOI
38	DAVIES J R . Electric and magnetic field generation and target heating by laser-generated fast electrons[J]. Physical Review E, 2003, 68 (5): 056404. DOI
39	ZHOU C T , HE X T , YU M Y . Laser-produced energetic electron transport in overdense plasmas by wire guiding[J]. Applied Physics Letters, 2008, 92 (15): 151502. DOI
40	ZHOU C T , HE X T , CHEW L Y . Intense short-pulse lasers irradiating wire and hollow plasma fibers[J]. Optics Letters, 2011, 36 (6): 924- 926. DOI
41	BRET A , GREMILLET L , DIECKMANN M E . Multidimensional electron beam-plasma instabilities in the relativistic regime[J]. Physics of Plasmas, 2010, 17 (12): 120501. DOI
42	ROBINSON A P L , STROZZI D J , DAVIES J R , et al. Theory of fast electron transport for fast ignition[J]. Nuclear Fusion, 2014, 54 (5): 054003. DOI
43	蔡洪波, 周沧涛, 贾青, 等. 激光驱动强流电子束产生和控制[J]. 强激光与粒子束, 2015, 27 (3): 032001. DOI
44	YANG X H , ZHUO H B , XU H , et al. Effects of filamentation instability on the divergence of relativistic electrons driven by ultraintense laser pulses[J]. Physics of Plasmas, 2016, 23 (10): 103110. DOI
45	MATSUO K , HIGASHI N , IWATA N , et al. Petapascal pressure driven by fast isochoric heating with a multipicosecond intense laser pulse[J]. Physical Review Letters, 2020, 124 (3): 035001. DOI
46	LI R , HUANG T W , JU L B , et al. Nanoscale electrostatic modulation of mega-Ampere electron current in solid density plasmas[J]. Physical Review Letters, 2021, 127 (24): 245002. DOI
47	POMPILI R , ALESINI D , ANANIA M P , et al. Energy spread minimization in a beam-driven plasma wakefield accelerator[J]. Nature Physics, 2021, 17 (4): 499- 503. DOI
48	ZHANG H S , BETTI R , YAN R , et al. Self-similar multimode bubble-front evolution of the ablative Rayleigh Taylor instability in two and three dimensions[J]. Physical Review Letters, 2018, 121 (18): 185002. DOI
49	WAGNER F , BEDACHT S , ORTNER A , et al. Pre-plasma formation in experiments using petawatt lasers[J]. Optics Express, 2014, 22 (24): 29505. DOI
50	ZHANG C J , HUA J F , WAN Y , et al. Femtosecond probing of plasma wakefields and observation of the plasma wake reversal using a relativistic electron bunch[J]. Physical Review Letters, 2017, 119 (6): 064801. DOI
51	NAGAI K , MUSGRAVE C S A , NAZAROV W . A review of low density porous materials used in laser plasma experiments[J]. Physics of Plasmas, 2018, 25 (3): 030501. DOI
52	CIPRIANI M , GUSKOV S Y , CONSOLI F , et al. Time-dependent measurement of high-power laser light reflection by low-Z foam plasma[J]. High Power Laser Science and Engineering, 2021, 9 (e40): 03000e40.
53	HELLER E J , FLEISCHMANN R , KRAMER T . Branched flow[J]. Physics Today, 2021, 74 (12): 44- 51. DOI
54	SHANDARIN S F , ZELDOVICH Y B . The large-scale structure of the universe: Turbulence, intermittency, structures in a self-gravitating medium[J]. Review of Modern Physics, 1989, 61 (2): 185- 220. DOI
55	PIDWERBETSKY A. Simulation and analysis of wave propagation through random media[D]. New York: Cornell University, 1988.
56	TOPINKA M A , LEROY B J , WESTERVELT R M , et al. Coherent branched flow in a two-dimensional electron gas[J]. Nature, 2001, 410 (6825): 183- 186. DOI
57	DEGUELDRE H , METZGER J J , GEISEL T , et al. Random focusing of tsunami waves[J]. Nature Physics, 2016, 12 (3): 259- 262. DOI
58	PATSYK A , SIVAN U , SEGEV M , et al. Observation of branched flow of light[J]. Nature, 2020, 583 (7814): 60- 65. DOI
59	ARBER T D , BENNETT K , BRADY C S , et al. Contemporary particle-in-cell approach to laser plasma modelling[J]. Plasma Physics and Controlled Fusion, 2015, 57 (11): 113001. DOI
60	KAPLAN L . Statistics of branched flow in a weak correlated random potential[J]. Physical Review Letters, 2002, 89 (18): 184103. DOI
61	METZGER J J , FLEISCHMANN R , GEISEL T . Universal statistics of branched flows[J]. Physical Review Letters, 2010, 105 (2): 020601. DOI

[1]	吕文娟, 吴斌兵, 刘士炜, 段皓, 刘杰. 超强激光场中氘氚核聚变截面研究进展[J]. 计算物理, 2022, 39(2): 127-142.
[2]	常恒心, 许铮, 姚伟鹏, 谢雨, 乔宾. 量子电动力学—粒子模拟极端等离子体动力学研究[J]. 计算物理, 2017, 34(5): 526-542.
[3]	陈民, 盛政明, 郑君, 马燕云, 张杰. 粒子模拟程序的发展及其在激光等离子体相互作用研究中的应用[J]. 计算物理, 2008, 25(1): 43-50.
[4]	胡友俊, 杨维纮, 陈银华, 张羽. 磁化非均匀等离子体中模转换机制对电磁波吸收的数值研究[J]. 计算物理, 2007, 24(3): 330-336.
[5]	张公让, 匡光力. HT-7托卡马克中低杂波和离子波恩斯坦波协同作用的数值研究[J]. 计算物理, 2006, 23(3): 325-334.
[6]	刘世兴, 王怀民, 祁月盈, 刘学深, 丁培柱. 强激光场中CO分子经典轨迹的辛算法[J]. 计算物理, 2005, 22(4): 325-328.
[7]	祁月盈, 刘晓艳, 丁培柱. 强激光场中一维原子的渐近边界条件[J]. 计算物理, 2003, 20(5): 377-380.
[8]	刘学深, 刘晓艳, 杨玉军, 丁培柱, 朱颀人. 强场一维模型问题的保Wronskian守恒算法[J]. 计算物理, 2001, 18(6): 487-490.
[9]	蔡宗良, 张建泉, 刘峰, 强希文. 脉冲强激光产生的激波在靶材中的传播过程[J]. 计算物理, 1997, 14(S1): 426-428.
[10]	陈荣华, 张建泉, 李邦固, 刘峰, 强希文. 脉冲强激光冲击力学效应的数值模拟[J]. 计算物理, 1997, 14(S1): 682-683.
[11]	王敏, 李京. 虚阴极产生微波的一些基本特性[J]. 计算物理, 1996, 13(1): 38-42.
[12]	陈发良. 强激光照射下受预内压作用的球壳的热力响应[J]. 计算物理, 1994, 11(3): 269-277.
[13]	简广德, 潘传红. 在碰撞等离子体中阿尔芬(ALFVEN)波动力理论计算[J]. 计算物理, 1990, 7(4): 481-487.