计算物理 ›› 2024, Vol. 41 ›› Issue (1): 131-150.DOI: 10.19596/j.cnki.1001-246x.8778
• 面向超级计算机的性能优化技术与数值并行算法专刊 • 上一篇
许康1( ), 李泽阳1, 郭竹丰1, 沈颖童1, 王威1, 缑敏辉1, 王子正1, 王玉坤1,2,*(
), 李泽阳1, 郭竹丰1, 沈颖童1, 王威1, 缑敏辉1, 王子正1, 王玉坤1,2,*( ), 刘伟峰3,*(
), 刘伟峰3,*( )
)
收稿日期:2023-06-12
出版日期:2024-01-25
发布日期:2024-02-05
通讯作者:
王玉坤,刘伟峰
作者简介:许康(2000-), 男, 硕士研究生, E-mail: 623509112@qq.com
基金资助:
Kang XU1( ), Zeyang LI1, Zhufeng GUO1, Yingtong SHEN1, Wei WANG1, Minhui GOU1, Zizheng WANG1, Yukun WANG1,2,*(
), Zeyang LI1, Zhufeng GUO1, Yingtong SHEN1, Wei WANG1, Minhui GOU1, Zizheng WANG1, Yukun WANG1,2,*( ), Weifeng LIU3,*(
), Weifeng LIU3,*( )
)
Received:2023-06-12
Online:2024-01-25
Published:2024-02-05
Contact:
Yukun WANG, Weifeng LIU
摘要:
量子计算作为一种基于量子力学原理的全新计算模型, 具有强大的并行性和潜在的颠覆性影响力, 为解决复杂问题提供了新的思路。本文的主要目标是对量子计算在大规模科学与工程计算领域中数值计算问题的解法器算法和应用进行综述。重点介绍量子计算在线性方程组、特征值问题、微分方程、哈密顿量与图计算、量子机器学习、量子解法器平台以及实际数值模拟等领域的具体应用。针对不同的数值计算问题, 详细讨论当前主流的量子计算算法, 并总结近年来国内外相关算法的研究进展。最后, 对量子计算在数值计算求解相关研究方向的未来发展趋势进行展望。
中图分类号:
许康, 李泽阳, 郭竹丰, 沈颖童, 王威, 缑敏辉, 王子正, 王玉坤, 刘伟峰. 量子计算加速的解法器算法及应用综述[J]. 计算物理, 2024, 41(1): 131-150.
Kang XU, Zeyang LI, Zhufeng GUO, Yingtong SHEN, Wei WANG, Minhui GOU, Zizheng WANG, Yukun WANG, Weifeng LIU. A Review of Algorithms and Applications of Solvers with Quantum Computing Acceleration[J]. Chinese Journal of Computational Physics, 2024, 41(1): 131-150.
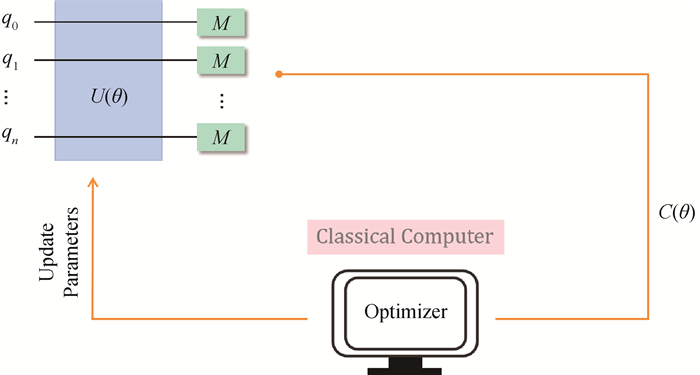
图2 变分量子算法示意图(使用经典优化器训练参数化量子电路,其中量子计算机采用含参数的酉门来处理整个算法计算复杂度高的部分,经典计算机负责处理参数的迭代更新(比如梯度下降算法)部分。)
Fig.2 Schematic diagram of the Variational Quantum Algorithm (The classical optimizer is used to train theparameterized quantum circuits, in which quantum computer uses the parameterized unitary gates to process thecomputationally difficult subroutines of the whole algorithm and the classical computer is responsible for theiterative updating of parameters, such as gradient descent algorithm.)
| 量子云平台 | 语言 | 性能 |
| 百度量易伏 | Python, C++ | 8个量子比特T1①: 31.0 μs T2②: 8.7 μs保真度③:99.80% |
| 华为HiQ | Python | 11个量子比特 |
| 本源 | Python, C++ | 12个量子比特T1: 20.82 μs T2: 4.14 μs保真度:99.78% |
| IBM | Python | 433个量子比特T1: 91.12 μs T2: 59.94 μs保真度:99.47% |
表1 部分量子云平台使用的语言和性能参数
Table 1 The language and performance parameters used by some quantum cloud platforms
| 量子云平台 | 语言 | 性能 |
| 百度量易伏 | Python, C++ | 8个量子比特T1①: 31.0 μs T2②: 8.7 μs保真度③:99.80% |
| 华为HiQ | Python | 11个量子比特 |
| 本源 | Python, C++ | 12个量子比特T1: 20.82 μs T2: 4.14 μs保真度:99.78% |
| IBM | Python | 433个量子比特T1: 91.12 μs T2: 59.94 μs保真度:99.47% |
| 1 | FEYNMAN R P .Simulating physics with computers[J].International Journal of Theoretical Physics,1982,21(6):467-488. |
| 2 | DEUTSCH D .Quantum theory, the Church-Turing principle and the universal quantum computer[J].Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,1985,400(1818):97-117. |
| 3 |
BERNSTEIN E , VAZIRANI U .Quantum complexity theory[J].SIAM Journal on Computing,1997,26(5):1411-1473.
DOI |
| 4 | CHI-CHIH YAO A. Quantum circuit complexity[C]//Proceedings of 1993 IEEE 34th Annual Foundations of Computer Science. Palo Alto, CA, USA: IEEE, 1993: 352-361. |
| 5 | DEUTSCH D , JOZSA R .Rapid solution of problems by quantum computation[J].Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,1992,439(1907):553-558. |
| 6 |
SIMON D R .On the power of quantum computation[J].SIAM Journal on Computing,1997,26(5):1474-1483.
DOI |
| 7 | SHOR P W. Algorithms for quantum computation: discrete logarithms and factoring[C]//Proceedings 35th Annual Symposium on Foundations of Computer Science. Santa Fe, NM, USA: IEEE, 1994: 124-134. |
| 8 | GROVER L K. A fast quantum mechanical algorithm for database search[C]//Proceedings of the twenty-eighth annual ACM symposium on Theory of Computing. Philadelphia, Pennsylvania, USA: Association for Computing Machinery, 1996: 212-219. |
| 9 | FARHI E, GOLDSTONE J, GUTMANN S. A quantum approximate optimization algorithm[EB/OL]. (2014-11-14)[2023-05-10]. https://doi.org/10.48550/arXiv.1411.4028. |
| 10 |
HARROW A W , HASSIDIM A , LLOYD S .Quantum algorithm for linear systems of equations[J].Physical Review Letters,2009,103(15):150502.
DOI |
| 11 |
REBENTROST P , SCHULD M , WOSSNIG L , et al.Quantum gradient descent and Newton's method for constrained polynomial optimization[J].New Journal of Physics,2019,21(7):073023.
DOI |
| 12 |
KERENIDIS I , PRAKASH A .Quantum gradient descent for linear systems and least squares[J].Physical Review A,2020,101(2):022316.
DOI |
| 13 |
SHAO Changpeng , XIANG Hua .Row and column iteration methods to solve linear systems on a quantum computer[J].Physical Review A,2020,101(2):022322.
DOI |
| 14 | AMBAINIS A. Variable time amplitude amplification and quantum algorithms for linear algebra problems[C]//29th International Symposium on Theoretical Aspects of Computer Science (STACS 2012). Paris, France: Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, 2012: 636-647. |
| 15 |
CHILDS A M , KOTHARI R , SOMMA R D .Quantum algorithm for systems of linear equations with exponentially improved dependence on precision[J].SIAM Journal on Computing,2017,46(6):1920-1950.
DOI |
| 16 | GILYÉN A, SU Yuan, LOW G H, et al. Quantum singular value transformation and beyond: Exponential improvements for quantum matrix arithmetics[C]//Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing. Phoenix, AZ, USA: Association for Computing Machinery, 2019: 193-204. |
| 17 |
WOSSNIG L , ZHAO Zhikuan , PRAKASH A .Quantum linear system algorithm for dense matrices[J].Physical Review Letters,2018,120(5):050502.
DOI |
| 18 | WANG Chunhao , WOSSNIG L .A quantum algorithm for simulating non-sparse Hamiltonians[J].Quantum Information and Computation,2020,20(7/8):597-615. |
| 19 |
CLADER B D , JACOBS B C , SPROUSE C R .Preconditioned quantum linear system algorithm[J].Physical Review Letters,2013,110(25):250504.
DOI |
| 20 |
SHAO Changpeng , XIANG Hua .Quantum circulant preconditioner for a linear system of equations[J].Physical Review A,2018,98(6):062321.
DOI |
| 21 |
PERUZZO A , MCCLEAN J , SHADBOLT P , et al.A variational eigenvalue solver on a photonic quantum processor[J].Nature Communications,2014,5,4213.
DOI |
| 22 |
XU Xiaosi , SUN Jinzhao , ENDO S , et al.Variational algorithms for linear algebra[J].Science Bulletin,2021,66(21):2181-2188.
DOI |
| 23 | BRAVO-PRIETO C, LAROSE R, CEREZO M, et al. Variational quantum linear solver[EB/OL]. (2020-06-02)[2023-05-10]. https://doi.org/10.48550/arXiv.1909.05820. |
| 24 | AN Dong , LIN Lin .Quantum linear system solver based on time-optimal adiabatic quantum computing and quantum approximate optimization algorithm[J].ACM Transactions on Quantum Computing,2022,3(2):1-28. |
| 25 |
HUANG H Y , BHARTI K , REBENTROST P .Near-term quantum algorithms for linear systems of equations with regression loss functions[J].New Journal of Physics,2021,23(11):113021.
DOI |
| 26 |
ZHENG Yarui , SONG Chao , CHEN Mingcheng , et al.Solving systems of linear equations with a superconducting quantum processor[J].Physical Review Letters,2017,118(21):210504.
DOI |
| 27 |
PAN Jian , CAO Yudong , YAO Xiwei , et al.Experimental realization of quantum algorithm for solving linear systems of equations[J].Physical Review A,2014,89(2):022313.
DOI |
| 28 |
BARZ S , KASSAL I , RINGBAUER M , et al.A two-qubit photonic quantum processor and its application to solving systems of linear equations[J].Scientific Reports,2014,4(1):6115.
DOI |
| 29 |
WEN Jingwei , KONG Xiangyu , WEI Shijie , et al.Experimental realization of quantum algorithms for a linear system inspired by adiabatic quantum computing[J].Physical Review A,2019,99(1):012320.
DOI |
| 30 | QIAN Peng, HUANG Weicong, LONG Guilu. A quantum algorithm for solving systems of nonlinear algebraic equations[EB/OL]. (2019-03-14)[2023-05-12]. https://doi.org/10.48550/arXiv.1903.05608. |
| 31 |
RIZK-ALLAH R M .A quantum-based sine cosine algorithm for solving general systems of nonlinear equations[J].Artificial Intelligence Review,2021,54(5):3939-3990.
DOI |
| 32 |
XUE Cheng , WU Yuchun , GUO Guoping .Quantum newton's method for solving the system of nonlinear equations[J].SPIN,2021,11(3):2140004.
DOI |
| 33 |
JIN Lei , SHAN Zheng , HU Chunchao , et al.Higher-order quantum genetic algorithm and its application on non-linear equations[J].Journal of Physics: Conference Series,2021,1827(1):012159.
DOI |
| 34 |
XUE Cheng , XU Xiaofan , WU Yuchun , et al.Quantum algorithm for solving a quadratic nonlinear system of equations[J].Physical Review A,2022,106(3):032427.
DOI |
| 35 |
BERRY D W .High-order quantum algorithm for solving linear differential equations[J].Journal of Physics A: Mathematical and Theoretical,2014,47(10):105301.
DOI |
| 36 |
BIAMONTE J , WITTEK P , PANCOTTI N , et al.Quantum machine learning[J].Nature,2017,549(7671):195-202.
DOI |
| 37 |
HESTENES M R , STIEFEL E .Methods of conjugate gradients for solving linear systems[J].Journal of Research of the National Bureau of Standards,1952,49(6):409-436.
DOI |
| 38 |
CEREZO M , ARRASMITH A , BABBUSH R , et al.Variational quantum algorithms[J].Nature Reviews Physics,2021,3(9):625-644.
DOI |
| 39 | 朱凯博, 徐龙飞, 潘流俊, 等.JFNK方法在S N输运计算中的应用[J].计算物理,2021,38(4):381-392. |
| 40 |
李帅龙, 崔国民, 陈家星, 等.一种采用种群多样性监控和实时更新策略的粒子群优化算法[J].计算物理,2017,34(3):344-354.
DOI |
| 41 |
FRANCIS J G F .The QR transformation-part 2[J].The Computer Journal,1962,4(4):332-345.
DOI |
| 42 |
KUBLANOVSKAYA V N .On some algorithms for the solution of the complete eigenvalue problem[J].USSR Computational Mathematics and Mathematical Physics,1962,1(3):637-657.
DOI |
| 43 | JACOBI C G J .Vber ein leichtes Verfahren die in der Theorie der Säcularstörungen vorkommenden Gleichungen numerisch aufzulösen[J].Journal für Die Reine und Angewandte Mathematik,2009,1846(30):51-94. |
| 44 | GOLUB G H , VAN DER VORST H A .Eigenvalue computation in the 20th century[J].Journal of Computational and Applied Mathematics,2000,123(1/2):35-65. |
| 45 |
ABRAMS D S , LLOYD S .Quantum algorithm providing exponential speed increase for finding eigenvalues and eigenvectors[J].Physical Review Letters,1999,83(24):5162-5165.
DOI |
| 46 |
WANG Daochen , HIGGOTT O , BRIERLEY S .Accelerated variational quantum eigensolver[J].Physical Review Letters,2019,122(14):140504.
DOI |
| 47 | D'CUNHA R, OTTEN M, HERMES M R, et al. State preparation in quantum algorithms for fragment-based quantum chemistry[EB/OL]. (2023-06-07)[2023-05-11]. https://doi.org/10.48550/arXiv.2305.18110. |
| 48 |
DOBŠÍČGEK M , JOHANSSON G , SHUMEIKO V , et al.Arbitrary accuracy iterative quantum phase estimation algorithm using a single ancillary qubit: A two-qubit benchmark[J].Physical Review A,2007,76(3):030306.
DOI |
| 49 |
WANG Hefeng , WU Lianao , LIU Yuxi , et al.Measurement-based quantum phase estimation algorithm for finding eigenvalues of non-unitary matrices[J].Physical Review A,2010,82(6):062303.
DOI |
| 50 | 吴绍君. 量子强化学习算法及其在特征值问题上的应用[D]. 成都: 电子科技大学, 2021. |
| 51 | 赵乾坤.量子迭代相位估计算法在IBM超导平台的实现[J].福建电脑,2023,39(2):6-10. |
| 52 |
RYABINKIN I G , GENIN S N , IZMAYLOV A F .Constrained variational quantum eigensolver: Quantum computer search engine in the Fock space[J].Journal of Chemical Theory and Computation,2019,15(1):249-255.
DOI |
| 53 |
LIANG Jinmin , SHEN Shuqian , LI Ming , et al.Variational quantum algorithms for dimensionality reduction and classification[J].Physical Review A,2020,101(3):032323.
DOI |
| 54 | WEI Shijie , LI Hang , LONG Guilu .A full quantum eigensolver for quantum chemistry simulations[J].Research,2020,2020,1486935. |
| 55 |
ZHANG Danbo , CHEN Binlin , YUAN Zhanhao , et al.Variational quantum eigensolvers by variance minimization[J].Chinese Physics B,2022,31(12):120301.
DOI |
| 56 | 张欣, 赵国忠, 李宏.局部间断Petrov-Galerkin方法在大气污染模型中的应用[J].计算物理,2021,38(2):171-182. |
| 57 |
KIANI B T , DE PALMA G , ENGLUND D , et al.Quantum advantage for differential equation analysis[J].Physical Review A,2022,105(2):022415.
DOI |
| 58 | KIM S , KARRILA S J .Microhydrodynamics: Principles and selected applications[M].Boston: Butterworth-Heinemann,2013. |
| 59 |
BERRY D W , CHILDS A M , OSTRANDER A , et al.Quantum algorithm for linear differential equations with exponentially improved dependence on precision[J].Communications in Mathematical Physics,2017,356(3):1057-1081.
DOI |
| 60 | SOMMA R .Quantum linear systems algorithm with exponentially improved dependence on precision[J].SIAM Journal on Computing,2015,46(6):1920-1950. |
| 61 | LEYTON S K, OSBORNE T J. A quantum algorithm to solve nonlinear differential equations[EB/OL]. (2008-12-23)[2023-05-11]. https://doi.org/10.48550/arXiv.0812.4423. |
| 62 | LIU Jinpeng , KOLDEN H Ø , KROVI H K , et al.Efficient quantum algorithm for dissipative nonlinear differential equations[J].Proceedings of the National Academy of Sciences of the United States of America,2021,118(35):e2026805118. |
| 63 | CARLEMAN T .Application de la théorie des équations intégrales linéaires aux systèmes d'équations différentielles non linéaires[J].Acta Mathematica,1932,59(1):63-87. |
| 64 |
CHEN Guoting , DELLA DORA J .An algorithm for computing a new normal form for dynamical systems[J].Journal of Symbolic Computation,2000,29(3):393-418.
DOI |
| 65 | LLOYD S, DE PALMA G, GOKLER C, et al. Quantum algorithm for nonlinear differential equations[EB/OL]. (2020-12-21)[2023-05-11]. https://doi.org/10.48550/arXiv.2011.06571. |
| 66 | BENEDIKTER N , PORTA M , SCHLEIN B .Effective evolution equations from quantum dynamics[M].Cham: Springer,2016. |
| 67 |
TROTTER H F .On the product of semi-groups of operators[J].Proceedings of the American Mathematical Society,1959,10(4):545-551.
DOI |
| 68 |
COSTA P C S , JORDAN S , OSTRANDER A .Quantum algorithm for simulating the wave equation[J].Physical Review A,2019,99(1):012323.
DOI |
| 69 |
LUBASCH M , JOO J , MOINIER P , et al.Variational quantum algorithms for nonlinear problems[J].Physical Review A,2020,101(1):010301.
DOI |
| 70 |
KYRⅡENKO O , PAINE A E , ELFVING V E .Solving nonlinear differential equations with differentiable quantum circuits[J].Physical Review A,2021,103(5):052416.
DOI |
| 71 |
MARTOŇÁK R , SANTORO G E , TOSATTI E .Quantum annealing of the traveling-salesman problem[J].Physical Review E,2004,70(5):057701.
DOI |
| 72 | PELOFSKE E, HAHN G, DJIDJEV H. Solving large maximum clique problems on a quantum annealer[C]//QTOP 2019: Quantum Technology and Optimization Problems. Munich, Germany: Springer, 2019: 123-135. |
| 73 |
CALUDE C S , DINNEEN M J , HUA R .QUBO formulations for the graph isomorphism problem and related problems[J].Theoretical Computer Science,2017,701,54-69.
DOI |
| 74 | USHIJIMA-MWESIGWA H, NEGRE C F A, MNISZEWSKI S M. Graph partitioning using quantum annealing on the D-Wave system[C]//Proceedings of the Second International Workshop on Post Moores Era Supercomputing. Denver, CO, USA: Association for Computing Machinery, 2017: 22-29. |
| 75 | HARIKRISHNAKUMAR R, NANNAPANENI S, NGUYEN N H, et al. A quantum annealing approach for dynamic multi-depot capacitated vehicle routing problem[EB/OL]. (2020-05-27)[2023-05-11]. https://doi.org/10.48550/arXiv.2005.12478. |
| 76 | SRINIVASAN K, SATYAJIT S, BEHERA B K, et al. Efficient quantum algorithm for solving travelling salesman problem: An IBM quantum experience[EB/OL]. (2018-05-28)[2023-05-11]. https://doi.org/10.48550/arXiv.1805.10928. |
| 77 |
NATH R K , THAPLIYAL H , HUMBLE T S .A review of machine learning classification using quantum annealing for real-world applications[J].SN Computer Science,2021,2(5):365.
DOI |
| 78 |
FARHI E , GUTMANN S .Quantum computation and decision trees[J].Physical Review A,1998,58(2):915-928.
DOI |
| 79 |
AMBAINIS A .Quantum walks and their algorithmic applications[J].International Journal of Quantum Information,2003,1(4):507-518.
DOI |
| 80 | CHILDS A M , FARHI E , GUTMANN S .An example of the difference between quantum and classical random walks[J].Quantum Information Processing,2002,1(1):35-43. |
| 81 | CHILDS A M, CLEVE R, DEOTTO E, et al. Exponential algorithmic speedup by a quantum walk[C]//Proceedings of the thirty-fifth annual ACM symposium on Theory of computing. San Diego, CA, USA: Association for Computing Machinery, 2003: 59-68. |
| 82 | BRASSARD G , HØYER P , MOSCA M , et al.Quantum amplitude amplification and estimation[J].Quantum Computation and Information,2002,305,53-74. |
| 83 |
AMBAINIS A .Quantum walk algorithm for element distinctness[J].SIAM Journal on Computing,2007,37(1):210-239.
DOI |
| 84 |
BUHRMAN H , DVRR C , HEILIGMAN M , et al.Quantum algorithms for element distinctness[J].SIAM Journal on Computing,2005,34(6):1324-1330.
DOI |
| 85 |
MAGNIEZ F , SANTHA M , SZEGEDY M .Quantum algorithms for the triangle problem[J].SIAM Journal on Computing,2007,37(2):413-424.
DOI |
| 86 | CHILDS A M , EISENBERG J M .Quantum algorithms for subset finding[J].Quantum Information & Computation,2005,5(7):593-604. |
| 87 |
DVRR C , HEILIGMAN M , HØYER P .Quantum query complexity of some graph problems[J].SIAM Journal on Computing,2006,35(6):1310-1328.
DOI |
| 88 |
WIEBE N , BERRY D W , HØYER P , et al.Simulating quantum dynamics on a quantum computer[J].Journal of Physics A: Mathematical and Theoretical,2011,44(44):445308.
DOI |
| 89 |
LLOYD S , MOHSENI M , REBENTROST P .Quantum principal component analysis[J].Nature Physics,2014,10(9):631-633.
DOI |
| 90 |
REBENTROST P , MOHSENI M , LLOYD S .Quantum support vector machine for big data classification[J].Physical Review Letters,2014,113(13):130503.
DOI |
| 91 |
CONG I , DUAN Luming .Quantum discriminant analysis for dimensionality reduction and classification[J].New Journal of Physics,2016,18(7):073011.
DOI |
| 92 |
REBENTROST P , BROMLEY T R , WEEDBROOK C , et al.Quantum hopfield neural network[J].Physical Review A,2018,98(4):042308.
DOI |
| 93 |
DALLAIRE-DEMERS P L , KILLORAN N .Quantum generative adversarial networks[J].Physical Review A,2018,98(1):012324.
DOI |
| 94 | KERENIDIS I, PRAKASH A. Quantum recommendation systems[C]//8th Innovations in Theoretical Computer Science Conference (ITCS 2017). Berkeley: Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, 2017: 49: 1-49: 21. |
| 95 |
GRANT E , BENEDETTI M , CAO Shuxiang , et al.Hierarchical quantum classifiers[J].NPJ Quantum Information,2018,4(1):65.
DOI |
| 96 |
SCHULD M , BOCHAROV A , SVORE K M , et al.Circuit-centric quantum classifiers[J].Physical Review A,2020,101(3):032308.
DOI |
| 97 |
HUANG Rui , TAN Xiaoqing , XU Qingshan .Variational quantum tensor networks classifiers[J].Neurocomputing,2021,452,89-98.
DOI |
| 98 |
PARK G , HUH J , PARK D K .Variational quantum one-class classifier[J].Machine Learning: Science and Technology,2023,4(1):015006.
DOI |
| 99 |
DILIP R , LIU Yujie , SMITH A , et al.Data compression for quantum machine learning[J].Physical Review Research,2022,4(4):043007.
DOI |
| 100 |
PÉREZ-SALINAS A , CERVERA-LIERTA A , GIL-FUSTER E , et al.Data re-uploading for a universal quantum classifier[J].Quantum,2020,4,226.
DOI |
| 101 |
LAROSE R , COYLE B .Robust data encodings for quantum classifiers[J].Physical Review A,2020,102(3):032420.
DOI |
| 102 |
CHEN S Y C , HUANG C M , HSING C W , et al.An end-to-end trainable hybrid classical-quantum classifier[J].Machine Learning: Science and Technology,2021,2(4):045021.
DOI |
| 103 | LIU Junhua , LIM K H , WOOD K L , et al.Hybrid quantum-classical convolutional neural networks[J].Science China Physics, Mechanics & Astronomy,2021,64(9):290311. |
| 104 |
HUR T , KIM L , PARK D K .Quantum convolutional neural network for classical data classification[J].Quantum Machine Intelligence,2022,4(1):3.
DOI |
| 105 |
SCHULD M , FINGERHUTH M , PETRUCCIONE F .Implementing a distance-based classifier with a quantum interference circuit[J].Europhysics Letters,2017,119(6):60002.
DOI |
| 106 |
JOHRI S , DEBNATH S , MOCHERLA A , et al.Nearest centroid classification on a trapped ion quantum computer[J].NPJ Quantum Information,2021,7(1):122.
DOI |
| 107 |
CINCIO L , SUBASI Y , SORNBORGER A T , et al.Learning the quantum algorithm for state overlap[J].New Journal of Physics,2018,20(11):113022.
DOI |
| 108 |
CEREZO M , POREMBA A , CINCIO L , et al.Variational quantum fidelity estimation[J].Quantum,2020,4,248.
DOI |
| 109 | CHEN H , WOSSNIG L , SEVERINI S , et al.Universal discriminative quantum neural networks[J].Quantum Machine Intelligence,2020,3(1):1. |
| 110 |
KARDASHIN A S , VLASOVA A V , PERVISHKO A A , et al.Quantum-machine-learning channel discrimination[J].Physical Review A,2022,106(3):032409.
DOI |
| 111 |
OHZEKI M , NISHIMORI H .Quantum annealing: an introduction and new developments[J].Journal of Computational and Theoretical Nanoscience,2011,8(6):963-971.
DOI |
| 112 |
FARHI E , GOLDSTONE J , GUTMANN S , et al.A quantum adiabatic evolution algorithm applied to random instances of an NP-complete problem[J].Science,2001,292(5516):472-475.
DOI |
| 113 | NEVEN H, DENCHEV V S, DREW-BROOK M, et al. Nips 2009 demonstration: Binary classification using hardware implementation of quantum annealing[EB/OL]. [2023-05-12]. https://api.semanticscholar.org/CorpusID:59263234. |
| 114 |
FENG Yuan , YU Nengkun , YING Mingsheng .Model checking quantum Markov chains[J].Journal of Computer and System Sciences,2013,79(7):1181-1198.
DOI |
| 115 | TANG E. A quantum-inspired classical algorithm for recommendation systems[C]//Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing. Phoenix, AZ, USA: Association for Computing Machinery, 2019: 217-228. |
| 116 |
TANG E .Quantum principal component analysis only achieves an exponential speedup because of its state preparation assumptions[J].Physical Review Letters,2021,127(6):060503.
DOI |
| 117 | CHIA N H, LIN H H, WANG Chunhao. Quantum-inspired sublinear classical algorithms for solving low-rank linear systems[EB/OL]. (2018-11-12)[2023-05-12]. https://doi.org/10.48550/arXiv.1811.04852. |
| 118 | WANG Guoming .Efficient quantum algorithms for analyzing large sparse electrical networks[J].Quantum Information & Computation,2017,17(11/12):987-1026. |
| 119 | BELOVS A. Quantum walks and electric networks[EB/OL]. (2013-02-13)[2023-05-12]. https://doi.org/10.48550/arXiv.1302.3143. |
| 120 |
Google AI Quantum and Collaborators , ARUTE F , ARYA K , et al.Hartree-Fock on a superconducting qubit quantum computer[J].Science,2020,369(6507):1084-1089.
DOI |
| 121 | CHIACCHIO E I R. Implementing real-world optimisation use cases in state-of-the-art quantum devices[EB/OL]. (2022-11-07)[2023-05-12]. https://entropicalabs.com/news/2022-11-implementing-real-world-optimisation-use-cases-in-state-of-the-art-quantum-devices/. |
| 122 | ANSCHUETZ E, OLSON J, ASPURU-GUZIK A, et al. Variational quantum factoring[C]//QTOP 2019: Quantum Technology and Optimization Problems. Munich, Germany: Springer, 2019: 74-85. |
| 123 |
LLOYD S .Universal quantum simulators[J].Science,1996,273(5278):1073-1078.
DOI |
| 124 | AHARONOV D, TA-SHMA A. Adiabatic quantum state generation and statistical zero knowledge[C]//Proceedings of the thirty-fifth annual ACM symposium on Theory of computing. San Diego, CA, USA: Association for Computing Machinery, 2003: 20-29. |
| 125 |
BERRY D W , AHOKAS G , CLEVE R , et al.Efficient quantum algorithms for simulating sparse Hamiltonians[J].Communications in Mathematical Physics,2007,270(2):359-371.
DOI |
| 126 |
COLE R , VISHKIN U .Deterministic coin tossing with applications to optimal parallel list ranking[J].Information and Control,1986,70(1):32-53.
DOI |
| 127 |
LINIAL N .Locality in distributed graph algorithms[J].SIAM Journal on Computing,1992,21(1):193-201.
DOI |
| 128 | BERRY D W , CHILDS A M .Black-box Hamiltonian simulation and unitary implementation[J].Quantum Information & Computation,2012,12(1/2):29-62. |
| 129 | BERRY D W, CHILDS A M, CLEVE R, et al. Exponential improvement in precision for simulating sparse Hamiltonians[C]//Proceedings of the forty-sixth annual ACM symposium on Theory of computing. New York: Association for Computing Machinery, 2014: 283-292. |
| 130 |
KIRBY W M , LOVE P J .Variational quantum eigensolvers for sparse hamiltonians[J].Physical Review Letters,2021,127(11):110503.
DOI |
| 131 | HUANG C, NI Xiaotong, ZHANG Fang, et al. Alibaba cloud quantum development platform: Surface code simulations with crosstalk[EB/OL]. (2020-02-20)[2023-05-12]. https://doi.org/10.48550/arXiv.2002.08918. |
| 132 | ZHANG Fang, HUANG C, NEWMAN M, et al. Alibaba cloud quantum development platform: Large-scale classical simulation of quantum circuits[EB/OL]. (2019-09-05)[2023-05-12]. https://doi.org/10.48550/arXiv.1907.11217. |
| 133 |
ZHANG Shixin , ALLCOCK J , WAN Zhouquan , et al.TensorCircuit: A quantum software framework for the NISQ era[J].Quantum,2023,7,912.
DOI |
| 134 | DOU Menghan, ZOU Tianrui, FANG Yuan, et al. QPanda: High-performance quantum computing framework for multiple application scenarios[EB/OL]. (2022-12-29)[2023-05-12]. https://doi.org/10.48550/arXiv.2212.14201. |
| 135 |
GEMME G , GROSSI M , FERRARO D , et al.IBM quantum platforms: A quantum battery perspective[J].Batteries,2022,8(5):43.
DOI |
| 136 | 饶欣欣, 李卓瑛, 宋潇, 等.离子阱量子计算机的发展现状与趋势[J].世界科技研究与发展,2022,44(2):157-171. |
| 137 |
ZHONG Hansen , WANG Hui , DENG Yuhao , et al.Quantum computational advantage using photons[J].Science,2020,370(6523):1460-1463.
DOI |
| 138 |
KIM Y , EDDINS A , ANAND S , et al.Evidence for the utility of quantum computing before fault tolerance[J].Nature,2023,618(7965):500-505.
DOI |
| [1] | 马颖, 田维坚, 樊养余. 基于云模型的自适应量子免疫克隆算法[J]. 计算物理, 2013, 30(4): 627-632. |
| [2] | 李盼池, 王琪超, 施光尧. 基于Bloch球面搜索的量子粒子群优化算法[J]. 计算物理, 2013, 30(3): 454-462. |
| [3] | 李盼池, 李士勇. 加权量子搜索算法及其相位匹配条件研究[J]. 计算物理, 2008, 25(5): 623-630. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||
版权所有 © 《计算物理》编辑部
地址:北京市海淀区丰豪东路2号 邮编:100094 E-mail:jswl@iapcm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发
