磁控忆阻器耦合Hindmarsh-Rose神经元模型及其在DNA图像加密中的应用

doi:10.19596/j.cnki.1001-246x.8850

摘要/Abstract

摘要：

提出一种磁控忆阻器模型, 建立磁感应耦合Hindmarsh-Rose(HR)神经元模型。通过分岔图、李雅普诺夫指数谱、相位图以及时序图对所构建的神经元模型进行非线性动力学分析, 进而将模型所产生的混沌序列应用于DNA混沌图像加密算法。实验结果表明: 这种电磁感应HR神经元模型在磁感应强度的影响下能够产生多种放电模式和复杂的混沌行为, 并且基于该模型产生的混沌序列具有随机性, 初值敏感性, 遍历性等特点, 应用于混沌图像加密算法中具有较强的安全性。为理解神经元隐藏动力学机制和构建忆阻器神经元网络提供支持, 对神经元相关的病变治疗具有价值。

关键词: 忆阻器, Hindmarsh-Rose神经元, DNA序列, 混沌图像加密

Abstract:

Memristor coupled neurons have complex nonlinear dynamic behavior and have been widely used in neural computing and chaotic systems. In this paper, a new magnetic controlled memristor model is proposed, and the Hindmarsh-Rose(HR) neuron model is established. The neural model is analyzed by bifurcating diagram, Lyapunov exponent spectrum, phase diagram and time series diagram. Then the chaotic sequence generated by the model is applied to the DNA chaotic image encryption algorithm. The experimental results show that this HR neuron model can generate multiple discharge modes and complex chaotic behavior under the influence of magnetic induction intensity, and the generated chaotic sequences based on the model have the characteristics of randomness, initial value sensitivity, ergodic, etc., which has strong security when applied to chaotic image encryption algorithms. These results will provide strong support for understanding the dynamics of neuron hiding and constructing memristor neural network, and have great application value for the treatment of neuron-related lesions.

Key words: memristor, Hindmarsh-Rose neurons, DNA sequence, chaotic image encryption

赵益波, 杨清, 于程程, 刘明华. 磁控忆阻器耦合Hindmarsh-Rose神经元模型及其在DNA图像加密中的应用[J]. 计算物理, 2025, 42(2): 232-242.

Yibo ZHAO, Qing YANG, Chengcheng YU, Minghua LIU. Novel Magnetron Memristor Coupled Hindmarsh-Rose Neuron Model and Its DNA Image Application in Encryption[J]. Chinese Journal of Computational Physics, 2025, 42(2): 232-242.

图/表 12

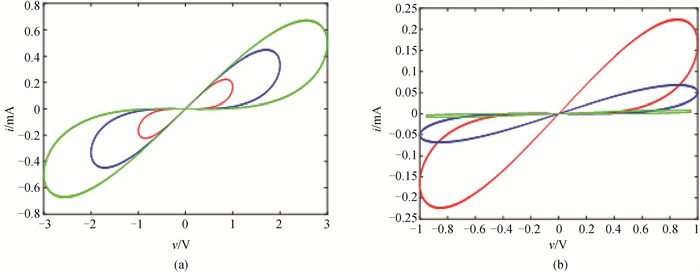
图1 忆阻器的紧磁滞回线(a)f=1 Hz时不同幅度下的紧磁滞回线; (b)A=1 V时不同频率下的紧磁滞回线

Fig.1 Memristor tight hysteresis loop (a) pinched hysteresis at different amplitudes with f=1 Hz; (b) pinched hysteresis loops at different frequencies with A=1 V

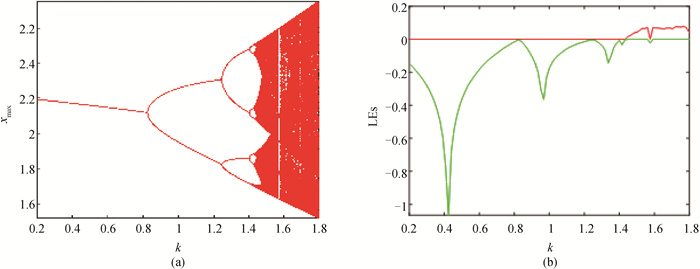
图2 磁感应强度参数k∈(0.2, 1.8)变化时的动力学状态分布(a)分岔图；(b)李雅普诺夫指数谱

Fig.2 Dynamic state distribution with change of k∈(0.2, 1.8) (a) bifurcation diagram; (b) Lyapunov exponents

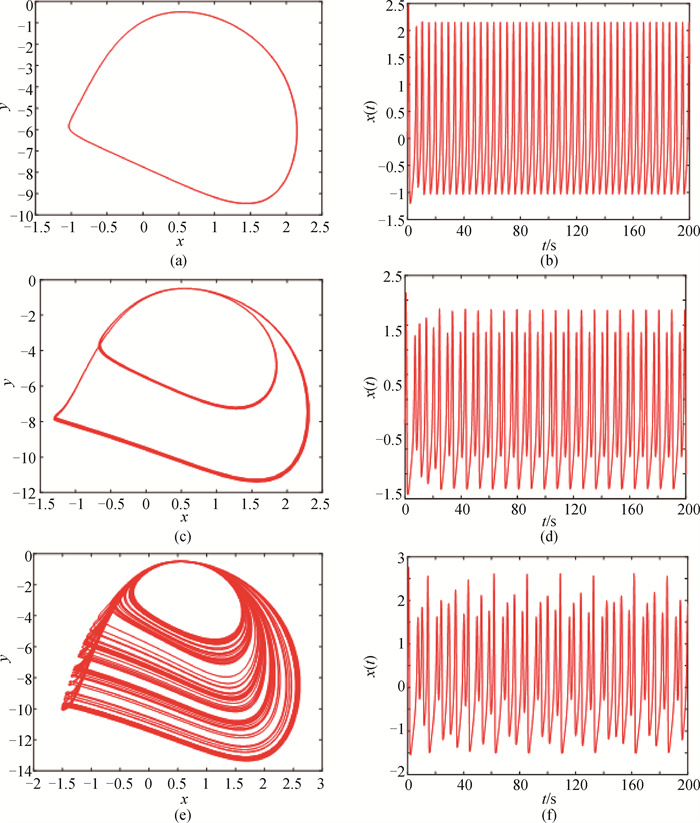
图3 不同磁感应强度k的吸引子和对应的膜电位时序图(a)吸引子，k=0.6; (b)膜电位时序图，k=0.6;(c)吸引子，k=1.2; (d)膜电位时序图，k=1.2; (e)吸引子，k=1.6; (f)膜电位时序图，k=1.6

Fig.3 Time series diagram of attractors and corresponding membrane potential for different magnetic induction intensities k (a) attractor with k=0.6; (b) potential sequence diagram with k=0.6; (c) attractor with k=1.2; (d) potential sequence diagram with k=1.2; (e) attractor with k=1.6; (f) potential sequence diagram with k=1.6

表1 DNA编码解码方式

Table 1 DNA encoding and decoding methods

	1	2	3	4	5	6	7	8
A	00	00	01	01	10	10	11	11
T	11	11	10	10	01	01	00	00
G	01	10	00	11	00	11	01	10
C	10	01	11	00	11	00	10	01

图4 混沌DNA图像加密流程

Fig.4 Chaotic DNA image encryption process

图5 实验结果图(a)原始图像；(b)密文图像；(c)解密图像

Fig.5 Experimental result diagram (a) original image; (b) ciphertext image; (c) decrypted image

图6 直方图(a)原始图像；(b)加密图像

Fig.6 Histogram of (a) original image and (b) encrypted image

表2 Pepper图像相关系数

Table 2 Correlation coefficients of Pepper images

算法	水平	垂直	对角线	平均值
原始图像	0.977 2	0.977 5	0.954 5	0.969 7
本文	-0.002 4	-0.009 5	0.003 6	0.005 2
Ref.[33]	0.016 8	0.044 5	-0.002 2	0.021 2
Ref.[34]	0.002 8	0.009 6	0.006 2	0.006 2
Ref.[35]	0.014 0	0.014 3	0.014 6	0.014 3
Ref.[36]	0.007 8	0.005 8	-0.016 4	0.010 0

表3 原始图像与密文图像信息熵

Table 3 Information entropy between original image and ciphertext image

通道	R	G	B
原始图像	7.268 2	7.590 1	6.995 1
加密图像	7.999 3	7.999 3	7.999 3

图7 加入不同密度椒盐噪声的解密图像，密度为(a) 0.005；(b) 0.01；(c) 0.05；(d) 0.1

Fig.7 Decrypted images of added salt and pepper noise with different densities (a) 0.005; (b) 0.01; (c) 0.05; (d) 0.1

图8 遮挡攻击实验结果(a) 数据丢失1/16; (b) 数据丢失1/8; (c)数据丢失1/4; (d)数据丢失1/2; (e)图(a)的解密结果；(f) 图(b)的解密结果; (g) 图(c)的解密结果; (h) 图(d)的解密结果

Fig.8 Experimental results of occlusion attack (a) data loss 1/16; (b) data loss 1/8 of encrypted images; (c) data loss 1/4;(d) data loss 1/2 s; (e) decryption of figure (a); (f) decryption of figure (b); (g) decryption of figure (c); (h) decryption of figure (d)

表4 不同算法的时间

Table 4 Time of different algorithms

算法	图像	加密时间/s
本文	Pepper	2.577 2
Ref.[37]	Babbon	5.785 5
Ref.[38]	Lena	9.182 7
Ref.[39]	Lena	4.392 0

参考文献 39

1	陈墨, 陈成杰, 包伯成, 等. 忆阻突触耦合Hopfield神经网络的初值敏感动力学[J]. 电子与信息学报, 2020, 42(4): 870- 877.
2	HODGKIN A L, HUXLEY A F. A quantitative description of membrane current and its application to conduction and excitation in nerve[J]. The Journal of Physiology, 1952, 117(4): 500- 544. DOI
3	彭建华, 于洪洁, 刘延柱. Fitz Hugh-Nagumo神经元网络的联想记忆与分割[J]. 计算物理, 2005, 22(4): 337- 343. DOI
4	MORRIS C, LECAR H. Voltage oscillations in the barnacle giant muscle fiber[J]. Biophysical Journal, 1981, 35(1): 193- 213. DOI
5	CHAYT R. Chaos in a three-variable model of an excitable cell[J]. Physica D: Nonlinear Phenomena, 1985, 16(2): 233- 242. DOI
6	代志伟, 韦笃取. 电磁辐射下正切型忆阻HR神经网络的动力学研究[J]. 计算物理, 2025, 42(2): 243- 252.
7	王春华, 蔺海荣, 孙晶如, 等. 基于忆阻器的混沌、存储器及神经网络电路研究进展[J]. 电子与信息学报, 2020, 42(4): 795- 810.
8	ZHANG Sen, ZHENG Jiahao, WANG Xiaoping, et al. Multi-scroll hidden attractor in memristive HR neuron model under electromagnetic radiation and its applications[J]. Chaos, 2021, 31(1): 011101. DOI
9	BAO Han, HUA Zhongyun, LIU Wenbo, et al. Discrete memristive neuron model and its interspike interval-encoded application in image encryption[J]. Science China Technological Sciences, 2021, 64(10): 2281- 2291. DOI
10	LIN Hairong, WANG Chunhua, SUN Yichuang, et al. Firing multistability in a locally active memristive neuron model[J]. Nonlinear Dynamics, 2020, 100(4): 3667- 3683. DOI
11	LAI Qiang, LAI Cong, ZHANG Hui, et al. Hidden coexisting hyperchaos of new memristive neuron model and its application in image encryption[J]. Chaos, Solitons, and Fractals, 2022, 158, 112017. DOI
12	BAO Bocheng, HU Aihuang, BAO Han, et al. Three-Dimensional memristive hindmarsh-rose neuron model with hidden coexisting asymmetric behaviors[J]. Complexity, 2018, 2018, 3872573. DOI
13	BAO Han, HU Aihuang, LIU Wenbo, et al. Hidden bursting firings and bifurcation mechanisms in memristive neuron model with threshold electromagnetic induction[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(2): 502- 511. DOI
14	BAO Han, ZHANG Yunzhen, LIU Wenbo, et al. Memristor synapse-coupled memristive neuron network: synchronization transition and occurrence of chimera[J]. Nonlinear Dynamics, 2020, 100(1): 937- 950. DOI
15	TAN Yumei, WANG Chunhua. A simple locally active memristor and its application in HR neurons[J]. Chaos, 2020, 30(5): 053118. DOI
16	LI Zhijun, ZHOU Haiyan, WANG Mengjiao, et al. Coexisting firing patterns and phase synchronization in locally active memristor coupled neurons with HR and FN models[J]. Nonlinear Dynamics, 2021, 104(2): 1455- 1473. DOI
17	ZHANG Sen, ZHENG Jiahao, WANG Xiaoping, et al. A novel no-equilibrium HR neuron model with hidden homogeneous extreme multistability[J]. Chaos, Solitons, & Fractals, 2021, 145, 110761.
18	唐利红, 贺宗梅, 姚延立. 具有隐藏超级多稳定性的磁感应HR神经元及其电路实现[J]. 计算物理, 2022, 39(5): 589- 597. DOI
19	孙亮, 罗佳, 乔印虎. 局部有源忆阻器电路及其在HR耦合神经元网络中的应用[J]. 电子与信息学报, 2021, 43(11): 3374- 3383. DOI
20	LI Chengqing, ZHANG Yun, XIE E Y. When an attacker meets a cipher-image in 2018: A year in review[J]. Journal of Information Security and Applications, 2019, 48, 102361. DOI
21	YILDIRIM M. Optical color image encryption scheme with a novel DNA encoding algorithm based on a chaotic circuit[J]. Chaos Solitons & Fractals, 2022, 155, 111631.
22	WU Jiahui, LIAO Xiaofeng, YANG Bo. Image encryption using 2D Hénon-Sine map and DNA approach[J]. Signal Processing, 2018, 153, 11- 23. DOI
23	YANG Chunxiao, TARALOVA I, EL ASSAD S, et al. Image encryption based on fractional chaotic pseudo-random number generator and DNA encryption method[J]. Nonlinear Dynamics, 2022, 109(3): 2103- 2127. DOI
24	ZHAO Yibo, MENG Ruoyu, ZHANG Yi, et al. Image encryption algorithm based on a new chaotic system with Rubik's cube transform and Brownian motion model[J]. Optik, 2023, 273, 170342. DOI
25	SHI Hang, YAN Dengwei, WANG Lidan, et al. A novel memristor-based chaotic image encryption algorithm with Hash process and S-box[J]. The European Physical Journal Special Topics, 2021, 231, 465- 480.
26	DONG C E. Constructing a discrete memristor chaotic mapand application to hash function with dynamic S-Box[J]. The European Physical Journal, 2022, 231, 3239- 3247.
27	SUN Junwei, YANG Qinfei, WANG Yanfeng. Dynamical analysis of novel memristor chaotic system and DNA encryption application[J]. Iranian Journal of Science and Technology, Transactions of Electrical Engineering, 2020, 44(1): 449- 460. DOI
28	刘思聪, 李春彪, 李泳新. 基于指数-余弦离散混沌映射的图像加密算法研究[J]. 电子与信息学报, 2022, 44(5): 1754- 1762.
29	WU Xiangjun, WANG Kunshu, WANG Xingyuan, et al. Color image DNA encryption using NCA map-based CML and one-time keys[J]. Signal Processing, 2018, 148, 272- 287. DOI
30	夏磊. 基于四维超混沌系统的图像加密算法设计[J/OL]. 重庆工商大学学报(自然科学版). (2023-06-15)[2023-12-30]. http://kns.cnki.net/kcms/detail/50.1155.N.20230615.1116.002.html.
31	WANG Xiong, ÇAVUSOǦLU Ü, KACAR S, et al. S-Box based image encryption application using a chaotic system without equilibrium[J]. Applied Sciences, 2019, 9(4): 781. DOI
32	赵双, 陈湘军, 张云贞. 忆阻Lorenz混沌系统的动力学分析与电路实现[J]. 计算物理, 2024, 41(2): 268- 276. DOI
33	KADIR A, HAMDULLA A, GUO Wenqiang. Color image encryption using skew tent map and hyper chaotic system of 6th-order CNN[J]. Optik, 2014, 125(5): 1671- 1675. DOI
34	LI Chunmeng, YANG Xxiaozhong. An image encryption algorithm based on discrete fractional wavelet transform and quantum chaos[J]. Optik, 2022, 260, 169042. DOI
35	PREISHUBER M, HÜTTER T, KATZENBEISSER S, et al. Depreciating motivation and empirical security analysis of chaos-based image and video encryption[J]. IEEE Transactions on Information Forensics and Security, 2018, 13(9): 2137- 2150. DOI
36	ZHOU Shihua. A real-time one-time pad DNA-chaos image encryption algorithm based on multiple keys[J]. Optics & Laser Technology, 2021, 143, 107359.
37	HUANG Zhiwen, ZHOU Nanrun. Image encryption scheme based on discrete cosine stockwell transform and DNA-level modulus diffusion[J]. Optics & Laser Technology, 2022, 149, 107879.
38	ZHAN Kun, WEI Dong, SHI Jinhui, et al. Cross-utilizing hyperchaotic and DNA sequences for image encryption[J]. Journal of Electronic Imaging, 2017, 26(1): 013021. DOI
39	WANG Xingyuan, LIU Chuanming. A novel and effective image encryption algorithm based on chaos and DNA encoding[J]. Multimedia Tools and Applications, 2017, 76(5): 6229- 6245. DOI

[1]	代志伟, 韦笃取. 电磁辐射下正切型忆阻Hindmarsh-Rose神经网络的动力学研究[J]. 计算物理, 2025, 42(2): 243-252.
[2]	黄微, 韦笃取. 电磁场耦合下Hindmarsh-Rose忆阻神经网络相干共振研究[J]. 计算物理, 2025, 42(1): 98-105.
[3]	陈吉, 徐毅, 刘进福, 刘涛. 呈现超级多稳态忆阻系统的动力学与实现[J]. 计算物理, 2024, 41(4): 523-534.
[4]	赵双, 陈湘军, 张云贞. 忆阻Lorenz混沌系统的动力学分析与电路实现[J]. 计算物理, 2024, 41(2): 268-276.
[5]	刘丽君, 韦笃取. 忆阻Rulkov神经网络同步研究[J]. 计算物理, 2023, 40(3): 389-400.
[6]	孙亮, 罗佳, 乔印虎. 忆阻Hopfield神经网络的初值位移调控动力学及其图像加密应用[J]. 计算物理, 2023, 40(1): 106-116.
[7]	唐利红, 贺宗梅, 姚延立. 具有隐藏超级多稳定性的磁感应HR神经元及其电路实现[J]. 计算物理, 2022, 39(5): 589-597.
[8]	唐利红, 贺宗梅, 姚延立. 忆阻Hopfield神经网络动力学分析及其电路实现[J]. 计算物理, 2022, 39(2): 244-252.
[9]	罗佳, 孙亮, 乔印虎. 忆阻突触耦合环形Hopfield神经网络动力学分析及其电路实现[J]. 计算物理, 2022, 39(1): 109-117.
[10]	黄志精, 白婧, 唐国宁. 单向耦合神经元网络中螺旋波的自发形成机制[J]. 计算物理, 2020, 37(5): 612-622.
[11]	王伟, 曾以成, 陈争, 孙睿婷. 忆阻器混沌电路产生的共存吸引子与Hopf分岔[J]. 计算物理, 2017, 34(6): 747-756.
[12]	余世成, 曾以成, 李志军. 一种二次型忆阻器四阶混沌电路[J]. 计算物理, 2015, 32(6): 735-743.
[13]	谭志平, 杨红姣, 刘奇能, 曾以成. 最简荷控型忆阻器混沌电路的设计及实现[J]. 计算物理, 2015, 32(4): 496-504.