计算物理 ›› 2024, Vol. 41 ›› Issue (5): 559-568.DOI: 10.19596/j.cnki.1001-246x.8859
收稿日期:2023-11-01
出版日期:2024-09-25
发布日期:2024-09-14
通讯作者:
陈军
作者简介:徐云, 女, 博士, 副研究员, 研究方向为有限元方法、多尺度方法, E-mail: xu_yun@iapcm.ac.cn
基金资助:
Yun XU( ), Yao LONG, Meizhen XIANG, Jun CHEN(
), Yao LONG, Meizhen XIANG, Jun CHEN( )
)
Received:2023-11-01
Online:2024-09-25
Published:2024-09-14
Contact:
Jun CHEN
摘要:
考虑到夹杂-基体界面微结构复杂失效过程对非均质PBX(高聚物黏结炸药)材料损伤起始具有主导作用, 本文提出基于Eshelby夹杂理论的相场损伤模型, 对非均质PBX炸药损伤形核演化进行数值模拟。相场能量由弹性能和夹杂-基体相互作用能构成, 结合Mori-Tanaka方法推导不同级配下PBX炸药等效力学模量, 相场内变量的变化直接反映了非线性脱黏效应下的损伤分布。采用Eshelby夹杂理论相场方法计算高模量比非均质PBX炸药圆形和多边形颗粒夹杂典型结构, 分析加载条件、颗粒形状、体积占比、模型参数对夹杂-基体界面脱黏机制的影响。数值结果表明: 夹杂-基体界面微结构演化加速了界面脱黏与宏观损伤的形成, 与实验观测是一致的。
中图分类号:
徐云, 龙瑶, 向美珍, 陈军. 非均质炸药的Eshelby夹杂理论相场方法[J]. 计算物理, 2024, 41(5): 559-568.
Yun XU, Yao LONG, Meizhen XIANG, Jun CHEN. Phase-Field Fracture Method Based on Eshelby Theory for Heterogeneous PBX[J]. Chinese Journal of Computational Physics, 2024, 41(5): 559-568.
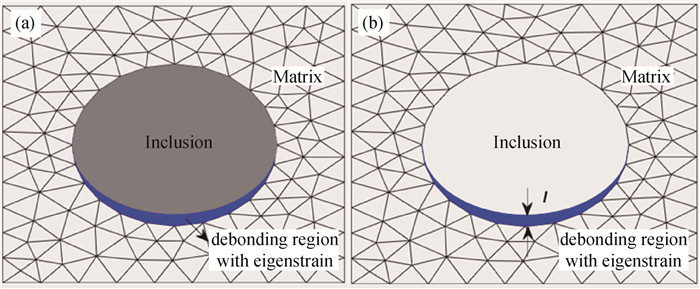
图1 采用Eshelby本征应变表征夹杂相场模型的脱黏区(a)采用本征应变表征脱黏区;(b)引入长度尺度
Fig.1 Debonding of the inclusion phase field model is characterized by Eshelby's eigenstrain (a) debonding region is characterized by eigenstrain; (b) introduce a length scale
| 杨氏模量/GPa | 剪切模量/GPa | 能量释放率/(J·m-2) | 泊松比 | |
| 夹杂颗粒 | 32.45 | 14.19 | 3.50 | 0.143 3 |
| 粘结剂 | 2.40 | 0.80 | 1.02 | 0.499 5 |
| 等效模量 | 7.39 | 2.47 | 1.16 | 0.499 1 |
表1 非均质PBX材料计算参数
Table 1 Computational parameters of heterogeneous PBX
| 杨氏模量/GPa | 剪切模量/GPa | 能量释放率/(J·m-2) | 泊松比 | |
| 夹杂颗粒 | 32.45 | 14.19 | 3.50 | 0.143 3 |
| 粘结剂 | 2.40 | 0.80 | 1.02 | 0.499 5 |
| 等效模量 | 7.39 | 2.47 | 1.16 | 0.499 1 |
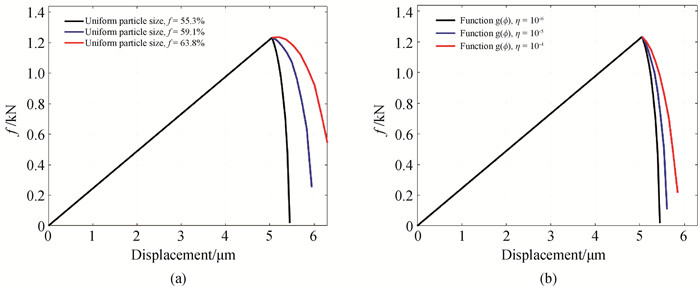
图2 计算模型的位移-力加载条件(a)不同的夹杂体积占比;(b)不同的相场递降函数计算参数
Fig.2 Force-displacement loading condition for the computational model with (a) different inclusion volume fractions and (b) different computational parameters in the phase field degradation functions
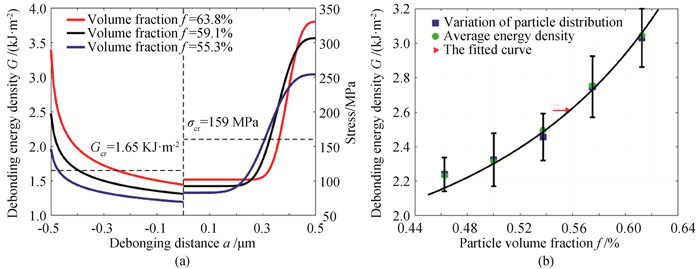
图10 脱黏强度与夹杂体积占比和微结构分布的关系(a)临界脱黏能量和应力;(b)随着夹杂体积占比的变化关系
Fig.10 Relationship between debonding and energy density and inclusion volume fraction and microstructure (a) critical debonding energy and critical stress; (b) inclusion volume fraction
| 1 |
BALZER J , SIVIOUR C , WALLEY S , et al. Behaviour of ammonium perchlorate-based propellants and a polymer-bonded explosive under impact loading[J]. Proceedings of the Royal Society A-Mathematical Physical and Engineering Sciences, 2004, 460 (2043): 781- 806.
DOI |
| 2 |
BENNETT J G , HABERMAN K S , JOHNSON J N , et al. A constitutive model for the non-shock ignition and mechanical response of high explosives[J]. Journal of the Mechanics and Physics of Solids, 1998, 46 (12): 2303- 2322.
DOI |
| 3 |
LACONDEMINE T , ROUX-LANGLOIS C , ROUXEL T . Role of poisson's ratio mismatch on the crack path in glass matrix particulate composites[J]. International Journal of Fracture, 2017, 207 (1): 73- 85.
DOI |
| 4 |
TAN H , HUANG Y , LIU C , et al. The Mori–tanaka method for composite materials with nonlinear interface debonding[J]. International Journal of Plasticity, 2005, 21 (10): 1890- 1918.
DOI |
| 5 |
DIENES J K , ZUO Q H , KERSHNER J D . Impact initiation of explosives and propellants via statistical crack mechanics[J]. Journal of the Mechanics and Physics of Solids, 2006, 54 (6): 1237- 1275.
DOI |
| 6 |
KIM S , WEI Yaochi , HORIE Y , et al. Prediction of shock initiation thresholds and ignition probability of polymer-bonded explosives using mesoscale simulations[J]. Journal of the Mechanics and Physics of Solids, 2018, 114, 97- 116.
DOI |
| 7 |
LIU Ming , HUANG Xicheng , WU Yaoqing , et al. Numerical simulations of the damage evolution for plastic-bonded explosives subjected to complex stress states[J]. Mechanics of Materials, 2019, 139, 103179.
DOI |
| 8 |
BRANCO R , ANTUNES F V , COSTA J D . A review on 3D-FE adaptive remeshing techniques for crack growth modeling[J]. Engineering Fracture Mechanics, 2015, 141, 170- 195.
DOI |
| 9 |
BRISARD S , SAB K , DORMIEUX L . New boundary conditions for the computation of the apparent stiffness of statistical volume elements[J]. Journal of the Mechanics and Physics of Solids, 2013, 61 (12): 2638- 2658.
DOI |
| 10 |
KIKUCHI M , WADA Y , SHINTAKU Y , et al. Fatigue crack growth simulation in heterogeneous material using s-version FEM[J]. International Journal of Fatigue, 2014, 58, 47- 55.
DOI |
| 11 |
BELYTSCHKO T , BLACK T . Elastic crack growth in finite elements with minimal remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 45 (5): 601- 620.
DOI |
| 12 |
HUYNH D B P , BELYTSCHKO T . The extended finite element method for fracture in composite materials[J]. International Journal for Numerical Methods in Engineering, 2009, 77 (2): 214- 239.
DOI |
| 13 |
GAO Yue , LIU Zhanli , WANG Tao , et al. Crack forbidden area in the anisotropic fracture toughness medium[J]. Extreme Mechanics Letters, 2018, 22, 172- 175.
DOI |
| 14 |
DUGDALE D S . Yielding of steel sheets containing slits[J]. Journal of the Mechanics and Physics of Solids, 1960, 8 (2): 100- 104.
DOI |
| 15 |
XU X P , NEEDLEMAN A . Numerical simulations of fast crack growth in brittle solids[J]. Journal of the Mechanics and Physics of Solids, 1994, 42 (9): 1397- 1434.
DOI |
| 16 | CAMACHO G T , ORTIZ M . Computational modelling of impact damage in brittle materials[J]. International Journal of Solids and Structures, 1996, 33 (20/22): 2899- 2938. |
| 17 |
FRANCFORT G A , MARIGO J J . Revisiting brittle fracture as an energy minimization problem[J]. Journal of the Mechanics and Physics of Solids, 1998, 46 (8): 1319- 1342.
DOI |
| 18 |
BOURDIN B , FRANCFORT G A , MARIGO J J . Numerical experiments in revisited brittle fracture[J]. Journal of the Mechanics and Physics of Solids, 2000, 48 (4): 797- 826.
DOI |
| 19 |
AMOR H , MARIGO J J , MAURINI C . Regularized formulation of the variational brittle fracture with unilateral contact: Numerical experiments[J]. Journal of the Mechanics and Physics of Solids, 2009, 57 (8): 1209- 1229.
DOI |
| 20 |
MIEHE C , WELSCHINGER F , HOFACKER M . Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations[J]. International Journal for Numerical Methods in Engineering, 2010, 83 (10): 1273- 1311.
DOI |
| 21 |
AMBATI M , GERASIMOV T , DE LORENZIS L . A review on phase-field models of brittle fracture and a new fast hybrid formulation[J]. Computational Mechanics, 2015, 55 (2): 383- 405.
DOI |
| 22 |
TANNE E , LI T , BOURDIN B , et al. Crack nucleation in variational phase-field models of brittle fracture[J]. Journal of the Mechanics and Physics of Solids, 2018, 110, 80- 99.
DOI |
| 23 | 冯其红, 赵蕴昌, 王森, 等. 基于相场方法的孔隙尺度油水两相流体流动模拟[J]. 计算物理, 2020, 37 (4): 439- 447. |
| 24 |
李建伟, 项璇, 王景栋, 等. 不同温度和扰动应变作用下纳米微裂纹的晶体相场研究[J]. 计算物理, 2022, 39 (6): 717- 726.
DOI |
| 25 |
王进, 马文婧, 刘玉周, 等. 非晶一次晶化过程微观组织演化和生长动力学的相场法研究[J]. 计算物理, 2022, 39 (4): 403- 410.
DOI |
| 26 |
马文婧, 王进, 郭慧, 等. 晶体相场法研究金属微互连结构形变过程对界面Kirkendall空洞生长的抑制机理[J]. 计算物理, 2023, 40 (4): 416- 424.
DOI |
| 27 |
HASHIN Z . The elastic moduli of heterogeneous materials[J]. Journal of Applied Mechanics, 1962, 29 (1): 143- 150.
DOI |
| 28 |
HASHIN Z , SHTRIKMAN S . On some variational principles in anisotropic and nonhomogeneous elasticity[J]. Journal of the Mechanics and Physics of Solids, 1962, 10 (4): 335- 342.
DOI |
| 29 |
HILL R . A self-consistent mechanics of composite materials[J]. Journal of the Mechanics and Physics of Solids, 1965, 13 (4): 213- 222.
DOI |
| 30 |
ESHELBY J . The force on an elastic singularity[J]. Philosophical Transactions of the Royal Society of London Series A, 1951, 244 (877): 87- 112.
DOI |
| 31 | ESHELBY J . The determination of the elastic field of an ellipsoidal inclusion and related problems[J]. Philosophical Transactions of the Royal Society of London. Series A, 1957, 241 (1226): 376- 396. |
| 32 |
MORI T , TANAKA K . Average stress in matrix and average elastic energy of materials with misfitting inclusions[J]. Acta Metallurgica, 1973, 21 (5): 571- 574.
DOI |
| 33 | WEINBERGER C , CAI Wei , BARNETT D . Elasticity of microscopic structures[M]. ME340B Lecture Notes, Stanford University, 2005: 43- 46. |
| 34 |
XU Yun , XIANG Meizhen , YU Jidong , et al. A variational fracture method based on Eshelby transformation[J]. European Journal of Mechanics- A/Solids, 2023, 97, 104846.
DOI |
| 35 |
MATOUŠ K , GEUBELLE P H . Multiscale modeling of particle debonding in reinforced elastomers subjected to finite deformations[J]. International Journal for Numerical Methods in Engineering, 2006, 65 (2): 190- 223.
DOI |
| 36 |
MATOUŠ K , KULKARNI M , GEUBELLE P . Multiscale cohesive failure modeling of heterogeneous adhesives[J]. Journal of the Mechanics and Physics of Solids, 2008, 56 (4): 1511- 1533.
DOI |
| [1] | 张邦文, 任忠鸣, 邓康, 钟云波. 直流电对金属液电磁净化的影响[J]. 计算物理, 2002, 19(6): 527-531. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||
版权所有 © 《计算物理》编辑部
地址:北京市海淀区丰豪东路2号 邮编:100094 E-mail:jswl@iapcm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发
