基于局部基本解法的静电场仿真分析

doi:10.19596/j.cnki.1001-246x.8308

摘要/Abstract

摘要：

将局部基本解方法应用于静电场问题的模拟与分析。局部基本解方法是利用控制方程的基本解，基于局部理论和移动最小二乘原理提出的一种无网格算法。相比于有限元和有限差分等传统网格类方法，该方法仅需离散节点，避免了复杂的网格剖分难题。作为一种半解析数值技术，物理问题的基本解被作为插值基函数建立数值离散模型，从而保证了算法的较高精度。此外，与具有全局离散格式的无网格方法相比，局部基本解法更适用于高维复杂几何和大尺度模拟。二维和三维数值试验表明，该方法具有实施方便灵活，计算精度高和计算速度快等优势。为静电场仿真研究开辟新的途径，拓展了局部基本解方法的应用领域。

关键词: 局部基本解方法, 无网格法, 静电场, 基本解

Abstract:

Localized method of fundamental solutions is applied to the simulation and analysis of electrostatic field problems. The localized method of fundamental solutions is a meshless algorithm based on local theory and moving least square approximation, which uses fundamental solution of the governing equation. Compared with traditional mesh-type methods such as finite element method and finite difference method, this method needs discrete nodes only, and avoids troublesome mesh generation. As a semi-analytical numerical technique, fundamental solutions of physical problems are used as interpolation basis functions to establish a numerical discrete model, thus ensuring high accuracy of the algorithm. In addition, compared with meshless methods with global discretization scheme, the local fundamental method is more suitable for high-dimensional complex geometry and large-scale simulation. Two- and three-dimensional numerical tests show that this method is convenient, flexible, accurate and fast. It is a new way for electrostatic field simulation. It expands application of localized method of fundamental solutions.

Key words: localized method of fundamental solutions, meshless method, electrostatic field, fundamental solution

中图分类号:

TM151

王超, 王发杰, 谷岩, 王晓. 基于局部基本解法的静电场仿真分析[J]. 计算物理, 2021, 38(5): 612-622.

Chao WANG, Fajie WANG, Yan GU, Xiao WANG. Simulation Analysis of Electrostatic Field Based on Localized Method of Fundamental Solutions[J]. Chinese Journal of Computational Physics, 2021, 38(5): 612-622.

图/表 16

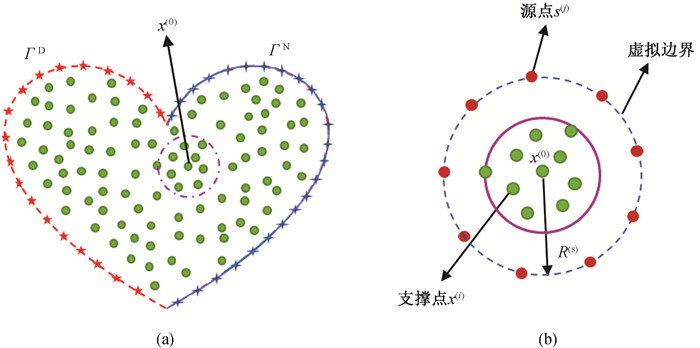
图1 静电场边值问题的LMFS示意图(a) 节点分布；(b) 局部子域

Fig.1 Schematic of the LMFS for boundary value problem of electrostatic field (a) distribution of nodes; (b) local subdomain

图2 矩形接地金属槽模型

Fig.2 Model of rectangular grounding metal slot

图3 LMFS的节点分布示意图(a) 节点均匀分布；(b) 节点不规则分布

Fig.3 Nodal distribution of the LMFS (a) regular nodal distribution; (b) irregular nodal distribution

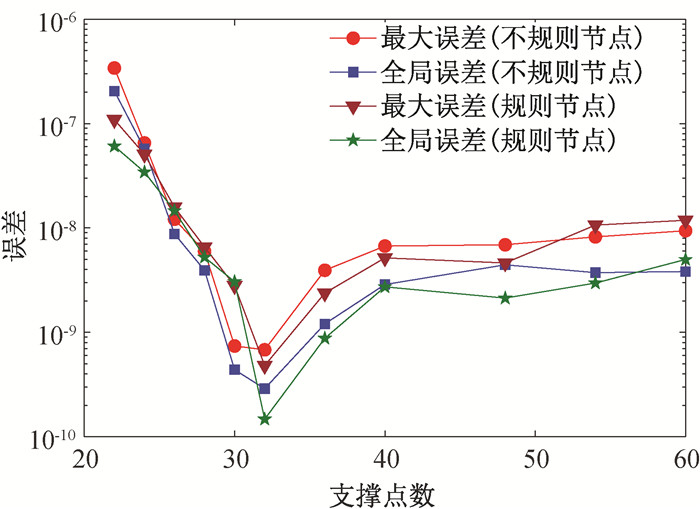
图4 规则和不规则节点分布下LMFS随支撑点数目增加的误差变化曲线

Fig.4 Error curves of the LMFS with respect to the number of supporting nodes, under regular and irregular nodal distributions

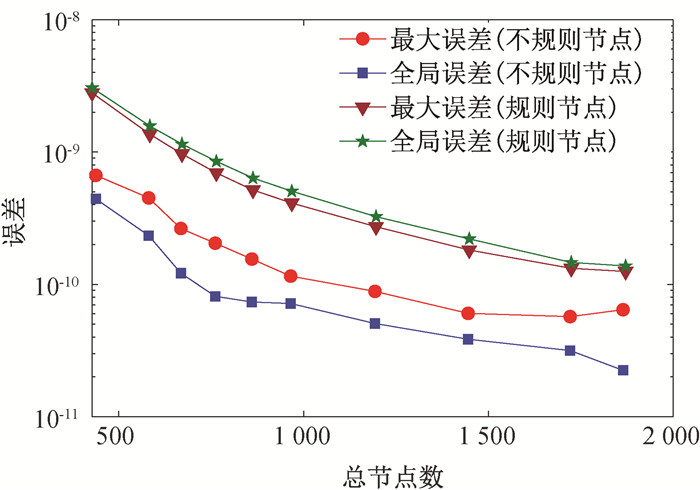
图5 规则和不规则节点分布下LMFS随总节点数目增加的误差变化曲线

Fig.5 Error curves of the LMFS with respect to the number of total nodes, under regular and irregular nodal distributions

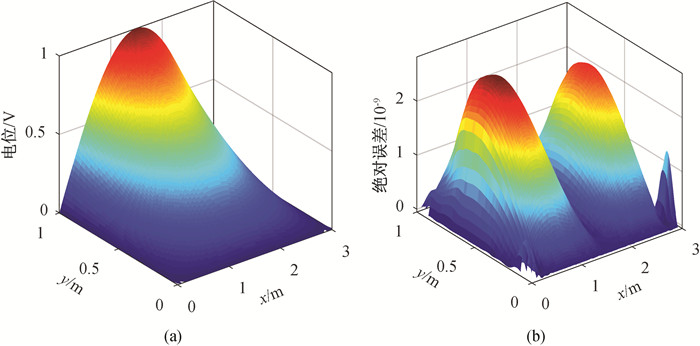
图6 计算域内电位的精确分布及数值误差(a) 精确解；(b) 绝对误差

Fig.6 Exact solution and numerical error of electric potential in the computational domain (a) exact solution; (b) absolute error

图7 LMFS、GFDM和MFS在不同节点数目下的计算时间

Fig.7 Calculation times of LMFS, GFDM and MFS with respect to the total number of nodes

图8 LMFS、GFDM和MFS在不同节点数目下的全局误差

Fig.8 Global errors of LMFS, GFDM and MFS with respect to the total number of nodes

表1 加扰动时LMFS、GFDM和MFS的计算误差

Table 1 Computational errors of MFS, LMFS and GFDM with distrubance

s/%	MFS	LMFS	GFDM
0	2.881×10^-13	3.057×10^-9	9.355×10^-6
1	7.431×10^-3	1.386×10^-3	7.576×10^-3
3	1.966×10^-2	7.725×10^-3	1.593×10^-2
5	4.117×10^-2	8.575×10^-3	4.670×10^-2

图9 FEM的网格分布

Fig.9 Mesh distribution of the FEM

图10 LMFS的节点分布

Fig.10 Nodal distribution of the LMFS

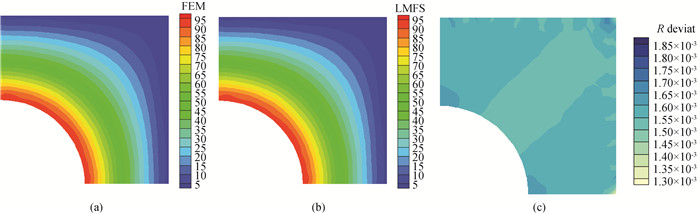
图11 方形槽电位分布(a) FEM计算结果；(b) LMFS计算结果；(c) 相对偏差分布

Fig.11 Electric potential distributions (a) results of FEM; (b) results of FEM; (c) distribution of relative deviation

图12 S型管道模型

Fig.12 An S-shape pipe model

图13 FEM网格分布

Fig.13 Distribution of FEM mesh

图14 电位仿真结果(a) FEM；(b) N=5 443；(c) N=7 649；(d) N=13 375

Fig.14 Electric potential simulation results (a) FEM; (b) N=5 443; (c) N=7 649; (d) N=13 375

表2 LMFS和GFDM的计算结果及其与FEM计算结果的比较

Table 2 Numerical results obtained with FEM, LMFS and GFDM

坐标	FEM	LMFS	LMFS偏差/10^-3	GFDM	GFDM偏差/10^-2
(0.07, 0, 0)	1.982 01	1.976 05	3.01	1.934 52	2.40
(0.2, 0, 0)	3.871 22	3.863 86	1.90	3.769 14	2.64
(0.3, 0.1, 0)	5.339 76	5.355 57	2.96	5.314 81	0.467
(0.4, 0.2, 0)	7.359 71	7.389 45	4.04	7.885 56	7.14
(0.5, 0.2, 0)	8.563 52	8.578 86	1.79	8.893 10	3.85

参考文献 34

1	DAI Guoqiang, YU Zhenhong, GAO Lei, et al. Research on finite-difference time-domain method[J]. Modern Electronics Technique, 2013, 36 (1): 140- 143.
2	ZHAO Chengfang, LI Yuehui, ZHAN Hongxia. Combined iterative method based on COCG algorithm for solving electromagnetic FEM linear equations[J]. Semiconductor Optoelectronics, 2013, 34 (4): 595- 599.
3	ZHANG Yanjun, WANG Sijing, WANG Enzhi. Analysis of two-phase continuous porous media with FEM-EFGM coupled method[J]. Chinese Journal of Computational Physics, 2003, 20 (2): 142- 146.
4	ZHANG Huaiqing, WANG Yawei, FU Zhihong. Virtual boundary element method in computational electromagnetics[J]. Transactions of China Electrotechnical Society, 2013, 28 (2): 86- 90.
5	SUN Rui, HU Zongjun, NIU Zhongrong. Analysis of nearly singular integral problem in 3D acoustic field boundary element method[J]. Chinese Journal of Computational Physics, 2017, 34 (5): 611- 618.
6	YUAN Feng, DING Ning, LI Hao, et al. An electromagnetic field prediction method in the mountains based on 3D MoM and 2D FMM[J]. Journal of Microwaves, 2018, 34 (S1): 57- 59.
7	JIN Liang, QIU Yuntao, YANG Qingxin, et al. A parallel computing method to electromagnetic problems based on cloud computing[J]. Transactions of China Electrotechnical Society, 2016, 31 (22): 5- 11.
8	QIAO Ji, ZOU Jun, YUAN Jiansheng, et al. A new finite difference based approach for calculating ion flow field of HVDC transmission lines[J]. Transactions of China Electrotechnical Society, 2015, 30 (6): 85- 91.
9	WANG Zezhong, DONG Bo, LIU Chunming, et al. Three-dimensional earth conductivity structure modelling in North China and calculation of geoelectromagnetic fields during geomagnetic disturbances based on finite element method[J]. Transactions of China Electrotechnical Society, 2015, 30 (3): 61- 66.
10	XIE Dexin, ZHU Zhanxin, WU Dongyang, et al. Plight and perspective of large-scale engineering eddy current field FEM computation[J]. Proceedings of the CSEE, 2015, 35 (5): 1250- 1257.
11	CHEN Shenshen, WANG Juan. Application of a coupled interpolating element-free Galerkin scaled boundary method and finite element method in fracture analysis of piezoelectric materials[J]. Applied Mathematics and Mechanics, 2018, 39 (11): 1258- 1267.
12	CHEN Shenshen, LIU Yinghua, CEN Zhangzhi. Shakedown analysis by using the element free Galerkin method with orthogonal basis and nonlinear programming[J]. Chinese Journal of Computational Mechanics, 2009, 26 (1): 80- 86.
13	WANG Xiaodong, OUYANG Jie, WANG Yulong, et al. Nodal integration element-free Galerkin method with upwind shifted integration nodes[J]. Chinese Journal of Computational Physics, 2012, 29 (2): 183- 190.
14	YANG Qingxin, LIU Suzhen, CHEN Haiyan. The study of some key problems in element-free Galerkin method for electromagnetic field computations[J]. Journal of Hebei University of Technology, 2004, 33 (2): 28- 34.
15	ZHANG Huaiqing, NIE Xin, WANG Yawei, et al. Application of radial basis function-virtual boundary method in electromagnetic computation[J]. Transactions of China Electrotechnical Society, 2014, 29 (4): 79- 84.
16	LIN Yanzhong, CHEN Bing, XU Xu. Radial basis function interpolation in moving mesh technique[J]. Chinese Journal of Computational Physics, 2012, 29 (2): 191- 197.
17	CHEN Wen, FU Zhuojia, CHEN C S. Recent advances in radial basis function collocation methods[M]. Heidelberg: Springer, 2014.
18	WANG Fajie, CHEN Wen, HUA Qingsong. A simple empirical formula of origin intensity factor in singular boundary method for two-dimensional Hausdorff derivative Laplace equations with Dirichlet boundary[J]. Computers & Mathematics with Applications, 2018, 76 (5): 1075- 1084.
19	WANG Fajie, CHEN Wen. Accurate empirical formulas for the evaluation of origin intensity factor in singular boundary method using time-dependent diffusion fundamental solution[J]. International Journal of Heat and Mass Transfer, 2016, 103 (1): 360- 369.
20	LI Yudong, WANG Fajie, CHEN Wen. MATLAB implementation of a singular boundary method for transient heat conduction[J]. Applied Mathematics and Mechanics, 2019, 40 (3): 259- 268.
21	CHEN Wen, SHEN L J, SHEN Z J, et al. Boundary knot method for Poisson equations[J]. Engineering Analysis with Boundary Elements, 2005, 29 (8): 756- 760. DOI
22	SHI Jinhong, FU Zhuojia, CHEN Wen. Boundary knot method for 2D transient heat conduction problems[J]. Applied Mathematics and Mechanics, 2014, 35 (2): 111- 120.
23	WANG Fajie, ZHANG Yaoming, GONG Yanpeng. Inverse identification of boudary conditions for anisotropic potential problems of thin body using MFS[J]. Engineering Mechanics, 2016, 33 (2): 18- 24.
24	CHEN C S, GOLBERG M A, HON Y C. The method of fundamental solutions and quasi-Monte-Carlo method for diffusion equations[J]. International Journal for Numerical Methods in Engineering, 1998, 43 (8): 1421- 1435. DOI
25	MARIN L, LESNIC D. The method of fundamental solutions for nonlinear functionally graded materials[J]. International Journal of Solids & Structures, 2007, 44 (21): 6878- 6890.
26	SUN Yao, MARIN L. An invariant method of fundamental solutions for two-dimensional isotropic linear elasticity[J]. International Journal of Solids & Structures, 2017, 117 (1): 191- 207.
27	ALVES C J S, ANTUNES P R S. The method of fundamental solutions applied to boundary value problems on the surface of a sphere[J]. Computers & Mathematics with Applications, 2018, 75 (7): 2365- 2373.
28	WANG Fajie, GU Yan, QU Wenzhen, et al. Localized boundary knot method and its application to large-scale acoustic problems[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 361 (1): 112729.
29	FAN Chia-Ming, HUANG Y K, CHEN C S, et al. Localized method of fundamental solutions for solving two-dimensional Laplace and biharmonic equations[J]. Engineering Analysis with Boundary Elements, 2019, 101 (1): 188- 197.
30	QU Wen, FAN Chia-Ming, GU Yan, et al. Analysis of three-dimensional interior acoustic fields by using the localized method of fundamental solutions[J]. Applied Mathematical Modelling, 2019, 76 (1): 122- 132.
31	YUE Xingxing, WANG Fajie, ZHANG Chuanzeng, et al. Localized boundary knot method for 3D inhomogeneous acoustic problems with complicated geometry[J]. Applied Mathematical Modelling, 2021, 92, 410- 421. DOI
32	GU Yan, FAN Chia-Ming, XU Rui-Ping. Localized method of fundamental solutions for large-scale modeling of two-dimensional elasticity problems[J]. Applied Mathematics Letters, 2019, 93 (1): 8- 14.
33	GU Yan, FAN Chia-Ming, QU Wenzhen, et al. Localized method of fundamental solutions for large-scale modelling of three-dimensional anisotropic heat conduction problems-Theory and MATLAB code[J]. Computers & Structures, 2019, 220 (1): 144- 155.
34	BELYTSCHKO T, KRONGAUZ Y, ORGAN D, et al. Meshless methods: An overview and recent developments[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139 (1-4): 3- 47. DOI

[1]	王磊磊, 纪乐, 马文涛. FGMs稳态热传导分析的重心Lagrange插值配点法[J]. 计算物理, 2020, 37(2): 173-181.
[2]	唐秋明, 高强. 风沙流对高压绝缘子电位和电场分布的影响[J]. 计算物理, 2016, 33(5): 539-546.
[3]	陈莘莘, 李庆华, 欧蔓丽. 中厚板弯曲问题的Kriging插值无网格法[J]. 计算物理, 2013, 30(4): 547-553.
[4]	王海涛, 曾向阳. 周期结构声散射系数的无网格数值计算方法[J]. 计算物理, 2013, 30(2): 229-236.
[5]	郑子君, 陈永强, 陈璞. 无网格方法施加本质边界条件的主从自由度法[J]. 计算物理, 2012, 29(2): 159-165.
[6]	张淮清, 俞集辉, 郑亚利. 径向基函数及其耦合方法在电磁场数值计算中的应用[J]. 计算物理, 2009, 26(2): 299-310.
[7]	强洪夫, 高巍然. 完全变光滑长度SPH法及其实现[J]. 计算物理, 2008, 25(5): 569-575.
[8]	聂玉峰, 孟卓, 樊祥阔. 三维无网格法中权函数影响半径的优化[J]. 计算物理, 2008, 25(3): 269-274.
[9]	何锃, 吕浚潮, 戴呈豪. 新型快速多极边界元法求解电荷任意分布的二维静电场[J]. 计算物理, 2007, 24(4): 433-438.
[10]	李亚莎, 王泽忠, 卢斌先. 三维静电场线性插值边界元中的解析积分方法[J]. 计算物理, 2007, 24(1): 59-64.
[11]	仇轶, 由长福, 祁海鹰, 徐旭常. 无网格方法中的背景积分方案及单颗粒下降过程的数值模拟[J]. 计算物理, 2006, 23(5): 525-529.
[12]	龙永兴, 牟宗泽, 王爱科, 董家齐. 一类奇异复本征方程组的数值计算[J]. 计算物理, 2006, 23(4): 436-440.
[13]	尹华杰, 吴建华. 无网格法剖析及基扩充EFG法在电磁计算中的应用[J]. 计算物理, 2004, 21(1): 68-76.
[14]	陈琪, 马逸尘, 应根军, 杨小斌. Poisson方程Neumann边值反问题的存在性、唯一性和稳定性[J]. 计算物理, 2001, 18(6): 531-538.
[15]	钱祥忠. 静电场对SmC^*相液晶作用的计算研究[J]. 计算物理, 1999, 16(3): 316-320.