计算物理 ›› 2022, Vol. 39 ›› Issue (2): 223-232.DOI: 10.19596/j.cnki.1001-246x.8364
收稿日期:2021-03-24
出版日期:2022-03-25
发布日期:2022-06-24
通讯作者:
郭照立, 陈松泽
作者简介:潘剑(1995-),男,硕士研究生,湖北武汉,研究方向为基于深度学习的多孔介质流动与传热,E-mail:846888172@qq.com
Jian PAN( ), Zhaoli GUO*(
), Zhaoli GUO*( ), Songze CHEN*(
), Songze CHEN*( )
)
Received:2021-03-24
Online:2022-03-25
Published:2022-06-24
Contact:
Zhaoli GUO, Songze CHEN
摘要:
提出一种名为NN-PDE(neural network-partial differential equations)的复合神经网络方法, 用于噪声数据预处理和学习偏微分方程。NN-PDE用一套神经网络负责数据预处理, 另一套网络耦合备选的方程信息, 进而学习潜在的控制方程。两套网络复合为一套网络, 可更加高效地处理噪声数据, 有效减小噪声的影响。使用NN-PDE学习多种物理方程(如Burgers方程、Korteweg-de Vries方程、Kuramoto-Sivashinsky方程和Navier-Stokes方程)的噪声数据, 均可获得准确的控制方程。
潘剑, 郭照立, 陈松泽. 从噪声数据学习偏微分方程的复合神经网络[J]. 计算物理, 2022, 39(2): 223-232.
Jian PAN, Zhaoli GUO, Songze CHEN. A Compound Neural Network for Learning Partial Differential Equations from Noisy Data[J]. Chinese Journal of Computational Physics, 2022, 39(2): 223-232.
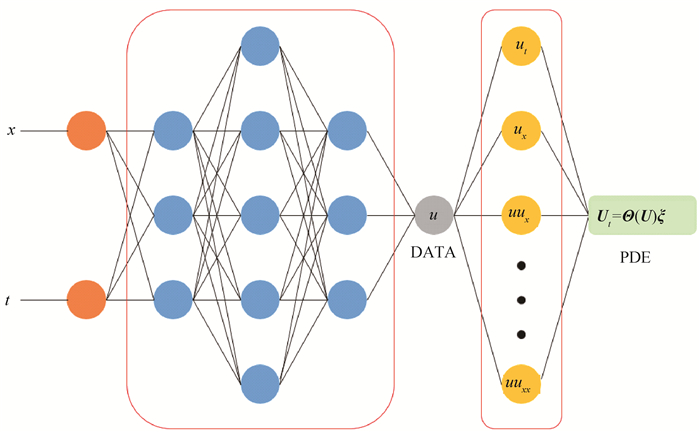
图2 复合神经网络结构(蓝色部分表示逼近方程解的网络,黄色部分表示构造的候选项,DATA部分表示数据的残差,PDE部分表示构造的控制方程残差。)
Fig.2 Structure of a compound neural network (The blue part represents the network that approximates solution of the equation. The yellow part represents the constructed candidate library. The DATA part represents residual of the data. The PDE part represents residual of the constructed governing equation.)
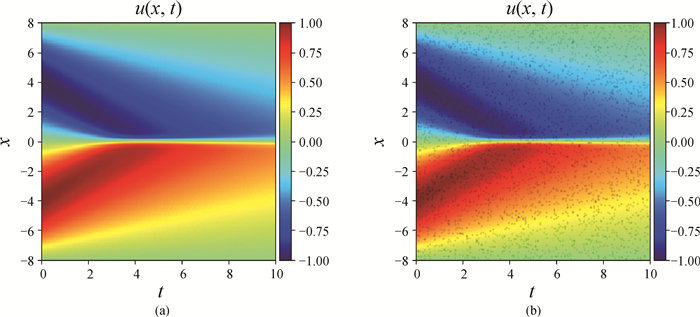
图3 (a) Burgers方程解u的云图;(b) 图中一部分代表从数据中随机选择的3000组 (背景为解u的云图,黑点是选择的数据。)
Fig.3 (a) Solution of Burgers equation in the form of heat map and (b) a portion of the map indicating 3000 data selected randomly from the dataset (The background represents the solution u in the dataset by heat map, and the black dots are selected data.)
| 噪声数据量 | NN-PDE | STRidge |
| 无 | ut=- 0.9988 uux+0.0999 uxx | ut=- 1.001 uux+0.102 uxx |
| 1% | ut=- 0.9965 uux+0.0997 uxx | ut=- 0.960 uux+0.102 uxx |
| 5% | ut=- 0.9992 uux+0.1003 uxx | ut=- 0.824 uux+0.117 uxx - 0.06 u2uxx |
| 10% | ut=- 0.9789 uux+0.0998 uxx | 无法得到简约的方程 |
表1 Burgers方程ut=- uux+0.1uxx在不同噪声中NN-PDE和STRidge的性能
Table 1 Performance of NN-PDE and STRidge in different noises for Burgers equation ut=- uux+0.1uxx
| 噪声数据量 | NN-PDE | STRidge |
| 无 | ut=- 0.9988 uux+0.0999 uxx | ut=- 1.001 uux+0.102 uxx |
| 1% | ut=- 0.9965 uux+0.0997 uxx | ut=- 0.960 uux+0.102 uxx |
| 5% | ut=- 0.9992 uux+0.1003 uxx | ut=- 0.824 uux+0.117 uxx - 0.06 u2uxx |
| 10% | ut=- 0.9789 uux+0.0998 uxx | 无法得到简约的方程 |
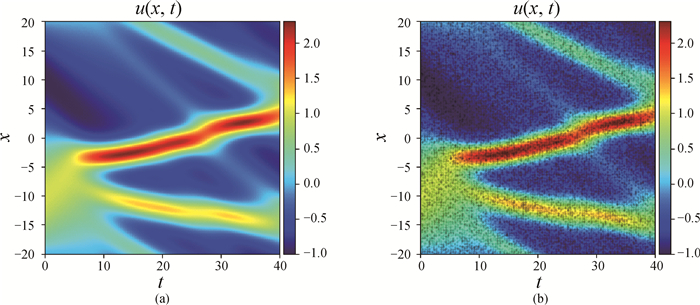
图4 (a) KdV方程解u的云图;(b) 图中一部分代表从数据中随机选择的25 000组 (背景代表解u的云图,黑点是选择的数据。)
Fig.4 (a) Solution of KdV equation in the form of heat map and (b) a portion of the map indicating 25 000 data selected randomly from the dataset (The background represents solution u in the dataset by heat map, and the black dots are selected data.)
| 噪声数据量 | NN-PDE | DL-PDE |
| 无 | ut=- 0.9995 uux - 0.9995 uxxx | ut=- 0.993 uux - 0.996 uxxx |
| 1% | ut=- 0.9986 uux - 0.9991 uxxx | ut=- 0.986 uux - 0.985 uxxx |
| 5% | ut=- 0.9995 uux - 0.9973 uxxx | ut=- 0.968 uux - 0.974 uxxx |
| 10% | ut=- 1.0018 uux - 1.0023 uxxx | ut=- 0.940 uux - 0.936 uxxx |
表2 KdV方程ut=- uux - uxxx在不同噪声中NN-PDE和DL-PDE的性能
Table 2 Performance of NN-PDE and STRidge in different noises for KdV equation ut=- uux - uxxx
| 噪声数据量 | NN-PDE | DL-PDE |
| 无 | ut=- 0.9995 uux - 0.9995 uxxx | ut=- 0.993 uux - 0.996 uxxx |
| 1% | ut=- 0.9986 uux - 0.9991 uxxx | ut=- 0.986 uux - 0.985 uxxx |
| 5% | ut=- 0.9995 uux - 0.9973 uxxx | ut=- 0.968 uux - 0.974 uxxx |
| 10% | ut=- 1.0018 uux - 1.0023 uxxx | ut=- 0.940 uux - 0.936 uxxx |
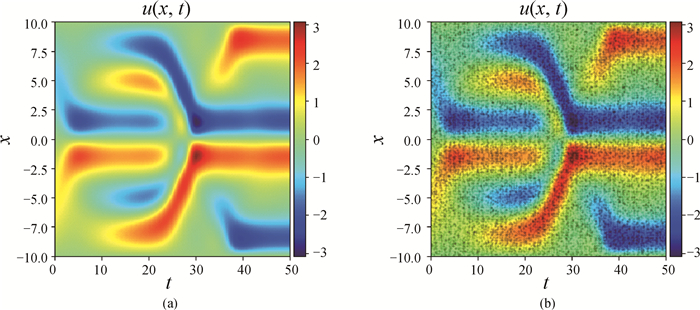
图5 (a) KS方程解u的云图;(b)图的一部分代表从数据中随机选择的25 000组 (背景代表解u的云图,黑点是选择的数据。)
Fig.5 (a) Solution of KS equation in the form of heat map and (b) a portion of the map indicating 25 000 data selected randomly from the dataset (The background represents the solution u in the dataset by heat map, and the black dots are selected data.)
| 噪声数据量 | 控制方程 |
| 无 | ut=- 0.9969 uux - 0.9966 uxx - 0.9972 uxxxx |
| 1% | ut=- 0.9982 uux - 0.9954 uxx - 0.9964 uxxxx |
| 5% | ut=- 0.9962 uux - 0.9946 uxx - 0.9955 uxxxx |
| 10% | ut=- 0.9780 uux - 1.0020 uxx - 0.9964 uxxxx |
表3 KS方程ut=- uux - uxx - uxxxx在不同噪声中NN-PDE的性能
Table 3 Performance of NN-PDE and STRidge in different noises for KS equation ut=- uux - uxx - uxxxx
| 噪声数据量 | 控制方程 |
| 无 | ut=- 0.9969 uux - 0.9966 uxx - 0.9972 uxxxx |
| 1% | ut=- 0.9982 uux - 0.9954 uxx - 0.9964 uxxxx |
| 5% | ut=- 0.9962 uux - 0.9946 uxx - 0.9955 uxxxx |
| 10% | ut=- 0.9780 uux - 1.0020 uxx - 0.9964 uxxxx |
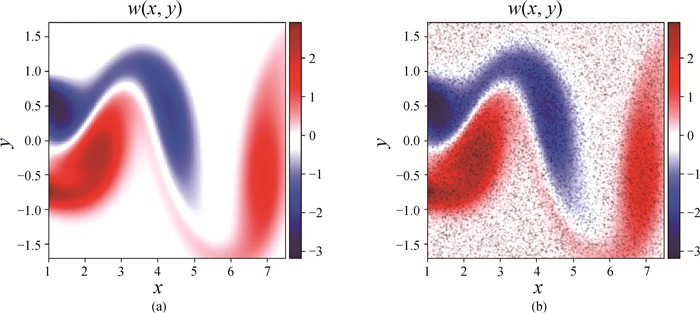
图6 (a) NS方程解w的云图;(b)图中一部分代表从数据中随机选择的50 000组 (背景代表解w的云图,黑点是选择的数据。)
Fig.6 (a) Solution of NS equation in the form of heat map and (b) a portion of the map indicating 50 000 data selected randomly from the dataset (The background represents the solution w in the dataset by heat map, and the black dots are selected data.)
| 噪声数据量 | 控制方程 |
| 无 | wt=- 0.9995 uwx- 0.9986 vwy+0.0100 wxx+0.0100 wyy |
| 1% | wt=- 0.9993 uwx- 0.9982 vwy+0.0100 wxx+0.0100 wyy |
| 5% | wt=- 0.9988 uwx- 0.9919 vwy+0.0100 wxx+0.0100 wyy |
| 10% | wt=- 0.9936 uwx- 0.9729 vwy+0.0095 wxx+0.0108 wyy |
表4 NS方程wt=- uwx - vwy+0.01(wxx+wyy) 在不同噪声中NN-PDE的性能
Table 4 Performance of NN-PDE and STRidge in different noises for NS equation wt=- uwx - vwy+0.01(wxx+wyy)
| 噪声数据量 | 控制方程 |
| 无 | wt=- 0.9995 uwx- 0.9986 vwy+0.0100 wxx+0.0100 wyy |
| 1% | wt=- 0.9993 uwx- 0.9982 vwy+0.0100 wxx+0.0100 wyy |
| 5% | wt=- 0.9988 uwx- 0.9919 vwy+0.0100 wxx+0.0100 wyy |
| 10% | wt=- 0.9936 uwx- 0.9729 vwy+0.0095 wxx+0.0108 wyy |
| 1 |
DOI |
| 2 |
DOI |
| 3 |
DOI |
| 4 |
DOI |
| 5 |
DOI |
| 6 |
DOI |
| 7 |
DOI |
| 8 |
DOI |
| 9 |
DOI |
| 10 |
DOI |
| 11 |
DOI |
| 12 |
|
| 13 |
DOI |
| 14 |
KNOWLES I, RENKA R J. Methods for numerical differentiation of noisy data[J]. Electronic Journal of Differential Equations, Conference 21(2014): 235-246.
|
| 15 |
DOI |
| 16 |
DOI |
| 17 |
DOI |
| 18 |
DOI |
| 19 |
|
| 20 |
|
| 21 |
DOI |
| 22 |
|
| 23 |
|
| [1] | 胡军, 刘全, 倪国喜. 时变偏微分方程的贝叶斯稀疏识别方法[J]. 计算物理, 2021, 38(1): 25-34. |
| [2] | 孔令海, 孔令波, 许海波, 贾清刚. 含Laplace-Gauss型混合噪声图像二阶正则化重建方法[J]. 计算物理, 2019, 36(3): 280-290. |
| [3] | 梅树立, 张森文, 陆启韶. 基于同伦技术的Burgers方程的小波精细积分算法[J]. 计算物理, 2007, 24(1): 54-58. |
| [4] | 梅树立, 陆启韶, 张森文. 求解非线性偏微分方程的自适应小波精细积分法[J]. 计算物理, 2004, 21(6): 523-530. |
| [5] | 李晓峰, 朱本仁. Radon变换在渗流力学反问题中的应用[J]. 计算物理, 2001, 18(2): 115-118. |
| [6] | 史金松, 庄卫华, 章卫军. Kaczmarz迭代与流场计算[J]. 计算物理, 1991, 8(3): 279-286. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||
版权所有 © 《计算物理》编辑部
地址:北京市海淀区丰豪东路2号 邮编:100094 E-mail:jswl@iapcm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发
