滚动轴承支撑下转子系统的耦合故障动力学

doi:10.19596/j.cnki.1001-246x.8503

摘要/Abstract

摘要：

研究含波纹度滚动轴承支撑下裂纹转子系统发生碰摩故障时的动力学特性。建立滚动轴承内外圈表面的波纹模型，采用综合模型描述转子轴系的呼吸型裂纹，研究转子系统与定子碰摩的非线性动力学特性。根据拉格朗日方程建立四自由度含波纹度滚动轴承支撑下裂纹-碰摩转子系统动力学方程，采用四阶Runge-Kutta方法进行数值求解，研究波纹度幅值、波纹数、轴承间隙及偏心量等参数对系统非线性特性的影响。结果表明：在低转速区间，随着波纹度最大幅值的增大，系统振动响应逐渐混乱，间谐波数量以及幅值随之增大，且逐渐出现连续特征谱。随着转速的逐渐增大且到达临界转速后横向位移随着轴承间隙的增大逐渐减小，随着偏心量的增大逐渐增大。到达超临界转速后，转子系统呈现出较强的非线性特征，横向位移随着最大幅值的增大而逐渐增大，振动响应随着偏心量的增大由混沌运动转变为周期1运动和拟周期运动。大轴承间隙下，系统在低转速区随着轴承间隙的增大而趋于稳定，在超高转速区则一直处于混沌运动中。波纹数与滚珠个数一致的系统相比不一致的系统在低转速区更加稳定，超临界转速区更加混乱。

关键词: 波纹度滚动轴承, 转子, 非线性动力学, 裂纹, 碰摩

Abstract:

Dynamic characteristics of a cracked rotor system supported by corrugated rolling bearing is studied. A ripple model of inner and outer ring surface of rolling bearing is established, in which the respiratory crack of rotor shaft system is described with a comprehensive model. The nonlinear dynamic characteristics of rub impact between rotor system and stator is studied. With Lagrange equation, dynamic equation of crack rub impact rotor system supported by four degree of freedom rolling bearing with waviness is established. A fourth-order Runge Kutta method is used to solve the equation numerically. Effects of parameters such as waviness amplitude, waviness number, bearing clearance and eccentricity on nonlinear characteristics of the system are studied. It shows that in low speed range, with the increase of the maximum amplitude of waviness, the vibration response of the system is gradually chaotic, the number and amplitude of interharmonics increase, and the continuous characteristic spectrum appears gradually. The lateral displacement decreases with the increase of bearing clearance and increases with the increase of eccentricity after reaching a critical speed. After reaching the supercritical speed, the rotor system presents strong nonlinear characteristics. The lateral displacement increases gradually with the increase of the maximum amplitude, and the vibration response changes from chaotic motion to periodic 1 motion and quasi periodic motion with the increase of eccentricity. Under the condition of large bearing clearance, the system tends to be stable with the increase of bearing clearance in a low speed region, while it is in chaotic motion in the ultra-high speed region. Compared with a system with same number of corrugations and balls, a inconsistent system is more stable in the low speed region and more chaotic in the supercritical speed region.

Key words: waviness rolling bearing, rotor, nonlinear dynamics, crackle, rubbing

余登亮, 南国防, 姜珊, 宋传冲. 滚动轴承支撑下转子系统的耦合故障动力学[J]. 计算物理, 2022, 39(6): 733-743.

Dengliang YU, Guofang NAN, Shan JIANG, Chuanchong SONG. Coupling Fault Dynamics of Rotor System Supported by Rolling Bearing[J]. Chinese Journal of Computational Physics, 2022, 39(6): 733-743.

图/表 16

图1 含内外波纹故障的滚动轴承示意图

Fig.1 A schematic of rolling bearing with internal and external ripple fault

图2 碰摩力模型示意图

Fig.2 A schematic of rub impact force model

图3 裂纹轴横截面示意图

Fig.3 A cross section of crack shaft

图4 耦合故障转子系统示意图

Fig.4 A schematic of coupling fault rotor system

表1 系统主要参数

Table 1 Main parameters of the system

参数	值
轴承处集中质量m₁/kg	4
轮盘处集中质量m₂/kg	32.1
无裂纹转轴刚度k/(N·m^-1)	2.5 × 10⁷
轴承阻尼c₁/(N·m·s^-1)	1 050
圆盘阻尼c₂/(N·m·s^-1)	2 100
摩擦系数f	0.1
定子径向刚度k_r/(N·m^-1)	3.5 × 10⁷
转定子间隙δ/m	2 × 10^-5
偏心量e/m	1 × 10^-5
最大幅值A/m	1 × 10^-6
波纹数N_w	8

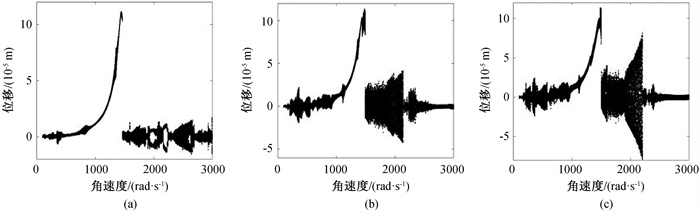
图5 不同最大幅值下系统振动响应分岔图(a) A=1 × 10-6 m; (b) A=3 × 10-6 m; (c) A=4 × 10-6 m

Fig.5 Bifurcation diagrams of system vibration response under different maximum amplitudes (a) A=1 × 10-6 m; (b) A=3 × 10-6 m; (c) A=4 × 10-6 m

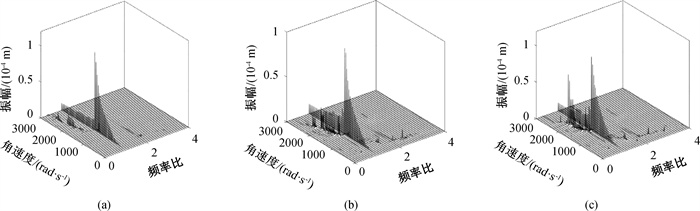
图6 不同最大幅值下系统振动响应频谱瀑布图(a) A=1 × 10-6 m; (b) A=3 × 10-6 m; (c) A=4 × 10-6 m

Fig.6 Spectrum waterfalls of system vibration response under different maximum amplitudes (a) A=1 × 10-6 m; (b) A=3 × 10-6 m; (c) A=4 × 10-6 m

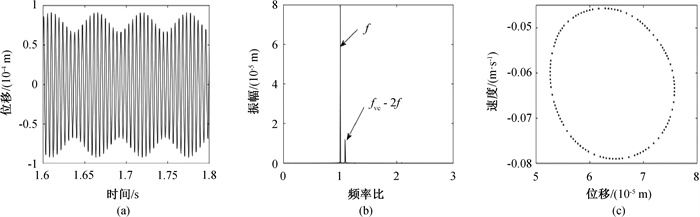
图7 ω = 1350 rad ·s-1、A = 1 × 10-6 m时耦合故障系统(a) 时间历程、(b) 频谱及(c) Poincaré截面

Fig.7 (a) Time history, (b) spectrum and (c) Poincaré section of coupled fault system at ω = 1350 rad ·s-1, A = 1 × 10-6 m

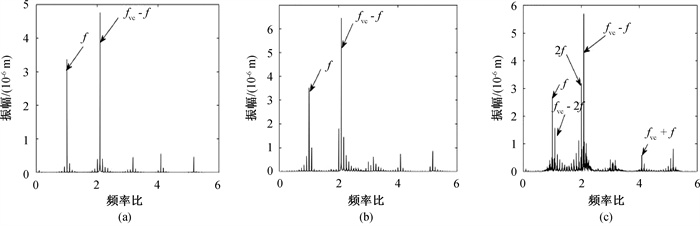
图8 ω = 350 rad ·s-1时不同最大幅值的耦合故障转子系统频谱(a) A = 1 × 10-6 m; (b) A = 3 × 10-6 m; (c) A = 4 × 10-6 m

Fig.8 Spectrum diagrams of a coupled fault rotor system with different maximum amplitudes at ω = 350 rad ·s-1 (a) A = 1 × 10-6 m; (b) A = 3 × 10-6 m; (c) A = 4 × 10-6 m

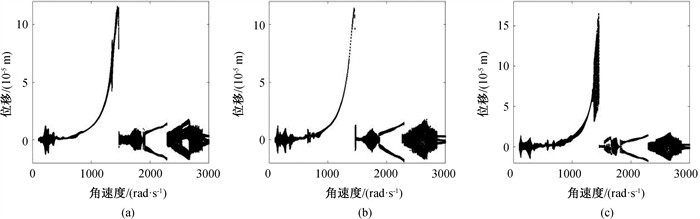
图9 不同波纹数下系统振动响应分岔图(a) Nw = 7; (b) Nw = 9; (c) Nw = 10

Fig.9 Bifurcation diagrams of system vibration response under ripple numbers (a) Nw = 7; (b) Nw = 9; (c) Nw = 10

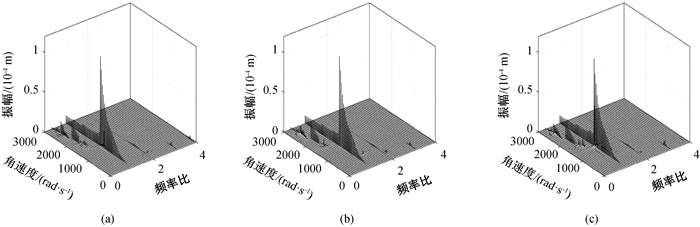
图10 不同波纹数下系统振动响应频谱瀑布图(a) Nw = 7; (b) Nw = 9; (c) Nw = 10

Fig.10 Waterfalls of system vibration response spectrum under ripple numbers (a) Nw = 7; (b) Nw = 9; (c) Nw = 10

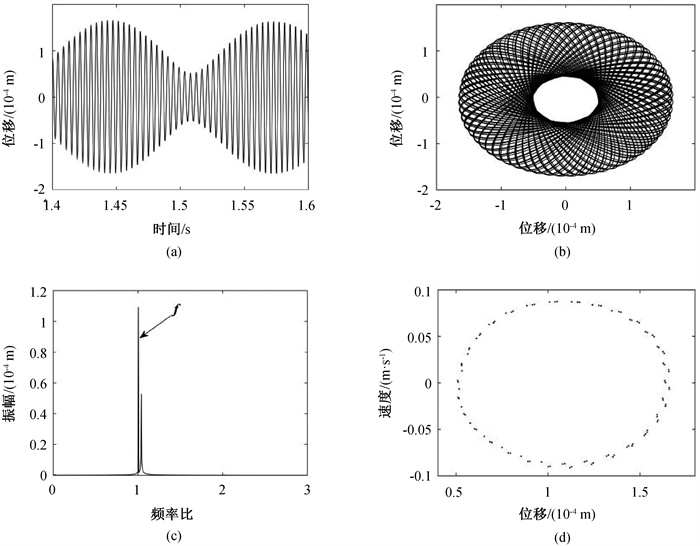
图11 ω = 1450 rad ·s-1、Nw = 10时耦合故障转子系统(a) 时间历程、(b) 轴心轨迹、(c) 频谱和(d) Poincaré截面

Fig.11 Time history, (b) axis trajectory, (c) spectrum and (d) Poincaré section diagram of coupled fault rotor system at ω = 1 450 rad ·s-1 and Nw = 10

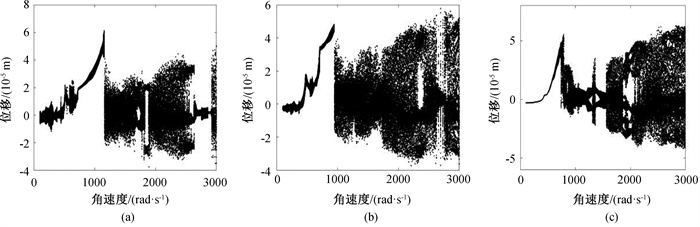
图12 不同轴承间隙下系统振动响应分岔图(a) r = 20 × 10-6 m; (b) r = 30 × 10-6 m; (c) r = 40 × 10-6 m

Fig.12 Bifurcation diagrams of system vibration response under different bearing clearance (a) r = 20 × 10-6 m; (b) r = 30 × 10-6 m; (c) r = 40 × 10-6 m

图13 不同轴承间隙下系统振动响应频谱瀑布图(a) r = 20 × 10-6 m; (b) r = 30 × 10-6 m; (c) r = 40 × 10-6 m

Fig.13 Spectrum waterfalls of system vibration response under different bearing clearances (a) r = 20 × 10-6 m; (b) r = 30 × 10-6 m; (c) r = 40 × 10-6 m

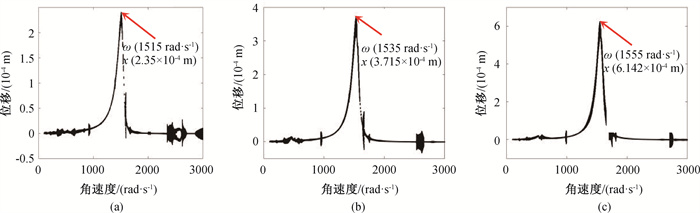
图14 不同偏心量时的系统振动响应分岔图(a) e = 2 × 10-5 m; (b) e = 3 × 10-5 m; (c) e = 5 × 10-5 m

Fig.14 Bifurcation diagrams of system vibration response under different eccentricity (a) e = 2 × 10-5 m; (b) e = 3 × 10-5 m; (c) e = 5 × 10-5 m

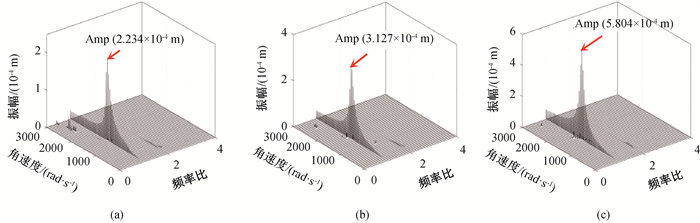
图15 不同偏心量时的系统振动响应频谱瀑布图(a) e = 2 × 10-5 m; (b) e = 3 × 10-5 m; (c) e = 5 × 10-5 m

Fig.15 Spectrum waterfalls of system vibration response under different eccentricity (a) e = 2 × 10-5 m; (b) e = 3 × 10-5 m; (c) e = 5 × 10-5 m

参考文献 32

1	康锋, 张耀强, 杨茹萍, 等. 考虑波纹度的薄壁轴承-转子系统非线性强迫振动分析[J]. 振动与冲击, 2017, 36 (1): 96- 101.
2	顾晓辉, 杨绍普, 刘永强, 等. 表面波纹度对滚动轴承-转子系统非线性振动的影响[J]. 振动与冲击, 2014, 33 (8): 109- 114.
3	张耀强, 陈建军, 邓四二, 等. 考虑表面波纹度的滚动轴承-转子系统非线性动力特性[J]. 航空动力学报, 2008, 19 (9): 1731- 736. DOI
4	KANKAR P K, SHARMA S C, HARSHA S P. Dynamic response of an unbalanced rotor supported on bearing with outer race waviness[C]. Asme International Design Engineering Technical Conferences & Computers & Information in Engineering Conference, 2013.
5	HAN Q S , YANG D Q . Method of Green's founctions applied to lubrication theory[J]. Chinese Journal of Computational Physics, 1986, 3 (4): 467- 472.
6	邹剑, 董广明, 陈进. 含初始弯曲裂纹转子的振动分析[J]. 振动与冲击, 2012, 31 (3): 153- 156. DOI
7	何成兵, 顾煜炯, 宋光雄. 裂纹转子弯扭耦合振动非线性特性分析[J]. 振动与冲击, 2012, 31 (9): 33- 38.
8	向玲, 高雪媛. 考虑非线性油膜力的裂纹转子动力学特性仿真[J]. 动力工程学报, 2017, 37 (6): 454- 460. DOI
9	翟鹏程. 横向裂纹转子的非线性振动特性及其稳定性研究[D]. 北京: 华北电力大学(北京), 2017.
10	林言丽. 斜裂纹转子系统的动力学特性[D]. 北京: 清华大学, 2009.
11	杨丹. 含裂纹转子系统刚度及动力学特性研究[D]. 杭州: 浙江大学, 2012.
12	刘长利, 谢朋儒, 周邵萍, 等. 基于有限元的呼吸裂纹转子动力学特性[J]. 振动、测试与诊断, 2011, 31 (2): 185- 189. 185-189+265
13	LIONG R T , PROPPE C . Finite element multibody simulation of a breathing crack in a rotor with a cohesive zone model[J]. ISRN Mechanical Engineering, 2014, 2013, 1- 10.
14	LIONG R T , PROPPE C . Implementation of a cohesive zone model for the investigation of the dynamic behavior of a rotating shaft with a transverse crack[J]. PAMM, 2010, 10 (1): 125- 126.
15	钱征文, 程礼, 张海威, 等. 基于涡动角的裂纹转子模型稳定性分析[J]. 汽轮机技术, 2009, 51 (3): 175- 179.
16	刘政, 王建军. 呼吸性裂纹转子的瞬态振动特性分析[J]. 振动与冲击, 2016, 35 (7): 233- 240.
17	张亚辉, 赵军. 含裂纹故障的转子-轴承系统的非线性特性分析[J]. 舰船电子工程, 2016, 36 (8): 193- 197.
18	蒯腾飞, 赵昌方, 夏文嘉, 等. 含裂纹转子系统动力学建模与实验研究[J]. 科学技术与工程, 2019, 19 (8): 58- 65.
19	于海, 陈予恕, 曹庆杰. 多自由度裂纹转子系统非线性动力学特性分析[J]. 振动与冲击, 2014, 33 (7): 92- 98.
20	路振勇. 航空发动机高压转子-空心轴裂纹系统动力学特性分析[D]. 哈尔滨: 哈尔滨工业大学, 2013.
21	路振勇, 陈予恕, 侯磊, 等. 常开空心轴裂纹转子系统的动力学特性[J]. 航空动力学报, 2015, 30 (2): 422- 430.
22	REN Z H , ZHAO S H , LI C F , et al. Dynamic characteristics of multi-degrees of freedom system rotor-bearing system with coupling faults of rub-impact and crack[J]. Chinese Journal of Mechanical Engineering, 2014, 27 (4): 785- 792.
23	LI H G , LI M , LI C , et al. Multi-faults decoupling on turbo-expander using differential-based ensemble empirical mode decomposition[J]. Mechanical Systems & Signal Processing, 2017, 93 (1): 267- 280.
24	VASHISHT R K, PENG Q J. Dynamic modelling and diagnosis of transverse crack and rotor/stator rub in a flexible rotor system[C]. ASME 2019 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 2019.
25	罗跃纲, 张松鹤, 闻邦椿. 转子-轴承系统裂纹-碰摩耦合故障的非线性特性研究[J]. 振动与冲击, 2005, 24 (3): 43- 133. 43-46, 132-133
26	刘颖慧. 转子裂纹及碰摩故障的混沌分形特征研究[D]. 大庆: 大庆石油学院, 2009.
27	曲秀秀, 陈果, 乔保栋. 裂纹-碰摩耦合故障动力学建模及实验分析[J]. 机械科学与技术, 2012, 31 (2): 310- 316.
28	艾延廷, 付琪, 田晶, 等. 基于融合信息熵距的转子裂纹-碰摩耦合故障诊断方法[J]. 航空动力学报, 2013, 28 (10): 2161- 2166.
29	CHANG-JIAN C W , WANG C C , CHU L M . Bifurcation and chaos analysis of gear pair system based on crack rotor-bearing system with rub-impact effect[J]. MATEC Web of Conferences, 2018, 201, 01008.
30	YANG Z A , BIAN Y Y . Primary resonance of strong nonlinear torsional vibration system of diesel shafting[J]. Chinese Journal of Computational Physics, 2017, 34 (3): 374- 378.
31	JI Z Z , WANG B . A semi-Lagrangian integration scheme keeping conservation of total energy[J]. Chinese Journal of Computational Physics, 1996, 13 (4): 403- 409.
32	高建民, 朱晓梅. 转轴上裂纹开闭模型的研究[J]. 应用力学学报, 1992, 9 (1): 108- 112.

[1]	李建伟, 项璇, 王景栋, 胡石, 陈铮, 贺元骅. 不同温度和扰动应变作用下纳米微裂纹的晶体相场研究[J]. 计算物理, 2022, 39(6): 717-726.
[2]	郭怀民, 赵国忠, 姜丽娟. 磁电弹性体中螺型位错与唇口裂纹的相互作用[J]. 计算物理, 2022, 39(1): 33-40.
[3]	郭怀民, 赵国忠. 磁电弹性体中多条位错与Griffith裂纹[J]. 计算物理, 2020, 37(2): 198-204.
[4]	高英俊, 杨瑞琳, 黄礼琳, 刘瑶. 纳观尺度裂纹扩展微观机理的晶体相场法研究[J]. 计算物理, 2017, 34(4): 453-460.
[5]	葛仁余, 牛忠荣, 程长征, 胡宗军, 薛伟伟. 边界元法分析二维线弹性裂纹扩展[J]. 计算物理, 2015, 32(3): 310-320.
[6]	高英俊, 罗志荣, 邓芊芊, 黄礼琳, 林葵. 韧性材料的微裂纹扩展与分叉的晶体相场模拟[J]. 计算物理, 2014, 31(4): 471-478.
[7]	段耀勇, 陈荣华, 盛剑霓, 陈雨生. 涡流检测中的微扰模型[J]. 计算物理, 1997, 14(S1): 963-695.