波动方程的高精度数值解方法

doi:10.19596/j.cnki.1001-246x.8732

摘要/Abstract

摘要：

本文提出重心Lagrange插值配点法求解(2+1)维波动方程和(3+1)维波动方程。介绍了重心Lagrange插值法并且给出配点法的矩阵格式。波动方程的解函数和初边值条件均用Lagrange插值近似，利用配点法得到离散方程，获得波动方程的矩阵表达式。分别用附加法和置换法施加波动方程的初边值条件。数值算例表明：重心Lagrange插值配点法求解波动方程具有较高的计算精度和计算效率。

关键词: 重心Lagrange插值, 波动方程, 配点法, 矩阵格式

Abstract:

A barycentric Lagrange interpolation collocation method is proposed to solve the three-dimensional and four-dimensional wave equations. Firstly, the barycentric Lagrange interpolation method is introduced and the matrix format of the collocation method is given. Secondly, the solution function and initial boundary conditions of the wave equation are approximated by Lagrange interpolation. The discrete equation is obtained by collocation method, and the matrix expression of the wave equation is obtained. Finally, the initial and boundary conditions of the wave equation are imposed by the addition method and the replacement method respectively. Numerical examples show that the barycentric Lagrange interpolation collocation method has high computational accuracy and efficiency.

Key words: barycentric Lagrange interpolation, wave equation, collocation method, matrix scheme

中图分类号:

O469

袁洪旺, 王希胤, 李金. 波动方程的高精度数值解方法[J]. 计算物理, 2024, 41(4): 426-439.

Hongwang YUAN, Xiyin WANG, Jin LI. High Accuracy Numerical Solution of Wave Equation[J]. Chinese Journal of Computational Physics, 2024, 41(4): 426-439.

图/表 13

表1 不同节点数边界条件施加方法为附加法与置换法的绝对误差、相对误差和收敛阶

Table 1 Absolute error, relative error and the order of convergence of additional method and displacement method

节点数m=n=h	附加法			置换法
节点数m=n=h	E_a	rate	E_r	E_a	rate	E_r
9	9.704 1×10^-3		1.450 6×10^-3	9.801 2×10^-3		1.465 1×10^-3
11	1.021 9×10^-4	6.56	1.141 1×10^-5	2.373 0×10^-4	5.37	2.649 9×10^-5
13	9.277 3×10^-7	6.78	8.116 6×10^-8	3.526 0×10^-6	6.07	3.084 9×10^-7
15	8.489 6×10^-9	6.77	6.021 9×10^-10	3.623 9×10^-8	6.60	2.570 5×10^-9
17	5.010 3×10^-11	7.40	2.956 7×10^-12	1.781 3×10^-8	1.02	1.051 2×10^-9
19	3.873 4×10^-11	0.37	1.940 3×10^-12	2.787 4×10^-8	-0.6	1.396 3×10^-9

表2 三点中心差分法在t=1时刻的绝对误差、相对误差和收敛阶

Table 2 Absolute error, relative error and the order of convergence of three center difference method at t=1

节点数m=n=$\sqrt{h}$	三点中心差分法
节点数m=n=$\sqrt{h}$	E_a	rate	E_r
4	2.087 7×10^-2		1.443 9×10^-2
9	5.098 7×10^-3	2.03	1.322 4×10^-3
18	2.541 7×10^-3	1.00	3.102 2×10^-4
36	1.270 9×10^-3	1.00	7.534 0×10^-5
64	7.118 6×10^-4	0.84	2.344 5×10^-5

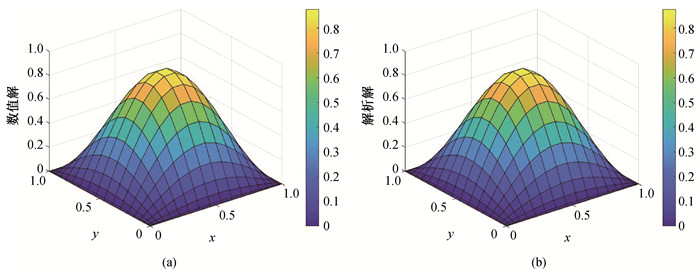
图1 当m = n = h = 19，边界条件施加方法为附加法，h = 10时的(a)数值解和(b)解析解

Fig.1 (a)Numerical solution and (b) analytical solution of additional method at h = 10 with m = n = h = 19

图2 当m = n = h = 19，边界条件施加方法为附加法，h = 10的误差

Fig.2 Domain error of additional method at h = 10 with m = n = h = 19

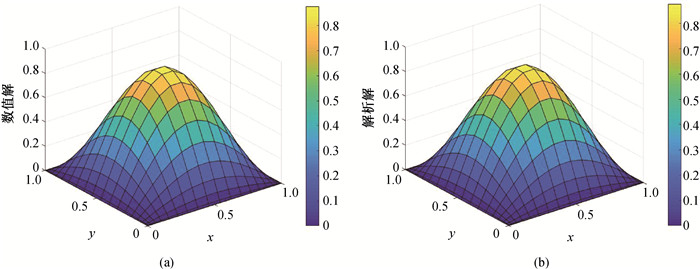
图3 当m = n = h = 19，边界条件施加方法为置换法，h = 10的(a)数值解和(b)解析解

Fig.3 (a)Numerical solution and (b) analytical solution of displacement method at h=10 with m = n = h = 19

图4 当m = n = h = 19，边界条件施加方法为置换法，h = 10的误差

Fig.4 Domain error of displacement method at h = 10 with m = n = h = 19

表3 不同节点数边界条件施加方法为附加法与置换法的绝对误差、相对误差和收敛阶

Table 3 Absolute error, relative error and the order of convergence of additional method and displacement method

节点数m=n=h	附加法			置换法
节点数m=n=h	E_a	rate	E_r	E_a	rate	E_r
9	6.718 7×10^-4		2.157 3×10^-5	7.267 6×10^-4		2.333 6×10^-5
11	3.321 9×10^-6	7.66	8.174 0×10^-8	8.275 7×10^-6	6.46	2.036 4×10^-7
13	1.856 5×10^-8	7.48	3.644 2×10^-10	6.241 0×10^-8	7.05	1.225 1×10^-9
15	1.077 7×10^-10	7.43	1.738 3×10^-12	4.258 6×10^-8	0.55	6.868 9×10^-10
17	1.227 3×10^-10	-0.2	1.664 1×10^-12	1.977 4×10^-7	-2.2	2.681 2×10^-9
19	3.116 7×10^-10	-1.3	3.616 9×10^-12	1.413 5×10^-7	0.50	1.640 4×10^-9

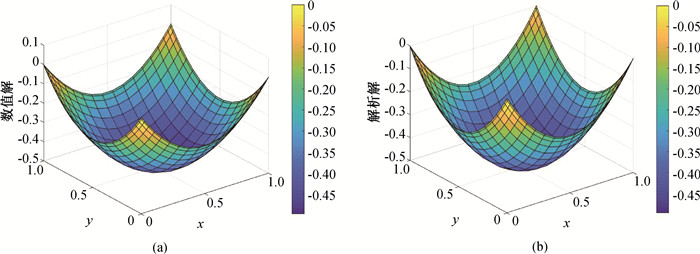
图5 当m = n = h = 19，边界条件施加方法为附加法，h = 1的(a)数值解和(b)解析解

Fig.5 (a)Numerical solution and (b) analytical solution of additional method at h = 1 with m = n = h = 19

图6 当m = n = h = 19，边界条件施加方法为附加法，h = 1时的误差

Fig.6 Domain error at h = 1 with additional method and m = n = h = 19

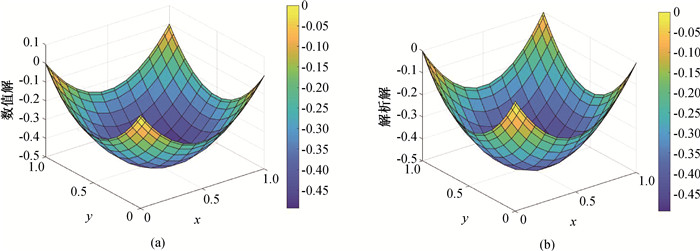
图7 当m = n = h = 15，边界条件施加方法为置换法，h = 1的(a)数值解和(b)解析解

Fig.7 (a) Numerical solution and (b) analytical solution of displacement method at h = 1 with m = n = h = 15

图8 当m = n = h = 15，边界条件施加方法为置换法，h = 1时刻的误差

Fig.8 Domain error of displacement method at h = 1 with m = n = h = 15

表4 不同节点数边界条件施加方法为附加法与置换法的绝对误差、相对误差和收敛阶

Table 4 Absolute error, relative error and the order of convergence with additional method and displacement method

节点数m=n=s=h	附加法			置换法
节点数m=n=s=h	E_a	rate	E_r	E_a	rate	E_r
7	5.578 9×10^-1		7.490 9×10^-2	5.069 6×10^-2		6.807 1×10^-3
9	5.774 6×10^-2	3.27	4.728 8×10^-3	2.031 4×10^-2	1.32	1.663 5×10^-3
11	1.259 3×10^-3	5.52	6.939 6×10^-5	1.143 6×10^-3	4.15	6.302 0×10^-5
13	2.137 9×10^-5	5.88	8.465 9×10^-7	3.270 5×10^-5	5.13	1.295 1×10^-6
15	2.961 0×10^-7	6.17	8.830 6×10^-9	5.837 7×10^-7	5.81	1.741 0×10^-8
17	2.488 4×10^-9	6.89	5.789 9×10^-11	7.225 8×10^-9	6.34	1.681 2×10^-10

表5 三点中心差分法在t=1时刻的绝对误差、相对误差和收敛阶

Table 5 Time absolute error, relative error and the order of convergence with three center difference method at t=1

节点数m=n=s=$\sqrt{h}$	三点中心差分法
节点数m=n=s=$\sqrt{h}$	E_a	rate	E_r
4	3.349 9×10^-1		2.441 2×10^-1
9	2.202 1×10^-1	0.61	3.690 7×10^-2
17	1.579 5×10^-1	0.48	9.359 0×10^-3
31	1.158 1×10^-1	0.45	2.672 8×10^-3
62	8.132 4×10^-2	0.51	6.473 3×10^-4

参考文献 26

1	汪勇, 穆鹏飞, 蔡文杰, 等. 五对角紧致差分格式优化及二维声波传播波动方程数值模拟[J]. 石油物探, 2019, 58 (4): 486- 498. DOI
2	BIAZAR J , ESLAMI M . A new technique for non-linear two-dimensional wave equations[J]. Scientia Iranica, 2013, 20 (2): 359- 363.
3	FU Zuntao , LIU Shikuo , LIU Shida , et al. New jacobi elliptic function expansion and new periodic solutions of nonlinear wave equations[J]. Physics Letters A, 2001, 290 (1/2): 72- 76.
4	马友能, 余锦华, 汪源源. 二阶声场波动方程的非分裂完全匹配层算法[J]. 声学学报, 2013, 38 (6): 681- 686.
5	王兆清, 徐子康. 基于平面问题的位移压力混合配点法[J]. 计算物理, 2018, 35 (1): 77- 86.
6	HAMILTON B , BILBAO S . Optimised 25-point finite difference schemes for the three-dimensional wave equation[J]. Proceedings of Meetings on Acoustics, 2017, 28 (1): 015022.
7	马德堂, 朱光明. 有限元法与伪谱法混合求解弹性波动方程[J]. 地球科学与环境学报, 2004, (1): 61- 64.
8	张荣培, 王迪, 蔚喜军, 等. 基于广义交替数值通量的局部间断Galerkin方法求解二维波动方程[J]. 物理学报, 2020, 69 (2): 60- 66.
9	ZHANG Zan , LI Dongming , CHENG Yumin , et al. The improved element-free Galerkin method for three-dimensional wave equation[J]. Acta Mechanica Sinica, 2012, 28 (3): 808- 818. DOI
10	李坤, 黄其柏, 林立广. 二阶时域波动方程的无网格方法求解[J]. 华中科技大学学报(自然科学版), 2011, 39 (3): 26- 29.
11	CASULLI V . Semi-implicit finite difference methods for the two-dimensional shallow water equations[J]. Journal of Computational Physics, 1990, 86 (1): 56- 74.
12	CASULLI V , CHENG R T . Semi-implicit finite difference methods for three-dimensional shallow water flow[J]. International Journal for Numerical Methods in Fluids, 1992, 15 (6): 629- 648.
13	DEHGHAN M , MOHEBBI A . The combination of collocation, finite difference, and multigrid methods for solution of the two-dimensional wave equation[J]. Numerical Methods for Partial Differential Equations, 2008, 24 (3): 897- 910.
14	WEI Hui , JI Shuguan . Periodic solutions of a semilinear variable coefficient wave equation under asymptotic nonresonance conditions[J]. Science China Mathematics, 2023, 66 (1): 79- 90.
15	DEHGHAN M , SHOKRI A . A meshless method for numerical solution of the one-dimensional wave equation with an integral condition using radial basis functions[J]. Numerical Algorithms, 2009, 52 (3): 461- 477.
16	蒋长锦. 波动方程辛算法的迭代求解[J]. 计算物理, 2002, 19 (1): 13- 16.
17	张文飞, 李晓江. 双参数波动方程反问题的数值解法[J]. 计算物理, 1997, (2): 2- 8.
18	张大力, 刘家琦, 吴建成. 一维波动方程反问题求解的正则迭代法[J]. 计算物理, 2000, 17 (3): 326- 330.
19	马燕, 王兆清, 唐炳涛. 波动问题的高精度重心有理插值配点法[J]. 山东科学, 2012, 25 (3): 80- 87.
20	王兆清, 纪思源, 徐子康, 等. 不规则区域平面弹性问题的正则区域重心插值配点法[J]. 计算力学学报, 2018, 35 (2): 195- 201.
21	TAYLOR W J . Method of lagrangian curvilinear interpolation[J]. Journal of Research of the National Bureau of Standards, 1945, 35, 151- 155.
22	BERRUT J P , TREFETHEN L N . Barycentric lagrange interpolation[J]. SIAM Review, 2004, 46 (3): 501- 517.
23	LIU Hongyan , HUANG Jin , PAN Yubin , et al. Barycentric interpolation collocation methods for solving linear and nonlinear high-dimensional Fredholm integral equations[J]. Journal of Computational and Applied Mathematics, 2018, 327, 141- 154.
24	LI Jin , CHENG Yongling . Linear barycentric rational collocation method for solving heat conduction equation[J]. Numerical Methods for Partial Differential Equations, 2021, 37 (1): 533- 545.
25	LI Jin , SANG Yu . Linear barycentric rational collocation method for beam force vibration equation[J]. Shock and Vibration, 2021, 2021, 5584274.
26	LI Jin , SU Xiaoning , QU Jinzheng . Linear barycentric rational collocation method for solving telegraph equation[J]. Mathematical Methods in the Applied Sciences, 2021, 44 (14): 11720- 11737.

[1]	王兆清, 钱航, 李金. 移动边界问题的时空域正则区域迭代配点法[J]. 计算物理, 2021, 38(1): 16-24.
[2]	王磊磊, 纪乐, 马文涛. FGMs稳态热传导分析的重心Lagrange插值配点法[J]. 计算物理, 2020, 37(2): 173-181.
[3]	王兆清, 徐子康. 基于平面问题的位移压力混合配点法[J]. 计算物理, 2018, 35(1): 77-86.
[4]	刘婷, 马文涛. 重心Lagrange插值配点法求解二维双曲电报方程[J]. 计算物理, 2016, 33(3): 341-348.
[5]	陈可洋. 基于行波分离和角度域衰减的地震波叠前逆时成像条件[J]. 计算物理, 2016, 33(2): 205-211.
[6]	王兆清, 綦甲帅, 唐炳涛. 奇异源项问题的重心插值数值解[J]. 计算物理, 2011, 28(6): 883-888.
[7]	陈生昌, 马在田, WU Ru-Shan. 地震波传播路径追踪的波动方程方法[J]. 计算物理, 2008, 25(2): 186-190.
[8]	陈生昌, 马在田, WU Ru-Shan. 波动方程角度域偏移成像[J]. 计算物理, 2007, 24(2): 211-216.
[9]	陈生昌, 马在田, WU Ru-shan. 波动方程深度偏移的局部裂步Fourier传播算子[J]. 计算物理, 2006, 23(5): 604-608.
[10]	付汉清, 王泰春. 非稳腔傍轴波动方程高斯球面波修正方法的数值研究[J]. 计算物理, 2001, 18(6): 501-506.
[11]	杜其奎, 余德浩. 波动方程基于自然边界归化的区域分解算法[J]. 计算物理, 2001, 18(5): 417-422.
[12]	张大力, 吴建成, 刘家琦. 一维波动方程反问题求解的正则迭代法[J]. 计算物理, 2000, 17(3): 326-330.
[13]	郝现军, 朱本仁, 张关泉. 一维声波方程声阻抗反演问题的稳定性分析[J]. 计算物理, 1998, 15(5): 559-567.
[14]	张中明, 熊烨. BN、BH分子辐射带系的Franck-Condon因子计算[J]. 计算物理, 1998, 15(3): 343-348.
[15]	张文飞, 李晓江. 双参数波动方程反问题的数值解法[J]. 计算物理, 1997, 14(2): 129-130.