计算物理 ›› 2024, Vol. 41 ›› Issue (4): 418-425.DOI: 10.19596/j.cnki.1001-246x.8731
收稿日期:2023-03-20
出版日期:2024-07-25
发布日期:2024-08-24
通讯作者:
尚月强
作者简介:王雅莉,女,硕士研究生,研究方向为偏微分方程数值解与计算流体力学,E-mail:yali999ppbt@163.com
基金资助:
Yali WANG( ), Bo ZHENG, Yueqiang SHANG(
), Bo ZHENG, Yueqiang SHANG( )
)
Received:2023-03-20
Online:2024-07-25
Published:2024-08-24
Contact:
Yueqiang SHANG
摘要:
使用标准的混合有限元方法数值求解定常不可压Navier-Stokes方程所得速度解的精度常常受压力的影响。为了克服或减弱压力对速度精度的影响,本文将grad-div稳定化方法和两水平有限元方法相结合,提出数值求解定常不可压Navier-Stokes方程的两水平grad-div稳定化有限元方法。首先在粗网格上求解grad-div稳定化的非线性Navier-Stokes问题,然后在细网格上分别求解grad-div稳定化的Stokes型、Newton型和Oseen型的线性问题。最后给出数值算例验证两水平grad-div稳定化有限元方法的高效性。
中图分类号:
王雅莉, 郑波, 尚月强. 定常不可压Navier-Stokes方程的两水平grad-div稳定化有限元方法[J]. 计算物理, 2024, 41(4): 418-425.
Yali WANG, Bo ZHENG, Yueqiang SHANG. Two-level Grad-div Stabilized Finite Element Methods for Steady Incompressible Navier-Stokes Equations[J]. Chinese Journal of Computational Physics, 2024, 41(4): 418-425.
| 算法 | 1/h | 1/H | CPU/s | ‖▽(u-uh)‖0 | ‖p-ph‖0 | 速度收敛阶 | 压力收敛阶 |
| 单水平算法 | 8 | 0.077 | 1.364 7×10-1 | 2.468 2×10-2 | |||
| 27 | 0.715 | 3.977 0×10-3 | 2.031 3×10-3 | 2.906 64 | 2.053 12 | ||
| 64 | 3.071 | 3.025 5×10-4 | 3.596 1×10-4 | 2.984 79 | 2.006 16 | ||
| 125 | 14.536 | 4.071 3×10-5 | 9.419 0×10-5 | 2.996 16 | 2.001 27 | ||
| 标准算法 | 8 | 4 | 0.181 | 9.069 4×10-1 | 2.497 8×10-2 | ||
| 27 | 9 | 0.305 | 2.424 1×10-2 | 2.031 3×10-3 | 2.977 67 | 2.062 92 | |
| 64 | 16 | 1.65 | 1.832 2×10-3 | 3.596 1×10-4 | 2.992 35 | 2.006 15 | |
| 125 | 25 | 7.258 | 2.465 5×10-4 | 9.419 0×10-5 | 2.996 12 | 2.001 27 | |
| 算法1 | 8 | 4 | 0.063 | 1.521 3×10-1 | 2.471 8×10-2 | ||
| 27 | 9 | 0.296 | 3.978 5×10-3 | 2.031 3×10-3 | 2.995 61 | 2.054 31 | |
| 64 | 16 | 1.664 | 3.025 6×10-4 | 3.596 1×10-4 | 2.985 23 | 2.006 16 | |
| 125 | 25 | 7.494 | 4.071 3×10-5 | 9.419 0×10-5 | 2.996 17 | 2.001 27 | |
| 算法2 | 8 | 4 | 0.065 | 1.510 8×10-1 | 2.471 4×10-2 | ||
| 27 | 9 | 0.319 | 3.978 1×10-3 | 2.031 3×10-3 | 2.989 99 | 2.05417 | |
| 64 | 16 | 1.811 | 3.025 6×10-4 | 3.596 1×10-4 | 2.985 13 | 2.00616 | |
| 125 | 25 | 8.058 | 4.071 3×10-5 | 9.419 0×10-5 | 2.996 17 | 2.00127 | |
| 算法3 | 8 | 4 | 0.062 | 1.364 4×10-1 | 2.468 3×10-2 | ||
| 27 | 9 | 0.29 | 3.977 0×10-3 | 2.031 3×10-3 | 2.906 42 | 2.053 15 | |
| 64 | 16 | 1.62 | 3.025 5×10-4 | 3.596 1×10-4 | 2.984 79 | 2.006 16 | |
| 125 | 25 | 7.275 | 4.071 3×10-5 | 9.419 0×10-5 | 2.996 16 | 2.001 27 |
表1 单水平算法、标准算法和算法1~3所得近似解的误差
Table 1 Errors of approximate solutions by one-level algorithm, standard algorithm and algorithm 1 to algorithm 3
| 算法 | 1/h | 1/H | CPU/s | ‖▽(u-uh)‖0 | ‖p-ph‖0 | 速度收敛阶 | 压力收敛阶 |
| 单水平算法 | 8 | 0.077 | 1.364 7×10-1 | 2.468 2×10-2 | |||
| 27 | 0.715 | 3.977 0×10-3 | 2.031 3×10-3 | 2.906 64 | 2.053 12 | ||
| 64 | 3.071 | 3.025 5×10-4 | 3.596 1×10-4 | 2.984 79 | 2.006 16 | ||
| 125 | 14.536 | 4.071 3×10-5 | 9.419 0×10-5 | 2.996 16 | 2.001 27 | ||
| 标准算法 | 8 | 4 | 0.181 | 9.069 4×10-1 | 2.497 8×10-2 | ||
| 27 | 9 | 0.305 | 2.424 1×10-2 | 2.031 3×10-3 | 2.977 67 | 2.062 92 | |
| 64 | 16 | 1.65 | 1.832 2×10-3 | 3.596 1×10-4 | 2.992 35 | 2.006 15 | |
| 125 | 25 | 7.258 | 2.465 5×10-4 | 9.419 0×10-5 | 2.996 12 | 2.001 27 | |
| 算法1 | 8 | 4 | 0.063 | 1.521 3×10-1 | 2.471 8×10-2 | ||
| 27 | 9 | 0.296 | 3.978 5×10-3 | 2.031 3×10-3 | 2.995 61 | 2.054 31 | |
| 64 | 16 | 1.664 | 3.025 6×10-4 | 3.596 1×10-4 | 2.985 23 | 2.006 16 | |
| 125 | 25 | 7.494 | 4.071 3×10-5 | 9.419 0×10-5 | 2.996 17 | 2.001 27 | |
| 算法2 | 8 | 4 | 0.065 | 1.510 8×10-1 | 2.471 4×10-2 | ||
| 27 | 9 | 0.319 | 3.978 1×10-3 | 2.031 3×10-3 | 2.989 99 | 2.05417 | |
| 64 | 16 | 1.811 | 3.025 6×10-4 | 3.596 1×10-4 | 2.985 13 | 2.00616 | |
| 125 | 25 | 8.058 | 4.071 3×10-5 | 9.419 0×10-5 | 2.996 17 | 2.00127 | |
| 算法3 | 8 | 4 | 0.062 | 1.364 4×10-1 | 2.468 3×10-2 | ||
| 27 | 9 | 0.29 | 3.977 0×10-3 | 2.031 3×10-3 | 2.906 42 | 2.053 15 | |
| 64 | 16 | 1.62 | 3.025 5×10-4 | 3.596 1×10-4 | 2.984 79 | 2.006 16 | |
| 125 | 25 | 7.275 | 4.071 3×10-5 | 9.419 0×10-5 | 2.996 16 | 2.001 27 |
| 算法 | ν | CPU/s | ‖▽(u-uh)‖0 | ‖p-ph‖0 |
| 算法1 | 1 | 7.276 | 2.246 1×10-6 | 9.419 0×10-5 |
| 10-1 | 7.319 | 1.268 4×10-5 | 9.419 0×10-5 | |
| 10-2 | 7.494 | 4.071 3×10-5 | 9.419 0×10-5 | |
| 10-3 | 7.466 | 3.394 0×10-4 | 9.419 0×10-5 | |
| 10-4 | 8.023 | 5.379 9×10-3 | 9.419 4×10-5 | |
| 算法2 | 1 | 7.846 | 2.246 1×10-6 | 9.419 0×10-5 |
| 10-1 | 7.855 | 1.268 4×10-5 | 9.419 0×10-5 | |
| 10-2 | 8.058 | 4.071 3×10-5 | 9.419 0×10-5 | |
| 10-3 | 8.043 | 3.394 0×10-4 | 9.419 0×10-5 | |
| 10-4 | 8.599 | 5.260 0×10-3 | 9.419 4×10-5 | |
| 算法3 | 1 | 7.247 | 2.246 1×10-6 | 9.419 0×10-5 |
| 10-1 | 7.085 | 1.268 4×10-5 | 9.419 0×10-5 | |
| 10-2 | 7.275 | 4.071 3×10-5 | 9.419 0×10-5 | |
| 10-3 | 7.22 | 3.390 9×10-4 | 9.419 0×10-5 | |
| 10-4 | 7.778 | 3.177 4×10-3 | 9.419 0×10-5 |
表2 不同黏性系数下算法1~3的数值结果
Table 2 Numerical results of algorithm 1 to algorithm 3 with different viscosity
| 算法 | ν | CPU/s | ‖▽(u-uh)‖0 | ‖p-ph‖0 |
| 算法1 | 1 | 7.276 | 2.246 1×10-6 | 9.419 0×10-5 |
| 10-1 | 7.319 | 1.268 4×10-5 | 9.419 0×10-5 | |
| 10-2 | 7.494 | 4.071 3×10-5 | 9.419 0×10-5 | |
| 10-3 | 7.466 | 3.394 0×10-4 | 9.419 0×10-5 | |
| 10-4 | 8.023 | 5.379 9×10-3 | 9.419 4×10-5 | |
| 算法2 | 1 | 7.846 | 2.246 1×10-6 | 9.419 0×10-5 |
| 10-1 | 7.855 | 1.268 4×10-5 | 9.419 0×10-5 | |
| 10-2 | 8.058 | 4.071 3×10-5 | 9.419 0×10-5 | |
| 10-3 | 8.043 | 3.394 0×10-4 | 9.419 0×10-5 | |
| 10-4 | 8.599 | 5.260 0×10-3 | 9.419 4×10-5 | |
| 算法3 | 1 | 7.247 | 2.246 1×10-6 | 9.419 0×10-5 |
| 10-1 | 7.085 | 1.268 4×10-5 | 9.419 0×10-5 | |
| 10-2 | 7.275 | 4.071 3×10-5 | 9.419 0×10-5 | |
| 10-3 | 7.22 | 3.390 9×10-4 | 9.419 0×10-5 | |
| 10-4 | 7.778 | 3.177 4×10-3 | 9.419 0×10-5 |
| 算法 | α | CPU/s | ‖▽(u-uh)‖0 | ‖p-ph‖0 |
| 算法2 | 0 | 7.258 | 2.465 5×10-4 | 9.419 0×10-5 |
| 10-2 | 7.296 | 1.268 4×10-4 | 9.419 0×10-5 | |
| 10-1 | 7.275 | 4.071 3×10-5 | 9.419 0×10-5 | |
| 1 | 7.186 | 3.390 9×10-5 | 9.419 0×10-5 | |
| 10 | 7.247 | 3.177 4×10-5 | 9.419 0×10-5 |
表3 不同稳定化参数下算法2的数值结果
Table 3 Numerical results of algorithm 2 with different stabilization parameters
| 算法 | α | CPU/s | ‖▽(u-uh)‖0 | ‖p-ph‖0 |
| 算法2 | 0 | 7.258 | 2.465 5×10-4 | 9.419 0×10-5 |
| 10-2 | 7.296 | 1.268 4×10-4 | 9.419 0×10-5 | |
| 10-1 | 7.275 | 4.071 3×10-5 | 9.419 0×10-5 | |
| 1 | 7.186 | 3.390 9×10-5 | 9.419 0×10-5 | |
| 10 | 7.247 | 3.177 4×10-5 | 9.419 0×10-5 |
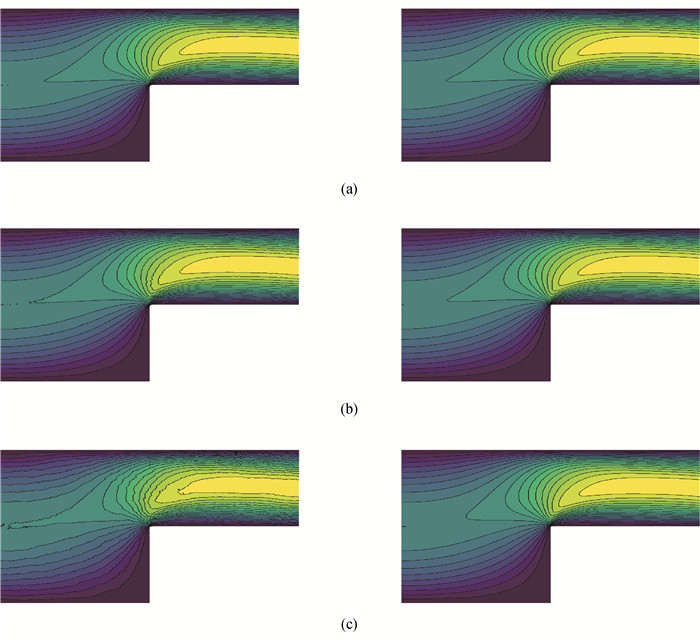
图1 不同ω下标准两水平有限元方法(左)与算法2(右)的速度分量u1 (a)ω=10;(b)ω=102;(c)ω=103
Fig.1 Computed u1 by the standard two-level finite element algorithm (left) and algorithm 2 (right) with different values of ω (a) ω=10; (b) ω=102; (c) ω=103
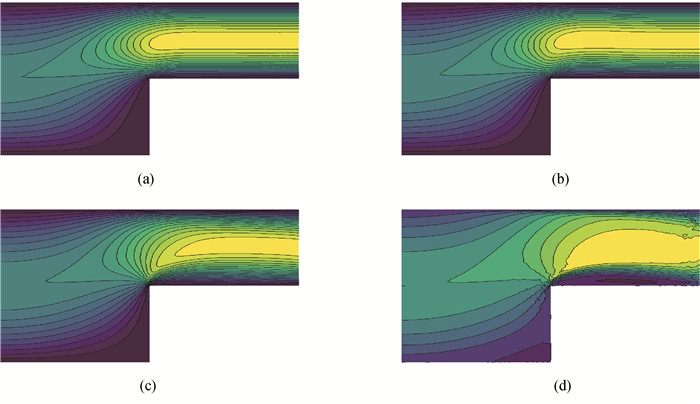
图2 不同ν下算法2计算所得的速度分量u1 (a)ν=1;(b)ν=10-1; (c)ν=10-2; (d)ν=10-3
Fig.2 Computed u1 by algorithm 2 with different values of ν (a)ν=1; (b)ν=10-1; (c)ν=10-2; (d)ν=10-3
| 1 |
XU Jinchao . A novel two-grid method for semilinear elliptic equations[J]. SIAM Journal on Scientific Computing, 1994, 15 (1): 231- 237.
DOI |
| 2 |
XU Jinchao . Two-grid discretization techniques for linear and nonlinear PDEs[J]. SIAM Journal on Numerical Analysis, 1996, 33 (5): 1759- 1777.
DOI |
| 3 | LAYTON W . A two-level discretization method for the Navier-Stokes equations[J]. Computers & Mathematics With Applications, 1993, 26 (2): 33- 38. |
| 4 |
HE Yinnian , LI Kaitai . Two-level stabilized finite element methods for the steady Navier-Stokes problem[J]. Computing, 2005, 74 (4): 337- 351.
DOI |
| 5 | LI Jian , HE Yinnian , XU Hui . A multi-level stabilized finite element method for the stationary Navier-Stokes equations[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196 (29/30): 2852- 2862. |
| 6 |
WEN Juan , HUANG Pengzhan , HE Yaling . The two-level stabilized finite element method based on multiscale enrichment for the stokes eigenvalue problem[J]. Acta Mathematica Scientia, 2021, 41 (2): 381- 396.
DOI |
| 7 | HE Yinnian , WANG Aiwen . A simplified two-level method for the steady Navier-Stokes equations[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197 (17/18): 1568- 1576. |
| 8 | OLSHANSKII M A , REUSKEN A . Grad-div stablilization for stokes equations[J]. Mathematics of Computation, 2004, 73 (248): 1699- 1718. |
| 9 |
DE FRUTOS J , GARCÍA-ARCHILLA B , JOHN V , et al. Analysis of the grad-div stabilization for the time-dependent Navier-Stokes equations with inf-sup stable finite elements[J]. Advances in Computational Mathematics, 2018, 44 (1): 195- 225.
DOI |
| 10 |
AHMED N . On the grad-div stabilization for the steady Oseen and Navier-Stokes equations[J]. Calcolo, 2017, 54 (1): 471- 501.
DOI |
| 11 | 王湛煌, 郑波, 尚月强. 非定常Navier-Stokes方程的并行两水平稳定有限元算法[J]. 计算物理, 2023, 40 (1): 14- 28. |
| 12 | 朱家莉, 尚月强. 不可压缩流的并行两水平稳定有限元算法[J]. 计算物理, 2022, 39 (3): 309- 317. |
| 13 | 丁琪, 尚月强. 非定常Navier-Stokes方程基于两重网格离散的有限元并行算法[J]. 计算物理, 2020, 37 (1): 10- 18. |
| 14 |
LI Wei , HUANG Pengzhan , HE Yinnian . Grad-div stabilized finite element schemes for the fluid-fluid interaction model[J]. Communications in Computational Physics, 2021, 30 (2): 536- 566.
DOI |
| 15 | LAYTON W , XU Shuxian . Stability in 3d of a sparse grad-div approximation of the Navier-Stokes equations[J]. Journal of Mathematical Analysis and Applications, 2022, 516 (1): 126484. |
| 16 | ADAMS R A . Sobolev spaces[M]. New York: Academaic Press, 1975. |
| 17 | SHANG Yueqiang . A two-level subgrid stabilized Oseen iterative method for the steady Navier-Stokes equations[J]. Journal of Computational Physics, 2013, 233, 210- 226. |
| 18 | JOHN V . Finite element methods for incompressible flow problems[M]. Cham: Springer Cham, 2016. |
| 19 | HECHT F . New development in freefem++[J]. Journal of Numerical Mathematics, 2012, 20 (3/4): 251- 265. |
| 20 | HE Yinnian , LI Jian . Convergence of three iterative methods based on the finite element discretization for the stationary Navier-Stokes equations[J]. Computer Methods in Applied Mechanics and Engineering, 2009, 198 (15/16): 1351- 1359. |
| [1] | 王国梁, 郑波, 尚月强. 带阻尼项定常Navier-Stokes方程的并行两水平有限元算法[J]. 计算物理, 2023, 40(5): 535-547. |
| [2] | 王湛煌, 郑波, 尚月强. 非定常Navier-Stokes方程的并行两水平稳定有限元算法[J]. 计算物理, 2023, 40(1): 14-28. |
| [3] | 朱家莉, 尚月强. 不可压缩流的并行两水平稳定有限元算法[J]. 计算物理, 2022, 39(3): 309-317. |
| [4] | 李馨东, 赵英奎, 胡宗民, 姜宗林. 基于第二粘性的Navier-Stokes方程组求解正激波结构[J]. 计算物理, 2020, 37(5): 505-513. |
| [5] | 丁琪, 尚月强. 非定常Navier-Stokes方程基于两重网格离散的有限元并行算法[J]. 计算物理, 2020, 37(1): 10-18. |
| [6] | 张庆福, 姚军, 黄朝琴, 李阳, 王月英. 裂缝性介质多尺度深度学习模型[J]. 计算物理, 2019, 36(6): 665-672. |
| [7] | 温小静, 屈瑜, 陈城钊. 双层开口环的圆二色性数值研究[J]. 计算物理, 2019, 36(3): 357-362. |
| [8] | 葛志昊, 吴慧丽. 体积约束的非局部扩散问题的加罚有限元方法[J]. 计算物理, 2018, 35(2): 161-168. |
| [9] | 杨晓成, 尚月强. 大雷诺数Navier-Stokes方程的两水平亚格子模型稳定化方法[J]. 计算物理, 2017, 34(6): 657-665. |
| [10] | 朱晓钢, 聂玉峰, 王俊刚, 袁占斌. 分数阶对流扩散方程的特征有限元方法[J]. 计算物理, 2017, 34(4): 417-424. |
| [11] | 赵国忠, 蔚喜军, 郭怀民. 二维Lagrangian坐标系下可压气动方程组的间断Petrov-Galerkin方法[J]. 计算物理, 2017, 34(3): 294-308. |
| [12] | 叶珍宝, 朱剑, 周海京. 基于曲四面体单元剖分的CN E-H TDFEM方法[J]. 计算物理, 2016, 33(6): 652-660. |
| [13] | 叶珍宝, 周海京. 基于高阶叠层矢量基函数的E-H时域有限元方法分析谐振腔和波导结构[J]. 计算物理, 2016, 33(3): 333-340. |
| [14] | 叶珍宝, 周海京. 高阶间断伽辽金时域有限元方法分析三维谐振腔[J]. 计算物理, 2015, 32(4): 449-454. |
| [15] | 赵国忠, 蔚喜军, 李珍珍. 多介质流模拟的Runge-Kutta控制体积间断有限元方法[J]. 计算物理, 2014, 31(3): 271-284. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||
版权所有 © 《计算物理》编辑部
地址:北京市海淀区丰豪东路2号 邮编:100094 E-mail:jswl@iapcm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发
