非定常Navier-Stokes方程的并行两水平稳定有限元算法

doi:10.19596/j.cnki.1001-246x.8546

摘要/Abstract

摘要：

使用标准的有限元方法求解非定常Navier-Stokes方程所得速度误差常受压力误差影响，且误差随粘性系数的减少而增大。为了增强压力的鲁棒性，本文引入grad-div稳定项，以提高近似解的精度，提出数值求解非定常Navier-Stokes方程的并行两水平grad-div稳定有限元算法，其时间和空间离散分别采用隐式Euler格式和Galerkin有限元方法。首先在全局粗网格上求解非线性grad-div稳定问题，然后在相互重叠的细网格子区域上并行求解grad-div稳定问题，以校正粗网格解。最后给出数值实验验证理论分析的正确性和算法的有效性。

关键词: 非定常Navier-Stokes方程, grad-div稳定项, 两水平方法, 并行算法, 有限元方法

Abstract:

In numerical solution of unsteady Navier-Stokes equations with standard finite element method, errors of computed velocity are usually affected by pressure errors, where smaller viscosity coefficients lead to greater velocity errors. To improve pressurerobustness, in this paper, we introduce a grad-div stabilization term to improve accuracy of approximate solutions. We present parallel two-level grad-div stabilized finite element algorithms for unsteady Navier-Stokes equations, where implicit Euler scheme and Galerkin finite element methods are used for temporal and spatial discretizations, respectively. At each time step, firstly we solve a nonlinear Navier-Stokes problem with grad-div stabilization on a coarse grid, and then linearized and grad-div stabilized problems are solved with Stokes, Oseen and Newton iterations on overlapping fine grid subdomains in a parallel manner to correct the coarse grid solution. Finally, numerical experiments are given to verify correctness of theoretical predictions and demonstrate effectiveness of the algorithms.

Key words: unsteady Navier-Stokes equations, grad-div stabilization, two-level method, parallel algorithm, finite element method

王湛煌, 郑波, 尚月强. 非定常Navier-Stokes方程的并行两水平稳定有限元算法[J]. 计算物理, 2023, 40(1): 14-28.

Zhanhuang WANG, Bo ZHENG, Yueqiang SHANG. Parallel Two-level Stabilized Finite Element Algorithms for Unsteady Navier-Stokes Equations[J]. Chinese Journal of Computational Physics, 2023, 40(1): 14-28.

图/表 11

表1 算法3.1~3.3的近似解误差

Table 1 Errors of approximate solutions by Algorithms 3.1-3.3

算法	h	H	CPU/s	E_u	E_p	收敛阶
算法3.1	1/27	1/18	7.782	2.283 × 10^-3	2.947 × 10^-3
	1/64	1/32	23.472	4.923 × 10^-4	4.444 × 10^-4	2.044
	1/125	1/50	62.289	1.186 × 10^-4	1.595 × 10^-4	2.060
算法3.2	1/27	1/18	7.553	2.832 × 10^-3	2.943 × 10^-3
	1/64	1/32	23.519	4.923 × 10^-4	4.444 × 10^-4	2.043
	1/125	1/50	63.909	1.186 × 10^-4	1.595 × 10^-4	2.060
算法3.3	1/27	1/18	6.86	2.833 × 10^-3	2.931 × 10^-3
	1/64	1/32	23.222	4.934 × 10^-4	4.456 × 10^-4	2.041
	1/125	1/50	63.645	1.191 × 10^-4	1.586 × 10^-4	2.059

表2 不同ν值下两种算法的误差

Table 2 Errors of two algorithms with different ν

ν	算法3.1		无稳定项的并行算法
ν	E_u	E_p	E_u	E_p
1	1.126 3 × 10^-4	6.216 51 × 10^-4	1.119 99 × 10^-4	5.582 96 × 10^-4
10^-1	1.175 85 × 10^-4	2.083 03 × 10^-4	1.126 32 × 10^-4	2.036 05 × 10^-4
10^-2	1.311 98 × 10^-4	1.933 03 × 10^-4	1.420 51 × 10^-4	2.002 67 × 10^-4
10^-3	3.479 11 × 10^-4	1.946 46 × 10^-4	6.041 92 × 10^-4	1.984 52 × 10^-4
10^-4	5.473 91 × 10^-4	1.966 75 × 10^-4	1.536 08 × 10^-3	1.994 52 × 10^-4
10^-5	5.915 42 × 10^-4	1.970 91 × 10^-4	1.937 1 × 10^-3	1.999 92 × 10^-4
10^-6	5.968 42 × 10^-4	1.971 32 × 10^-4	1.989 61 × 10^-3	2.000 63 × 10^-4

表3 不同子区域下算法3.1的误差

Table 3 Errors of Algorithm 3.1 with different subdomains

子区域数	E_u	E_p
2 × 2	2.283 21 × 10^-3	2.947 28 × 10^-3
2 × 4	2.554 87 × 10^-3	2.092 27 × 10^-3
4 × 4	2.566 64 × 10^-3	2.133 74 × 10^-3

图1 圆柱周围的三角形网格(a) 粗网格; (b)细网格

Fig.1 Triangle partition around a cylinder (a) coarse grid; (b) fine grid

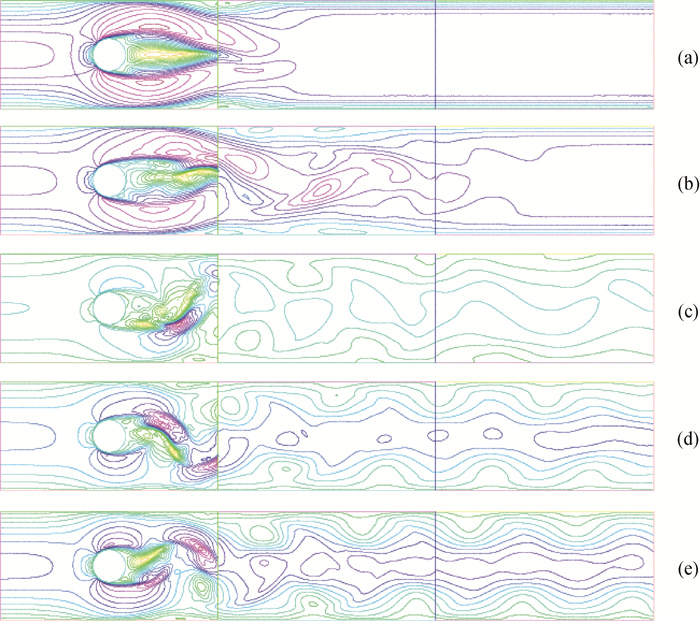
图2 圆柱绕流的速度流线u1 (a) T = 2; (b) T = 4; (c) T = 6; (d) T = 8; (e) T = 10

Fig.2 u1－ velocity of a flow around a circular cylinder (a) T = 2; (b) T = 4; (c) T = 6; (d) T = 8; (e) T = 10

图3 圆柱绕流的速度流线u2 (a) T = 2; (b) T = 4; (c) T = 6; (d) T = 8; (e) T = 10

Fig.3 u2－ velocity of a flow around a circular cylinder (a) T = 2; (b) T = 4; (c) T = 6; (d) T = 8; (e) T = 10

图4 圆柱绕流的等压线(a) T = 2; (b) T = 4; (c) T = 6; (d) T = 8; (e) T = 10

Fig.4 Isobars of a flow around a circular cylinder (a) T = 2; (b) T = 4; (c) T = 6; (d) T = 8; (e) T = 10

图5 方腔驱动流

Fig.5 The lid-driven cavity flow

图6 算法3.1计算Re=100时沿垂直中心线的u1速度分布

Fig.6 u1-velocity profile along the vertical centerline at Re = 100 with Algorithm 3.1

图7 算法3.1计算Re=100时沿水平中心线的u2速度分布

Fig.7 u2-velocity profiles along the horizontal centerline at Re = 100 with Algorithm 3.1

图8 算法3.1计算Re=100时方腔驱动流的流线

Fig.8 Streamlines for the lid-driven cavity flow at Re=100 with Algorithm 3.1

参考文献 32

1	XU J C , ZHOU A H . Local and parallel finite element algorithms based on two-grid discretizations[J]. Mathematics of Computation, 2000, 69, 881- 909.
2	LI Q T , DU G Z . Local and parallel finite element methods based on two-grid discretizations for the nonstationary Navier-Stokes equations[J]. Numerical Algorithms, 2021, 88 (4): 1915- 1936. DOI
3	ZHENG B , SHANG Y Q . Local and parallel stabilized finite element algorithms based on the lowest equal-order elements for the steady Naiver-Stokes equations[J]. Mathematics and Computers in Simulation, 2020, 178, 464- 484. DOI
4	LI L X , ZHAI C L , XIE H , et al. A monolithic preconditioned iterative solver and parallel computing for three-dimensional thermal radiation transport equation[J]. Chinese Journal of Computational Physics, 2021, 38 (3): 269- 279.
5	DING Q , SHANG Y Q . Parallel finite element algorithms based on two-grid discretization for time-dependent Navier-Stokes equations[J]. Chinese Journal of Computational Physics, 2020, 37 (1): 10- 18.
6	LIN M . Pressure robust weak Galerkin finite element methods for Stokes problems[J]. SIAM Journal on Scientific Computing, 2020, 42 (3): 608- 629. DOI
7	JOHN V . Finite element methods for incompressible flow problems[M]. Berlin: Springer Series in Computational Mathematics, Springer-Verlag, 2016.
8	BARRENECHEA G R , VALENTIN F . Consistent local projection stabilized finite element methods[J]. SIAM Journal on Numerical Analysis, 2010, 48 (5): 1801- 1825. DOI
9	BARRENECHEA G R , VALENTIN F . A residual local projection method for the Oseen equation[J]. Computer Methods in Applied Mechanics and Engineering, 2010, 199 (29-32): 1906- 1921. DOI
10	JENKINS E W , JOHN V , LINKE A , et al. On the parameter choice in Grad-div stabilization for Stokes equations[J]. Advances in Computational Mathematics, 2014, 40, 491- 516. DOI
11	OLSHANSKII M A . A low order Galerkin finite element method for the Navier-Stokes equations of steady incompressible flow: A stabilization issue and iterative methods[J]. Computer Methods in Applied Mechanics and Engineering, 2002, 191, 5515- 5536. DOI
12	OLSHANSKII M A , REUSKEN A . Grad-div stabilization for Stokes equations[J]. Mathematics of Computation, 2004, 73, 1699- 1718.
13	FRUTOS J D , ARCHILLA B G , JOHN V , et al. Grad-div stabilization for the evolutionary Oseen problem with inf-sup stable finite elements[J]. Journal of Scientific Computing, 2016, 66, 991- 1024. DOI
14	ZHU J L , SHANG Y Q . A parallel two-level stabilized finite element algorithm for incompressible flows[J]. Chinese Journal of Computational Physics, 2022, 39 (3): 309- 317.
15	LINKE A . A divergence-free velocity reconstruction for incompressible flows[J]. Comptes Rendus Mathematique, 2012, 350 (17-18): 837- 840. DOI
16	LINKE A . On the role of Helmholtz decomposition in mixed methods for incompressible flows and a new variational crime[J]. Computer Methods in Applied Mechanics and Engineering, 2014, 268 (1): 782- 800.
17	LINKE A , MATTHIES G , TOBISKA L . Robust arbitrary order mixed finite element methods for the incompressible Stokes equations with pressure independent velocity errors[J]. Mathematical Modelling and Numerical Analysis, 2016, 50, 289- 309. DOI
18	FRANCA L P , HUGHES T J R . Two classes of mixed finite element methods[J]. Computer Methods in Applied Mechanics and Engineering, 1988, 69 (1): 89- 129. DOI
19	AMHED N . On the Grad-div stabilization for the steady Oseen and Navier-Stokes equations[J]. Calcolo, 2016, 54 (1): 1- 31.
20	LINKE A , REBHOLZ L . On a reduced sparsity stabilization of Grad-div type for incompressible flow problems[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 261 (15): 142- 153.
21	FRUTOS J D , ARCHILLA B G , JOHN V , et al. Analysis of the Grad-div stabilization for the time-dependent Navier-Stokes equations with inf-sup stable finite elements[J]. Advances in Computational Mathematics, 2018, 44 (1): 195- 225. DOI
22	HEYWOOD J G , RANNACHER R . Finite element approximation of the nonstationary Navier Stokes problem Ⅰ: Regularity of solutions and second-order error estimates for spatial discretization[J]. SIAM Journal on Numerical Analysis, 1982, 19 (2): 275- 311. DOI
23	HEYWOOD J G , RANNACHER R . Finite element approximation of the nonstationary Navier Stokes problem Ⅲ: Smoothing property and higher order error estimates for spatial discretization[J]. SIAM Journal on Numerical Analysis, 1988, 25 (3): 489- 512. DOI
24	GIRAULT V , RAVIART P A . Finite element methods for Navier-Stokes equations: Theory and algorithms[M]. Berlin: Springer Verlag, 1986.
25	LI J , HE Y . A new stabilized finite element method for the transient Navier-Stokes equations[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 197 (1): 22- 35.
26	SHANG Y Q , WANG K . Local and parallel finite element algorithms based on two-grid discretizations for the transient Stokes equations[J]. Numerical Algorithms, 2010, 54 (2): 195- 218. DOI
27	HE Y N . A two-level finite element Galerkin method for the nonstationary Navier-Stokes equations Ⅱ[J]. Journal of Computational Mathematics, 2004, 22 (1): 33- 54.
28	HE Y N . The Euler implicit/explicit scheme for the 2D time-dependent Navier-Stokes equations with smooth or non-smooth initial data[J]. Mathematics of Computation, 2006, B 6 (1): 41- 68.
29	HILL A T , SULI E . Approximation of the global attractor for the incompressible Navier-Stokes equations[J]. IMA Journal of Numerical Analysis, 2000, 20 (4): 633- 667. DOI
30	TEMAM R. Navier-Stokes equations [M]. North-Holland, 1984.
31	HECHT F . New development in FreeFem++[J]. Journal of Numerical Mathematics, 2012, 20 (3-4): 251- 265.
32	GHIA U , GHIA K N , SHIN C T . High-re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method[J]. Journal of Computational Physics, 1982, 48 (3): 387- 411. DOI

[1]	王国梁, 郑波, 尚月强. 带阻尼项定常Navier-Stokes方程的并行两水平有限元算法[J]. 计算物理, 2023, 40(5): 535-547.
[2]	胡晓燕, 范征锋. 惯性约束聚变内爆中基于多块结构网格的高效辐射扩散并行算法[J]. 计算物理, 2022, 39(3): 277-285.
[3]	朱家莉, 尚月强. 不可压缩流的并行两水平稳定有限元算法[J]. 计算物理, 2022, 39(3): 309-317.
[4]	蔡颖, 张存波, 刘旭, 范征锋, 刘元元, 徐小文, 张爱清. 二维球坐标系中子输运方程的一种并行SN算法[J]. 计算物理, 2022, 39(2): 143-152.
[5]	丁琪, 尚月强. 非定常Navier-Stokes方程基于两重网格离散的有限元并行算法[J]. 计算物理, 2020, 37(1): 10-18.
[6]	张庆福, 姚军, 黄朝琴, 李阳, 王月英. 裂缝性介质多尺度深度学习模型[J]. 计算物理, 2019, 36(6): 665-672.
[7]	温小静, 屈瑜, 陈城钊. 双层开口环的圆二色性数值研究[J]. 计算物理, 2019, 36(3): 357-362.
[8]	张守慧, 梁栋. 二维抛物型问题的Strang型交替分段区域分裂格式[J]. 计算物理, 2018, 35(4): 413-428.
[9]	葛志昊, 吴慧丽. 体积约束的非局部扩散问题的加罚有限元方法[J]. 计算物理, 2018, 35(2): 161-168.
[10]	杨晓成, 尚月强. 大雷诺数Navier-Stokes方程的两水平亚格子模型稳定化方法[J]. 计算物理, 2017, 34(6): 657-665.
[11]	朱晓钢, 聂玉峰, 王俊刚, 袁占斌. 分数阶对流扩散方程的特征有限元方法[J]. 计算物理, 2017, 34(4): 417-424.
[12]	祁美玲, 杨琼, 王苍龙, 田园, 杨磊. 结构材料辐照损伤的分子动力学程序GPU并行化及优化[J]. 计算物理, 2017, 34(4): 461-467.
[13]	赵国忠, 蔚喜军, 郭怀民. 二维Lagrangian坐标系下可压气动方程组的间断Petrov-Galerkin方法[J]. 计算物理, 2017, 34(3): 294-308.
[14]	叶珍宝, 朱剑, 周海京. 基于曲四面体单元剖分的CN E-H TDFEM方法[J]. 计算物理, 2016, 33(6): 652-660.
[15]	叶珍宝, 周海京. 基于高阶叠层矢量基函数的E-H时域有限元方法分析谐振腔和波导结构[J]. 计算物理, 2016, 33(3): 333-340.