基于深度学习的反演算法: 某些最新进展

doi:10.19596/j.cnki.1001-246x.8992

摘要/Abstract

摘要：

反问题在雷达和声呐探测、医学成像、无损探伤、地球物理勘探等许多领域具有广泛而重要的应用。然而在大多数情况下, 反问题是一个病态的不适定问题, 构造其稳定高效的反演算法极具挑战性。利用未知解的先验信息来构建恰当的正则化策略是应对上述挑战的重要方法之一。传统正则化方法的成功依赖于将未知解准确的先验信息显式地编码到反演算法当中, 但在实际计算中这往往是难以获取和实现的。随着近年来深度学习技术的发展, 直接从数据中学习未知解的先验信息成为了可能, 这将有助于发展高效稳定的反演算法。本文回顾了基于深度学习反演算法的一些最新进展, 重点介绍基于可学习正则化框架的反演算法。此外, 还总结了基于深度学习反演算法的优缺点, 并展望其未来的发展方向。

关键词: 反问题, 反散射问题, 深度学习, 正则化方法, 可学习正则化框架

Abstract:

Inverse problems are of wide and important applications in many areas such as radar and sonar, medical imaging, nondestructive testing and geophysical prospection. Inverse problems are ill-posed problems, so it is challenging to construct stable and highly effective inversion algorithms for them. One of the important methods to tackle this challenging issue is to devise an appropriate regularization strategy based on the a priori information of the unknown solution. The success of traditional regularization methods heavily depends on correctly encoding the a priori information of the unknown solution into the inversion algorithms, but this is in general very difficult in practical computation. With the development of deep learning techniques in recent years, it becomes possible to directly learn the a priori information of the unknown solutions of the inverse problems from data, which is helpful in developing highly effective and stable inversion algorithms. In this paper, we review some recent progres on inversion algorithms based on deep learning, focusing mainly on those based on learnable regularization framework. In addition, we also summarize the advantages and shortcomings of the inversion algorithms based on deep learning, and discuss their future research directions.

Key words: inverse problems, inverse scattering, deep learning, regularization method, learnable regularization framework

李凯, 张波. 基于深度学习的反演算法: 某些最新进展[J]. 计算物理, 2024, 41(6): 717-731.

Kai LI, Bo ZHANG. Inversion Algorithms Based on Deep Learning for Inverse Problems: Some Recent Progresses[J]. Chinese Journal of Computational Physics, 2024, 41(6): 717-731.

图/表 5

图1 NPDHG-CSNet的网络结构

Fig.1 Network architecture of NPDHG-CSNet

图2 NPDHG-CSNet在不同采样率和笛卡尔掩膜下的MRI重构结果

Fig.2 Reconstructed MRI images of NPDHG-CSNet under different sampling rates and the Cartesian sampling mask

图3 投影迭代算法的流程图

Fig.3 Diagram of the projected iterative algorithm

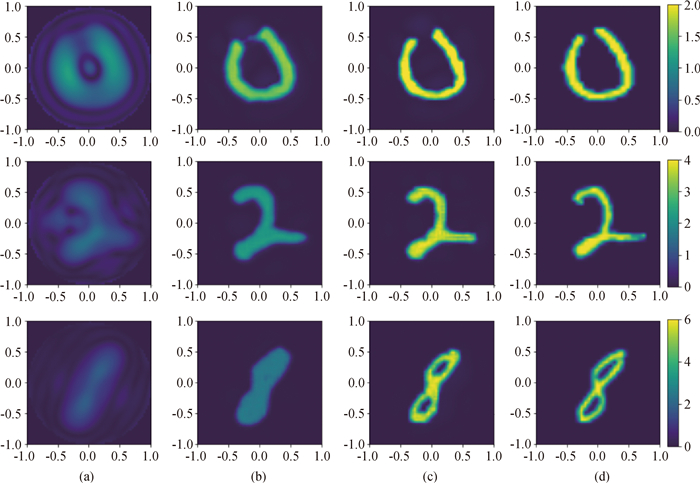
图4 可学习投影迭代算法的重构结果(第3列) (a)Landweber; (b) simplified learned projected scheme; (c) learned projected scheme; (d) ground truth

Fig.4 Reconstructed results by learned projected iterative algorithm (3rd column) (a)Landweber; (b) simplified learned projected scheme; (c) learned projected scheme; (d) ground truth

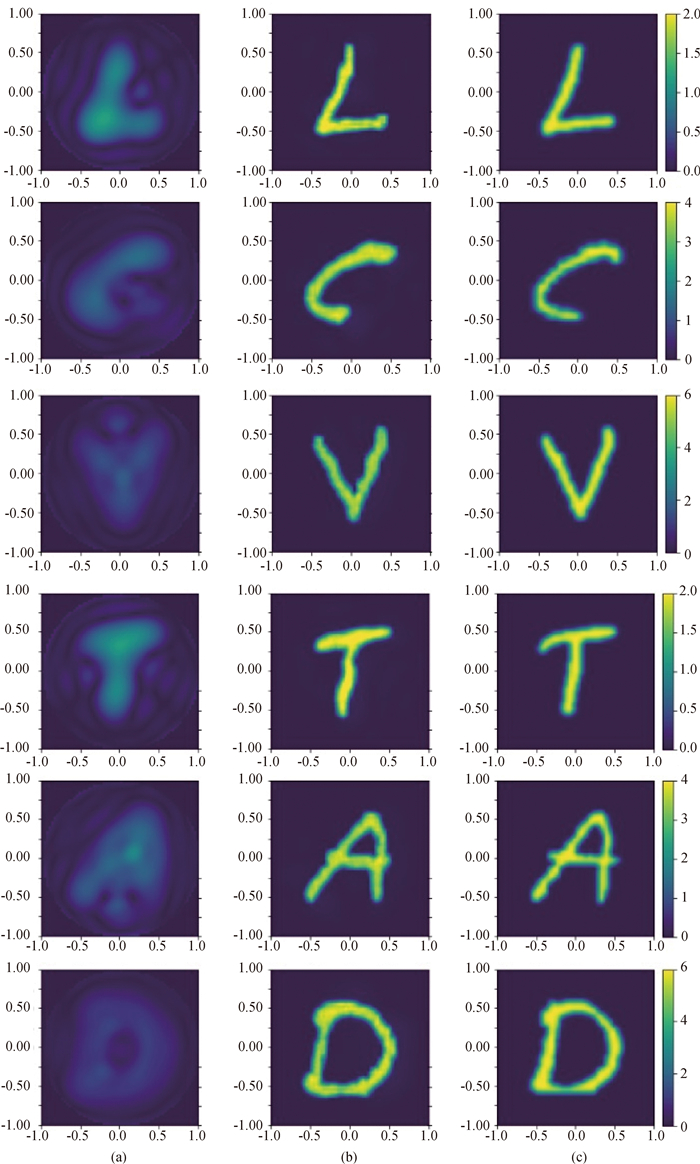
图5 可学习投影迭代算法的泛化性能(a)Landweber; (b)learned projected algorithm; (c) ground truth

Fig.5 Generalization ability of learned projected iterative algorithm (a)Landweber; (b)learned projected algorithm; (c) ground truth

参考文献 86

1	HADAMARD J . Lectures on Cauchy's problems in linear partial differential equations[M]. New Haven: Yale University Press, 1923.
2	TIKHONOV A N . On the stability of inverse problems[J]. Dokl. Akad.Nauk USSR, 1943, 39 (5): 195- 198.
3	TIKHONOV A N . Solution of ill-posed problems and the regularization method[J]. Dokl. Akad. Nauk USSR, 1963, 151 (3): 501- 504.
4	TIKHONOV A N . On the stability of the functional optimization problem[J]. USSR Computational Mathematics and Mathematical Physics, 1966, 6 (4): 28- 33. DOI
5	JOHN F . Numerical solution of the equation of heat conduction for preceding times[J]. Annali di Matematica Pura ed Applicata, 1955, 40 (1): 129- 142. DOI
6	JOHN F . Continuous dependence on data for solutions of partial differential equations with a prescribed bound[J]. Communications on Pure and Applied Mathematics, 1960, 13 (4): 551- 585. DOI
7	NATTERER F . The mathematics of computerized tomography[M]. Philadelphia: SIAM, 2001.
8	NATTERER F , WUBBELING F . Mathematical methods in image reconstruction[M]. Philadelphia: SIAM, 2001.
9	ENGL H W , HANKE M , NEUBAUIER A . Regularization of inverse problems[M]. Dordrecht: Springer, 1996.
10	KIRSCH A . An introduction to the mathematical theory of inverse problems[M]. Cham: Springer, 2011.
11	PLATO R , VAINIKKO G . On the regularization of projection methods for solving Ⅲ-posed problems[J]. Numerische Mathematik, 1990, 57, 63- 79. DOI
12	KALTENBACHER B , NEUBAUER A , SCHERZER O . Iterative regularization methods for nonlinear ill-posed problems[M]. Berlin: Walter De Gruyter, 2008.
13	SCHERZER O , GRASMAIR M , GROSSAUER H , et al. Variational methods in imaging[M]. New York: Springer, 2009.
14	BISSANTZ N , HOHAGE T , MUNK A , et al. Convergence rates of general regularization methods for statistical inverse problems and applications[J]. SIAM Journal on Numerical Analysis, 2007, 45 (6): 2610- 2636. DOI
15	STUART M A . Inverse problems: A Bayesian perspective[J]. Acta Numerica, 2010, 19, 451- 559. DOI
16	TIKHONOV A N , ARSENIN V . Solutions of ill-posed problems[M]. New York: Distributed Solely by Halsted Press, 1977.
17	PHILLIPS D L . A technique for the numerical solution of certain integral equations of the first kind[J]. Journal of the ACM, 1962, 9 (1): 84- 97. DOI
18	RUDIN L I , OSHER S , FATEMI E . Nonlinear total variation based noise removal algorithms[J]. Physica D, 1992, 60 (1/4): 259- 268.
19	BREDIES K , KUNISCH K , VALKONEN T . Properties of L1-TGV2:The one-dimensional case[J]. Journal of Mathematical Analysis and Applications, 2013, 398 (1): 438- 454. DOI
20	CHAMBOLLE A , LIONS P L . Image recovery via total variation minimization and related problems[J]. Numerische Mathematik, 1997, 76 (2): 167- 188. DOI
21	BREDIES K , KUNISCH K , POCK T . Total generalized variation[J]. SIAM Journal on Imaging Sciences, 2010, 3 (3): 492- 526. DOI
22	DAUBECHIES I , DEFRISE M , DE MOL C . An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on Pure and Applied Mathematics, 2004, 57 (11): 1413- 1457. DOI
23	RUBINSTEIN R , BRUCKSTEIN A M , ELAD M . Dictionaries for sparse representation modeling[J]. Proceedings of the IEEE, 2010, 98 (6): 1045- 1057. DOI
24	BRUCKSTEIN A M , DONOHO D L , ELAD M . From sparse solutions of systems of equations to sparse modeling of signals and images[J]. SIAM Review, 2009, 51 (1): 34- 81. DOI
25	ARRIDGE S . Solving inverse problems using data-driven models[J]. Acta Numerica, 2019, 28, 1- 174. DOI
26	BENNING M , BURGER M . Modern regularization methods for inverse problems[J]. Acta Numerica, 2018, 27, 1- 111. DOI
27	LECUN Y , BENGIO Y , HINTON G . Deep learning[J]. Nature, 2015, 521 (7553): 436- 444. DOI
28	RAWAT W , WANG Zenghui . Deep convolutional neural networks for image classification: A comprehensive review[J]. Neural Computation, 2017, 29 (9): 2352- 2449. DOI
29	ZHAO Zhongqiu , ZHENG Peng , XU Shoutao , et al. Object detection with deep learning: A review[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30 (11): 3212- 3232. DOI
30	MINAEE S , BOYKOV Y , PORIKLI F , et al. Image segmentation using deep learning: A survey[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44 (7): 3523- 3542.
31	TIAN Chunwei , FEI Lunke , ZHENG Wenxian , et al. Deep learning on image denoising: An overview[J]. Neural Networks, 2020, 131, 251- 275. DOI
32	ZHANG Kai , ZUO Wangmeng , CHEN Yunjin , et al. Beyond a gaussian denoiser: Residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Processing: A Publication of the IEEE Signal Processing Society, 2017, 26 (7): 3142- 3155. DOI
33	KOETZIER L R , MASTRODICASA D , SZCZYKUTOWICZ T P , et al. Deep learning image reconstruction for CT: Technical principles and clinical prospects[J]. Radiology, 2023, 306 (3): e221257. DOI
34	ADLER J , ÖKTEM O . Solving ill-posed inverse problems using iterative deep neural networks[J]. Inverse Problems, 2017, 33 (12): 124007. DOI
35	GUPTA H , JIN K H , NGUYEN H Q , et al. CNN-Based projected gradient descent for consistent CT image reconstruction[J]. IEEE Transactions on Medical Imaging, 2018, 37 (6): 1440- 1453. DOI
36	LI Housen , SCHWAB J , ANTHOLZER S , et al. NETT: Solving inverse problems with deep neural networks[J]. Inverse Problems, 2020, 36 (6): 065005. DOI
37	ELIASOF M , HABER E , TREISTER E D . Deep regularizers for inverse problems[J]. Inverse Problems, 2024, 40 (1): 015006. DOI
38	LUNZ S, ÖKTEM O, SCHÖNLIEB C B. Adversarial regularizers in inverse problems[C]//Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal, Canada: Curran Associates Inc., 2018: 8516-8525.
39	YANG Yan, SUN Jian, LI Huibin, et al. Deep ADMM-Net for compressive sensing MRI[C]//Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona, Spain: Curran Associates Inc., 2016: 10-18.
40	YANG Yan , SUN Jian , LI Huibin , et al. ADMM-CSNet: A deep learning approach for image compressive sensing[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42 (3): 521- 538. DOI
41	LUNDERVOLD A S , LUNDERVOLD A . An overview of deep learning in medical imaging focusing on MRI[J]. Zeitschrift Fur Medizinische Physik, 2019, 29 (2): 102- 127. DOI
42	CHEN Yutong , SCHÖNLIEB C B , LIÒ P , et al. AI-Based reconstruction for fast MRI—A systematic review and Meta-Analysis[J]. Proceedings of the IEEE, 2022, 110 (2): 224- 245. DOI
43	GVNGÖR A , DAR S U , ÖZTVRK S , et al. Adaptive diffusion priors for accelerated MRI reconstruction[J]. Medical Image Analysis, 2023, 88, 102872. DOI
44	CUI Zhuoxu , ZHU Qingyong , Cheng Jing , et al. Deep unfolding as iterative regularization for imaging inverse problems[J]. Inverse Problems, 2024, 40 (2): 025011. DOI
45	LI K , ZHANG B , ZHANG H . Reconstruction of inhomogeneous media by an iteration algorithm with a learned projector[J]. Inverse Problems, 2024, 40 (7): 075008. DOI
46	CHEN X , WEI Z , LI M , et al. A review of deep learning approaches for inverse scattering problems[J]. Progress in Electromagnetics Research, 2020, 167, 67- 81. DOI
47	ZHOU Yulong , ZHONG Yu , WEI Zhun , et al. An improved deep learning scheme for solving 2-D and 3-D inverse scattering problems[J]. IEEE Transactions on Antennas and Propagation, 2021, 69 (5): 2853- 2863. DOI
48	GUO Rui , LIN Zhichao , SHAN Tao , et al. Physics embedded deep neural network for solving full-wave inverse scattering problems[J]. IEEE Transactions on Antennas and Propagation, 2022, 70 (8): 6148- 6159. DOI
49	LIU Yu , ZHAO Hao , SONG Rencheng , et al. SOM-Net: Unrolling the subspace-based optimization for solving full-wave inverse scattering problems[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60, 1- 15.
50	YANG Fangshu , PHAM T A , GUPTA H , et al. Deep-learning projector for optical diffraction tomography[J]. Optics Express, 2020, 28 (3): 3905- 3921. DOI
51	NING Jianfeng , HAN Fuqun , ZOU Jun . A direct sampling-based deep learning approach for inverse medium scattering problems[J]. Inverse Problems, 2024, 40 (1): 015005. DOI
52	LIN Youzuo , THEILER J , WOHLBERG B . Physics-guided data-driven seismic inversion: Recent progress and future opportunities in full-waveform inversion[J]. IEEE Signal Processing Magazine, 2023, 40 (1): 115- 133. DOI
53	JIN Peng, ZHANG Xitong, CHEN Yinpeng, et al. Unsupervised learning of full-waveform inversion: Connecting CNN and partial differential equation in a loop[DB/OL]. arXiv, 2022: 07584(2022-03-18). https://arxiv.org/abs/2110.07584.
54	LI Shucai , LIU Bin , REN Yuxiao , et al. Deep-learning inversion of seismic data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58 (3): 2135- 2149. DOI
55	WU Yue , LIN Youzuo . InversionNet: An efficient and accurate data-driven full waveform inversion[J]. IEEE Transactions on Computational Imaging, 2020, 6, 419- 433. DOI
56	LUNZ S. Learned regularizers for inverse problems[M]//CHEN Ke, SCHINLIEB C B, TAI Xuecheng, et al. Handbook of Mathematical Models and Algorithms in Computer Vision and Imaging, Cham: Springer, 2022: 1-21.
57	HALTMEIER M, NGUYEN L. Regularization of inverse problems by neural networks[M]. CHEN Ke, SCHINLIEB C B, TAI Xuecheng, et al. Handbook of Mathematical Models and Algorithms in Computer Vision and Imaging, Cham: Springer, 2022: 1-29.
58	MCCANN M T , JIN K H , UNSER M . Convolutional neural networks for inverse problems in imaging: A review[J]. IEEE Signal Processing Magazine, 2017, 34 (6): 85- 95. DOI
59	MONGA V , LI Yuelong , ELDAR Y C . Algorithm unrolling: Interpretable, efficient deep learning for signal and image processing[J]. IEEE Signal Processing Magazine, 2021, 38 (2): 18- 44. DOI
60	WANG Na , SUN Jian . Model meets deep learning in image inverse problems[J]. CSIAM Transactions on Applied Mathematics, 2020, 1 (3): 365- 386. DOI
61	XU R, ZHANG B. NPDHG-CSNets: A deep learning approach for compressive sensing MRI: 报告编号缺失[R]: Preprint, 2024.
62	许锐航. 基于可学习正则化框架的磁共振图像重构算法研究[D]. 北京: 中国科学院大学, 2023.
63	DONOHO D L . Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52 (4): 1289- 1306. DOI
64	VALKONEN T . A primal-dual hybrid gradient method for nonlinear operators with applications to MRI[J]. Inverse Problems, 2014, 30 (5): 055012. DOI
65	SUN Pengpeng , YANG Fangshu , LIANG Hongxian , et al. Full-waveform inversion using a learned regularization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61, 1- 15.
66	COLTON D L , KRESS R . Inverse acoustic and electromagnetic scattering theory[M]. 4rd ed. Cham: Springer, 2019.
67	BAKUSHINSKII A B . The problem of the iterative-regularized Gauss-Newton method[J]. Zhurnal Vychislitel'noi Matematiki Matematicheskoi Fiziki, 1992, 32 (9): 1503- 1509.
68	HYUN C M , KIM H P , LEE S M , et al. Deep learning for undersampled MRI reconstruction[J]. Physics in Medicine and Biology, 2018, 63 (13): 135007. DOI
69	WEI Zhun , LIU Dong , CHEN Xudong . Dominant-current deep learning scheme for electrical impedance tomography[J]. IEEE Transactions on Bio-medical Engineering, 2019, 66 (9): 2546- 2555. DOI
70	LIU Zicheng , ROY M , PRASAD D K , et al. Physics-guided loss functions improve deep learning performance in inverse scattering[J]. IEEE Transactions on Computational Imaging, 2022, 8, 236- 245.
71	ADLER J , ÖKTEM O . Learned primal-dual reconstruction[J]. IEEE Transactions on Medical Imaging, 2018, 37 (6): 1322- 1332.
72	ULYANOV D , VEDALDI A , LEMPITSKY V . Deep image prior[J]. International Journal of Computer Vision, 2020, 128, 1867- 1888.
73	SHU Ziyu , ENTEZARI A . Sparse-view and limited-angle CT reconstruction with untrained networks and deep image prior[J]. Computer Methods and Programs in Biomedicine, 2022, 226, 107167.
74	SUN Yubao , YANG Ying , LIU Qingshan , et al. Learning non-locally regularized compressed sensing network with half-quadratic splitting[J]. IEEE Transactions on Multimedia, 2020, 22 (12): 3236- 3248.
75	JIN Bangti , LI Xiyao , QUAN Qiming , et al. Conductivity imaging from internal measurements with mixed least-squares deep neural networks[J]. SIAM Journal on Imaging Sciences, 2024, 17 (1): 147- 187.
76	HABER E , TENORIO L . Learning regularization functionals-a supervised training approach[J]. Inverse Problems, 2003, 19 (3): 611.
77	AFKHAM B M , CHUNG J , CHUNG M . Learning regularization parameter-maps for variational image reconstruction using deep neural networks and algorithm unrolling[J]. Siam Journal on Imaging Sciences, 2021, 37 (10): 105017.
78	KOFLER A , ALTEKR U GER F , ANTAROU Ba F , et al. Learning regularization parameter-maps for variational image reconstruction using deep neural networks and algorithm unrolling[J]. SIAM Journal on Imaging Sciences, 2023, 16 (4): 2202- 2246.
79	JIA Junxiong , WU Yanni , LI Peijun , et al. Variational inverting network for statistical inverse problems of partial differential equations[J]. Journal of Machine Learning Research, 2023, 24 (1): 9597- 9656.
80	GAO Yu , LIU Hongyu , WANG Xianchao , et al. A bayesian scheme for reconstructing obstacles in acoustic waveguides[J]. Journal of Scientific Computing, 2023, 97 (3): 53.
81	KAWAGUCHI K , BENGIO Y , KAELBLING L . Generalization in deep learning[M]. Cambridge: Cambridge University Press, 2022: 112- 148.
82	NEYSHABUR B, LI Z, BHOJANAPALLI S, et al. Towards understanding the role of over-parametrization in generalization of neural networks[DB/OL]. arXiv, 2018(2018-05-30). https://arxiv.org/pdf/1805.12076.
83	MOHRI M , ROSTAMIZADEH A , TALWALKAR A . Foundations of machine learning[M]. Cambridge: MIT Press, 2018.
84	CHEN D, TACHELLA J, DAVIES M E. Robust equivariant imaging: A fully unsupervised framework for learning to image from noisy and partial measurements[C]//2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). New Orleans, LA, USA: IEEE, 2022: 5637-5646.
85	ZHOU Kaiyang , LIU Ziwei , QIAO Yu , et al. Domain generalization: A survey[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2023, 45 (4): 4396- 4415.
86	FARAHANI A, VOGHOEI S, RASHEED K, et al. A brief review of domain adaptation[C]//Advances in Data Science and Information Engineering: Proceedings From ICDATA 2020 and IKE. Las Vegas, USA: ICDATA, 2021: 877-894.

[1]	刘东, 陈奇隆, 王雪强. 线性积分方程原函数变换深度学习求解方法[J]. 计算物理, 2024, 41(5): 651-662.
[2]	吴国正, 王发杰, 程隋福, 张成鑫. 基于物理信息神经网络的内部声场正反问题数值计算[J]. 计算物理, 2022, 39(6): 687-698.
[3]	卢英东, 韦笃取. 基于遗传注意力机制的DLSTM电力系统混沌预测[J]. 计算物理, 2022, 39(3): 371-378.
[4]	张庆福, 姚军, 黄朝琴, 李阳, 王月英. 裂缝性介质多尺度深度学习模型[J]. 计算物理, 2019, 36(6): 665-672.
[5]	周焕林, 严俊, 余波, 陈豪龙. 基于改进布谷鸟算法识别瞬态热传导问题的导热系数[J]. 计算物理, 2018, 35(2): 212-220.
[6]	何敏, 章礼华, 王其申. 单杠结构差分离散系统的振动反问题[J]. 计算物理, 2016, 33(4): 410-418.
[7]	吴自库, 李福乐, DO Young Kwak. 一维热传导方程热源反问题基于最小二乘法的正则化方法[J]. 计算物理, 2016, 33(1): 49-56.
[8]	王其申, 刘铭徽, 章礼华. 杆的离散系统的某些混合型振动反问题[J]. 计算物理, 2015, 32(3): 321-326.
[9]	王其申, 刘铭徽, 章礼华, 何敏. 由单个模态构造对称简支梁的抗弯刚度[J]. 计算物理, 2014, 31(2): 216-222.
[10]	吕事桂, 杨立, 范春利, 孙丰瑞, 王为清. 缺陷关联参数红外检测Levenberg-Marquardt改进识别算法研究[J]. 计算物理, 2013, 30(2): 214-220.
[11]	江良, 徐承龙. 非高斯单因子短期利率模型正则化参数估计[J]. 计算物理, 2012, 29(6): 837-844.
[12]	杨鑫, 李润东, 刘汉刚, 王冠博, 王侃. 基于概率迭代的NDP反演方法[J]. 计算物理, 2012, 29(6): 891-900.
[13]	吴磊, 刘全金, 章礼华, 王其申. 外伸梁差分离散系统的模态反问题[J]. 计算物理, 2010, 27(3): 407-412.
[14]	潘文峰, 宗志雄, 尤云祥, 缪国平. 三维海洋波导中散射目标快速声学远场成像[J]. 计算物理, 2010, 27(1): 121-130.
[15]	范春利, 孙丰瑞, 杨立. 二维不规则形状发热型缺陷的红外识别算法[J]. 计算物理, 2009, 26(6): 897-902.