电磁场耦合下Hindmarsh-Rose忆阻神经网络相干共振研究

doi:10.19596/j.cnki.1001-246x.8769

摘要/Abstract

摘要：

基于改进的电磁感应神经元模型, 研究忆阻神经Hindmarsh-Rose (HR)网络的相干共振(CR)现象。模型中除了电耦合连接相邻神经元之间的间隙外, 还使用磁耦合来描述神经元之间的场耦合效应。利用分岔图和相图对稳定点进行动力学分析, 解释了CR出现和放电模式变化的潜在动力学机制。研究发现高斯白噪声可以在忆阻神经元亚临界Hopf分岔附近的静息状态诱导CR, 且CR的出现与噪声强度增大引起的放电模式变化有关。

关键词: Hindmarsh-Rose神经元, 忆阻, 高斯白噪声, 相干共振

Abstract:

Based on the improved electromagnetic induction neuron model, the coherent resonance (CR) phenomenon of the Memristor Hindmarsh-Rose (HR) network is studied. In addition to electrical coupling connecting gaps between adjacent neurons, magnetic coupling is used to describe the effect of field coupling between neurons. The dynamic analysis of the stable point is performed using the bifurcation diagram and phase diagram, and the potential dynamic mechanism of the emergence of CR and the change of discharge mode are explained. It is found that white Gaussian noise can induce CR in the resting state near the subcritical Hopf bifurcation of memristor neurons, and the occurrence of CR is related to the change of firing mode caused by the increase of noise amplitude.

Key words: Hindmarsh-Rose neurons, memristor, Gaussian white noise, coherent resonance

黄微, 韦笃取. 电磁场耦合下Hindmarsh-Rose忆阻神经网络相干共振研究[J]. 计算物理, 2025, 42(1): 98-105.

Wei HUANG, Duqu WEI. Coherent Resonance in Hindmarsh-Rose Neural Network under Electromagnetic Field Coupling[J]. Chinese Journal of Computational Physics, 2025, 42(1): 98-105.

图/表 7

图1 忆阻HR神经网络中任意神经元(i = 50)膜电位分岔图

Fig.1 Bifurcation diagram of neuron (i = 50) in memristor HR neural network

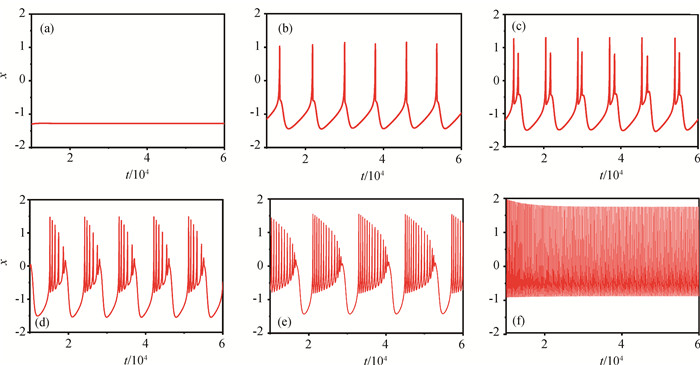
图2 不同I值下，神经元(i = 50)的膜电位时间序列(D = 0、g = 0.002) (a) I = 1.9；(b) I = 2.2；(c) I = 2.7；(d) I = 3.25；(e) I = 3.5；(f) I = 3.8

Fig.2 Time series of membrane potential of neurons (i=50) with different I for D = 0 and g = 0.002 (a) I = 1.9; (b) I = 2.2; (c) I = 2.7; (d) I = 3.25; (e) I = 3.5; (f) I = 3.8

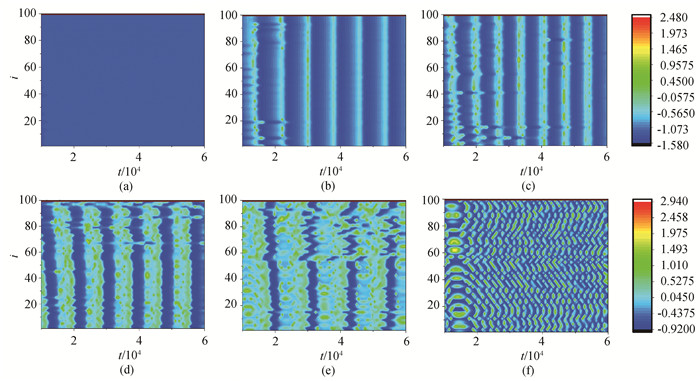
图3 不同I值下，神经网络的空间模式(D = 0、g = 0.002) (a) I = 1.9；(b) I = 2.2；(c) I = 2.7；(d) I = 3.25；(e) I = 3.5；(f) I = 3.8

Fig.3 Spatial mode of neural network with different I for D = 0 and g = 0.002 (a) I = 1.9; (b) I = 2.2; (c) I = 2.7; (d) I = 3.25; (e) I = 3.5; (f) I = 3.8

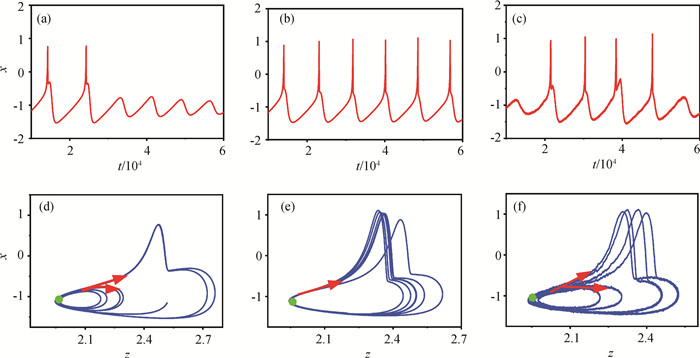
图4 不同D值下，神经元(i = 50)的膜电位放电活动(I = 1.82，g = 0.002) (a) D = 0.0001；(b) D = 0.001；(c) D = 0.01；相平面图：(d) D = 0.0001；(e) D = 0.001；(f) D = 0.01

Fig.4 Membrane potential of neurons (i = 50) with different D for I = 1.82 and g=0.002 (a) D = 0.0001; (b) D = 0.001; (c) D = 0.01; phase plan: (d) D = 0.0001; (e) D = 0.001; (f) D = 0.01

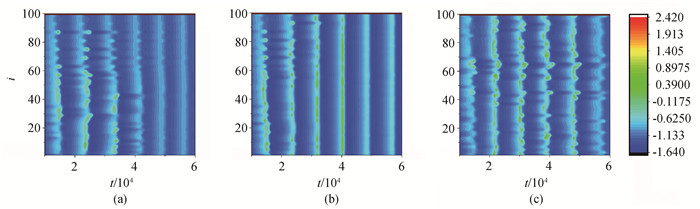
图5 不同D值下，神经网络的空间模式(I = 1.82，g = 0.002) (a) D = 0.0001；(b) D = 0.001；(c) D = 0.01

Fig.5 Spatial patterns of neural networks with different D for I = 1.82 and g = 0.002 (a) D = 0.0001; (b) D = 0.001; (c) D = 0.01

图6 不同I和g对D诱发相干共振系数cv的影响(a)电流I；(b)耦合强度g

Fig.6 Effects of different I and g on cv induced by D (a) I; (b) g

图7 双参数下cv的变化(a)I和D；(b) g和D

Fig.7 Variations of cv with dual parameters (a) I and D); (b) g and D

参考文献 28

1	FAISAL A A , SELEN L P J , WOLPERT D M . Noise in the nervous system[J]. Nature Reviews Neuroscience, 2008, 9, 292- 303. DOI
2	潘剑, 郭照立, 陈松泽. 从噪声数据学习偏微分方程的复合神经网络[J]. 计算物理, 2022, 39 (2): 223- 232.
3	RUNNOVA A E , HRAMOV A E , GRUBOV V V , et al. Theoretical background and experimental measurements of human brain noise intensity in perception of ambiguous images[J]. Chaos Solitons & Fractals, 2016, 93, 201- 206.
4	LI Yuxi , WEI Zhouchao , KAPITANIAK T , et al. Stochastic bifurcation and chaos analysis for a class of ships rolling motion under non-smooth perturbation and random excitation[J]. Ocean Engineering, 2022, 266, 112859. DOI
5	TAN Fei , ZHOU Lili . Analysis of random synchronization under bilayer derivative and nonlinear delay networks of neuron nodes via fixed time policies[J]. ISA Transactions, 2022, 129, 114- 127. DOI
6	GAMMAITONI L , HÄNGGI P , JUNG P , et al. Stochastic resonance[J]. Reviews of Modern Physics, 1998, 70 (1): 223- 287. DOI
7	PIKOVSKY A S , KURTHS J . Coherence resonance in a noise-driven excitable system[J]. Physical Review Letters, 1997, 78 (5): 775- 778. DOI
8	PISARCHIK A N , HRAMOV A E . Coherence resonance in neural networks: Theory and experiments[J]. Physics Reports, 2023, 1000, 1- 57. DOI
9	MA Jinzhong , XU Yong , XU Wei , et al. Slowing down critical transitions via Gaussian white noise and periodic force[J]. Science China Technological Sciences, 2019, 62 (12): 2144- 2152. DOI
10	LI Li , ZHAO Zhiguo . White-noise-induced double coherence resonances in reduced Hodgkin-Huxley neuron model near subcritical Hopf bifurcation[J]. Physical Review E, 2022, 105 (3/1): 034408.
11	MA Xu , LI Chunbiao , WANG Ran , et al. Memristive computation-oriented chaos and dynamics control[J]. Frontiers in Physics, 2021, 9, 759913. DOI
12	GEFFERT P M , ZAKHAROVA A , VÜLLINGS A , et al. Modulating coherence resonance in non-excitable systems by time-delayed feedback[J]. The European Physical Journal B, 2014, 87, 291. DOI
13	ZAKHAROVA A , VADIVASOVA T , ANISHCHENKO V , et al. Stochastic bifurcations and coherencelike resonance in a self-sustained bistable noisy oscillator[J]. Physical Review E, 2010, 81 (1): 011106. DOI
14	KATO Y , NAKAO H . Quantum coherence resonance[J]. New Journal of Physics, 2021, 23, 043018. DOI
15	XU Ying , LIU Minghua , ZHU Zhigang , et al. Dynamics and coherence resonance in a thermosensitive neuron driven by photocurrent[J]. Chinese Physics B, 2020, 29 (9): 098704. DOI
16	EGGERMONT J J . Is there a neural code?[J]. Neuroscience & Biobehavioral Reviews, 1998, 22 (2): 355- 370.
17	HORWITZ B , BRAUN A R . Brain network interactions in auditory, visual and linguistic processing[J]. Brain and Language, 2004, 89 (2): 377- 384. DOI
18	VAN WIJK B C M , BEEK P J , DAFFERTSHOFER A . Neural synchrony within the motor system: What have we learned so far?[J]. Frontiers in Human Neuroscience, 2012, 6, 252.
19	XU Quan , CHEN Xiongjian , CHEN Bei , et al. Dynamical analysis of an improved FitzHugh-Nagumo neuron model with multiplier-free implementation[J]. Nonlinear Dynamics, 2023, 111 (9): 8737- 8749. DOI
20	罗佳, 孙亮, 乔印虎. 忆阻突触耦合环形Hopfield神经网络动力学分析及其电路实现[J]. 计算物理, 2022, 39 (1): 109- 117.
21	CHUA L . Memristor—The missing circuit element[J]. IEEE Transactions on Circuit Theory, 1971, 18 (5): 507- 519. DOI
22	ZHANG Sen , LI Chunbiao , ZHENG Jiahao , et al. Memristive autapse-coupled neuron model with external electromagnetic radiation effects[J]. IEEE Transactions on Industrial Electronics, 2023, 70 (11): 11618- 11627. DOI
23	MA Xu , LI Chunbiao , LI Yaning , et al. Rotation control of an HR neuron with a locally active memristor[J]. The European Physical Journal Plus, 2022, 137, 542. DOI
24	YU Xihong , BAO Han , CHEN Mo , et al. Energy balance via memristor synapse in Morris-Lecar two-neuron network with FPGA implementation[J]. Chaos Solitons & Fractals, 2023, 171, 113442.
25	周倩, 韦笃取. 场耦合忆阻神经网络的电活动[J]. 计算物理, 2020, 37 (6): 750- 756.
26	STORACE M , LINARO D , DE LANGE E . The Hindmarsh-Rose neuron model: Bifurcation analysis and piecewise-linear approximations[J]. Chaos, 2008, 18 (3): 033128. DOI
27	FU F , LIU L H , WANG L . Evolutionary prisoner's dilemma on heterogeneous newman-watts small-world network[J]. The European Physical Journal B, 2007, 56, 367- 372. DOI
28	高正, 邹艳丽, 胡均万, 等. 基于复杂网络理论的电网耦合强度分配策略[J]. 计算物理, 2022, 39 (5): 579- 588.

[1]	陈吉, 徐毅, 刘进福, 刘涛. 呈现超级多稳态忆阻系统的动力学与实现[J]. 计算物理, 2024, 41(4): 523-534.
[2]	赵双, 陈湘军, 张云贞. 忆阻Lorenz混沌系统的动力学分析与电路实现[J]. 计算物理, 2024, 41(2): 268-276.
[3]	刘丽君, 韦笃取. 忆阻Rulkov神经网络同步研究[J]. 计算物理, 2023, 40(3): 389-400.
[4]	孙亮, 罗佳, 乔印虎. 忆阻Hopfield神经网络的初值位移调控动力学及其图像加密应用[J]. 计算物理, 2023, 40(1): 106-116.
[5]	唐利红, 贺宗梅, 姚延立. 具有隐藏超级多稳定性的磁感应HR神经元及其电路实现[J]. 计算物理, 2022, 39(5): 589-597.
[6]	唐利红, 贺宗梅, 姚延立. 忆阻Hopfield神经网络动力学分析及其电路实现[J]. 计算物理, 2022, 39(2): 244-252.
[7]	罗佳, 孙亮, 乔印虎. 忆阻突触耦合环形Hopfield神经网络动力学分析及其电路实现[J]. 计算物理, 2022, 39(1): 109-117.
[8]	周倩, 韦笃取. 场耦合忆阻神经网络的电活动[J]. 计算物理, 2020, 37(6): 750-756.
[9]	黄志精, 白婧, 唐国宁. 单向耦合神经元网络中螺旋波的自发形成机制[J]. 计算物理, 2020, 37(5): 612-622.
[10]	刘娣, 杨芳艳, 周国鹏, 李清都, 廖晓昕. 一类四维忆阻混沌电路的动力学行为分析[J]. 计算物理, 2018, 35(4): 458-468.
[11]	王伟, 曾以成, 陈争, 孙睿婷. 忆阻器混沌电路产生的共存吸引子与Hopf分岔[J]. 计算物理, 2017, 34(6): 747-756.
[12]	余世成, 曾以成, 李志军. 一种二次型忆阻器四阶混沌电路[J]. 计算物理, 2015, 32(6): 735-743.
[13]	谭志平, 杨红姣, 刘奇能, 曾以成. 最简荷控型忆阻器混沌电路的设计及实现[J]. 计算物理, 2015, 32(4): 496-504.