A Compound Neural Network for Learning Partial Differential Equations from Noisy Data

doi:10.19596/j.cnki.1001-246x.8364

Abstract

Abstract:

A compound neural network method, NN-PDE(neural network-partial differential equations), is proposed for data preprocessing and learning partial differential equation. NN-PDE uses one sub network to preprocess noisy data, and another one to couple information of the alternative equations to learn the underlying governing equation. These two sub networks are merged into one compound network so that it can process noisy data more efficiently and effectively to reduce the influence of noise. Noisy data generated from various physical equations (such as Burgers equation, Korteweg-de Vries(KdV) equation, Kuramoto-Sivashinsky(KS) equation and Navier-Stokes(NS) equation) are studied with NN-PDE, and accurate governing equations are obtained.

Key words: noisy data, compound neural network, partial differential equations

Jian PAN, Zhaoli GUO, Songze CHEN. A Compound Neural Network for Learning Partial Differential Equations from Noisy Data[J]. Chinese Journal of Computational Physics, 2022, 39(2): 223-232.

Figures/Tables 10

Fig.1 Structure of a fully connected neural network

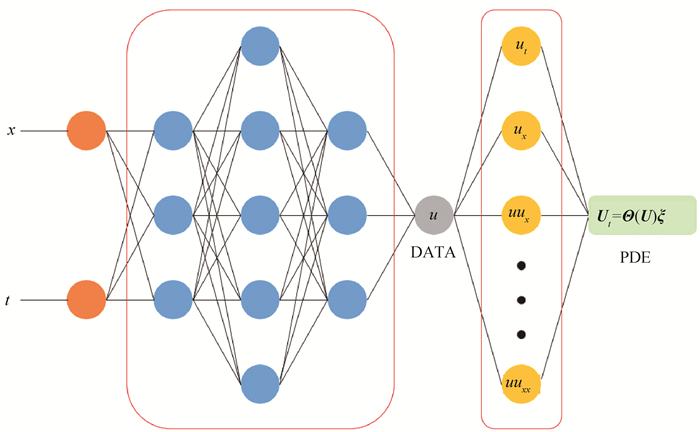
Fig.2 Structure of a compound neural network (The blue part represents the network that approximates solution of the equation. The yellow part represents the constructed candidate library. The DATA part represents residual of the data. The PDE part represents residual of the constructed governing equation.)

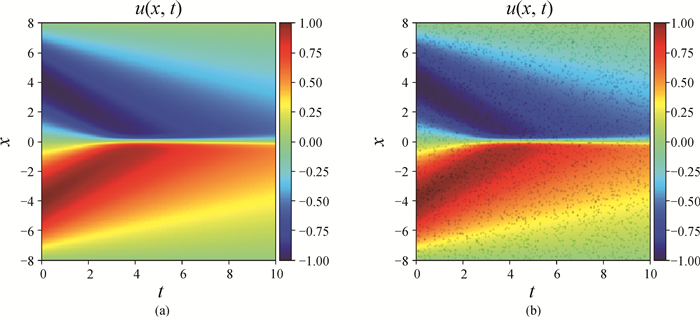
Fig.3 (a) Solution of Burgers equation in the form of heat map and (b) a portion of the map indicating 3000 data selected randomly from the dataset (The background represents the solution u in the dataset by heat map, and the black dots are selected data.)

Table 1 Performance of NN-PDE and STRidge in different noises for Burgers equation ut=- uux+0.1uxx

噪声数据量	NN-PDE	STRidge
无	u_t=- 0.9988 uu_x+0.0999 u_xx	u_t=- 1.001 uu_x+0.102 u_xx
1%	u_t=- 0.9965 uu_x+0.0997 u_xx	u_t=- 0.960 uu_x+0.102 u_xx
5%	u_t=- 0.9992 uu_x+0.1003 u_xx	u_t=- 0.824 uu_x+0.117 u_xx - 0.06 u²u_xx
10%	u_t=- 0.9789 uu_x+0.0998 u_xx	无法得到简约的方程

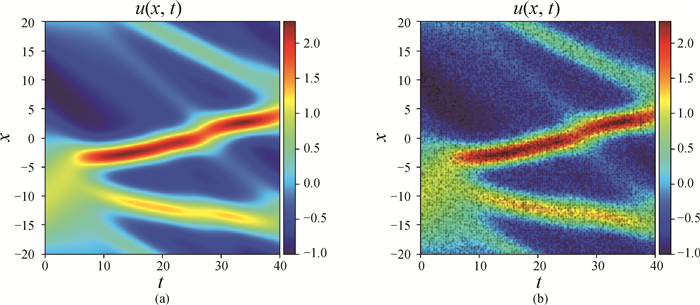
Fig.4 (a) Solution of KdV equation in the form of heat map and (b) a portion of the map indicating 25 000 data selected randomly from the dataset (The background represents solution u in the dataset by heat map, and the black dots are selected data.)

Table 2 Performance of NN-PDE and STRidge in different noises for KdV equation ut=- uux - uxxx

噪声数据量	NN-PDE	DL-PDE
无	u_t=- 0.9995 uu_x - 0.9995 u_xxx	u_t=- 0.993 uu_x - 0.996 u_xxx
1%	u_t=- 0.9986 uu_x - 0.9991 u_xxx	u_t=- 0.986 uu_x - 0.985 u_xxx
5%	u_t=- 0.9995 uu_x - 0.9973 u_xxx	u_t=- 0.968 uu_x - 0.974 u_xxx
10%	u_t=- 1.0018 uu_x - 1.0023 u_xxx	u_t=- 0.940 uu_x - 0.936 u_xxx

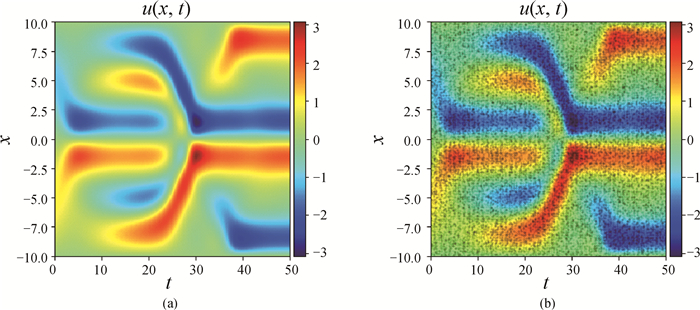
Fig.5 (a) Solution of KS equation in the form of heat map and (b) a portion of the map indicating 25 000 data selected randomly from the dataset (The background represents the solution u in the dataset by heat map, and the black dots are selected data.)

Table 3 Performance of NN-PDE and STRidge in different noises for KS equation ut=- uux - uxx - uxxxx

噪声数据量	控制方程
无	u_t=- 0.9969 uu_x - 0.9966 u_xx - 0.9972 u_xxxx
1%	u_t=- 0.9982 uu_x - 0.9954 u_xx - 0.9964 u_xxxx
5%	u_t=- 0.9962 uu_x - 0.9946 u_xx - 0.9955 u_xxxx
10%	u_t=- 0.9780 uu_x - 1.0020 u_xx - 0.9964 u_xxxx

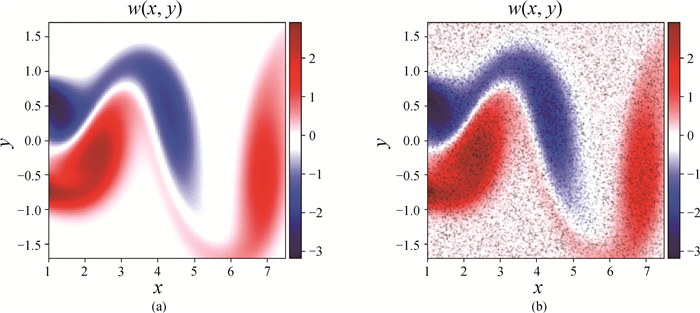
Fig.6 (a) Solution of NS equation in the form of heat map and (b) a portion of the map indicating 50 000 data selected randomly from the dataset (The background represents the solution w in the dataset by heat map, and the black dots are selected data.)

Table 4 Performance of NN-PDE and STRidge in different noises for NS equation wt=- uwx - vwy+0.01(wxx+wyy)

噪声数据量	控制方程
无	w_t=- 0.9995 uw_x- 0.9986 vw_y+0.0100 w_xx+0.0100 w_yy
1%	w_t=- 0.9993 uw_x- 0.9982 vw_y+0.0100 w_xx+0.0100 w_yy
5%	w_t=- 0.9988 uw_x- 0.9919 vw_y+0.0100 w_xx+0.0100 w_yy
10%	w_t=- 0.9936 uw_x- 0.9729 vw_y+0.0095 w_xx+0.0108 w_yy

References 23

1	BRUNTON S L , PROCTOR J L , KUTZ J N . Discovering governing equations from data by sparse identification of nonlinear dynamical systems[J]. Proceedings of the National Academy of Sciences, 2016, 113 (15): 3932- 3937. DOI
2	SCHAEFFER H . Learning partial differential equations via data discovery and sparse optimization[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2017, 473 (2197): 20160446. DOI
3	RUDY S H , BRUNTON S L , PROCTOR J L , et al. Data-driven discovery of partial differential equations[J]. Science Advances, 2017, 3 (4): e1602614. DOI
4	MANGAN N M , KUTZ J N , BRUNTON S L , et al. Model selection for dynamical systems via sparse regression and information criteria[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2017, 473 (2204): 20170009. DOI
5	BONINSEGNA L , NUSKE F , CLEMENTI C . Sparse learning of stochastic dynamic equations[J]. The Journal of Chemical Physics, 2018, 148 (24): 241723. DOI
6	QUADE M , ABEL M , KUTZ J N , et al. Sparse identification of nonlinear dynamics for rapid model recovery[J]. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2018, 28 (6): 063116. DOI
7	RUDY S , ALLA A , BRUNTON S L , et al. Data-driven identification of parametric partial differential equations[J]. SIAM Journal on Applied Dynamical Systems, 2019, 18 (2): 643- 660. DOI
8	CHAMPION K , LUSCH B , KUTZ J N , et al. Data-driven discovery of coordinates and governing equations[J]. Proceedings of the National Academy of Sciences of the United States of America, 2019, 116 (45): 22445- 22451. DOI
9	BERG J , NYSTROM K . Data-driven discovery of PDEs in complex datasets[J]. Journal of Computational Physics, 2019, 384, 239- 252. DOI
10	CHANG H , ZHANG D . Machine learning subsurface flow equations from data[J]. Computational Geosciences, 2019, 23 (5): 895- 910. DOI
11	CHANG H , ZHANG D . Identification of physical processes via combined data-driven and data-assimilation methods[J]. Journal of Computational Physics, 2019, 393, 337- 350. DOI
12	CHARTRAND R . Numerical differentiation of noisy, nonsmooth data[J]. ISRN Applied Mathematics, 2011, 2011, 1023- 1033.
13	BRUNO O , HOCH D . Numerical differentiation of approximated functions with limited order-of-accuracy deterioration[J]. SIAM Journal on Numerical Analysis, 2012, 50 (3): 1581- 1603. DOI
14	KNOWLES I, RENKA R J. Methods for numerical differentiation of noisy data[J]. Electronic Journal of Differential Equations, Conference 21(2014): 235-246.
15	SCHAEFFER H , MCCALLA S G . Sparse model selection via integral terms[J]. Physical Review E, 2017, 96 (2): 023302. DOI
16	RAISSI M . Machine learning of linear differential equations using Gaussian processes[J]. Journal of Computational Physics, 2017, 348, 683- 693. DOI
17	RAISSI M , KARNIADAKIS G E . Hidden physics models: Machine learning of nonlinear partial differential equations[J]. Journal of Computational Physics, 2018, 357, 125- 141. DOI
18	RAISSI M , PERDIKARIS P , KARNIADAKIS G E . Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378, 686- 707. DOI
19	RAISSI M . Deep hidden physics models: Deep learning of nonlinear partial differential equations[J]. Journal of Machine Learning Research, 2018, 19 (25): 1- 24.
20	LONG Z , LU Y , MA X , et al. PDE-NET: Learning PDEs from data[J]. PMLR, 2018, 80, 3208- 3216.
21	XU H . DL-PDE: Deep-learning based data-driven discovery of partial differential equations from discrete and noisy data[J]. Communications in Computational Physics, 2021, 29 (3): 698- 728. DOI
22	CYBENKO G . Approximation by superpositions of a sigmoidal function[J]. Mathematics of Control Signals & Systems, 1989, 2 (4): 303- 314.
23	GLOROT X , BENGIO Y . Understanding the difficulty of training deep feedforward neural networks[J]. Journal of Machine Learning Research, 2010, 9, 249- 256.

[1]	MEI Shu-li, LU Qi-shao, ZHANG Sen-wen. An Adaptive Wavelet Precise Integration Method for Partial Differential Equations [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2004, 21(6): 523-530.
[2]	Zhang Zhengke, Zhuang Fenggan, Zhu Ziqiang, Luo Shijun. RESEARCH OF GRID SPACING AND ORTHOGONALITY CONTROL IN THREE DIMENSIONAL FLOWS AROUND A WING BODY TAIL COMBINATION [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 1997, 14(2): 247-252.