Deep Learning Method for Solving Linear Integral Equations Through Primitive Function Transformation

doi:10.19596/j.cnki.1001-246x.8813

Abstract

Abstract:

Due to factors such as limited integral terms and approximations, solving integral equations using classical numerical methods is often more challenging than solving differential equations. This paper proposes a theory of solving linear integral equations through the transformation of primitive functions using deep learning. By transforming the integrand into a primitive function, the integral equation is converted into a purely differential equation. The paper also provides a method for determining the initial conditions of the primitive function and a technique for generating the neural network loss function. After approximating the primitive function using deep learning with neural networks, the derivative of the primitive function is calculated and transformed according to the form of the integral kernel, ultimately obtaining the numerical solution of the unknown function in the integral equation. Through numerical experiments on various typical examples, the paper demonstrates that the proposed theory and key techniques exhibit good accuracy and applicability, thereby opening up new technical approaches for the numerical solution of linear integral equations.

Key words: deep learning, linear integral equation, degenerate kernel, transformation of primitive functions, loss function, numerical validation

CLC Number:

TL329

Dong LIU, Qilong CHEN, Xueqiang WANG. Deep Learning Method for Solving Linear Integral Equations Through Primitive Function Transformation[J]. Chinese Journal of Computational Physics, 2024, 41(5): 651-662.

Figures/Tables 11

Fig.1 Iterative solution process of multi-integral term original function transformation

Table 1 Loss function, sample generation method and numerical operation results of the first kind of Volterra equation

损失函数类型	约束形式	样本数量	样本生成方式	损失函数权重	σ_MSE/10^-8	σ_{MSE, max}/10^-6	Loss/10^-8
控制方程F_f－loss	方程(16)	5 000	随机分布	P_f= 1	2.169 4	6.105 1	2.239 1
原函数定解约束F_d－loss	t=0, F₀(x, 0) = 0	150	固定	P_d =50

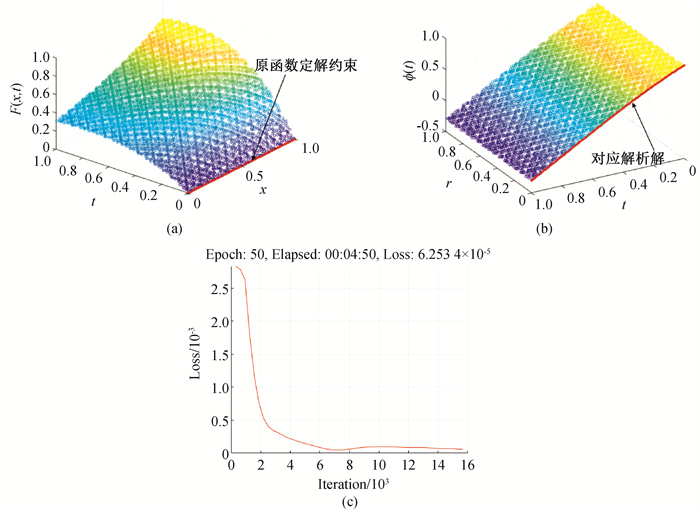
Fig.2 Numerical results of the first kind Volterra equation (a) scatterplot of the original function distribution of ascending order; (b) scatterplot of distribution of numerical solution of equation; (c) Fall-loss trend graph with time (first 50 times)

Table 2 Loss function, sample generation method and numerical operation results of the second type of Fredholm equation

损失函数类型	约束形式	样本数量	样本生成方式	损失函数权重	σ_MSE/10^-8	σ_{MSE, max}/10^-7	Loss/10^-8
控制方程F_f－loss	方程(9)	5 000	随机分布	1	1.251 5	7.841 6	2.683 0
原函数确定解约束F_d－loss	t=0, F₀(x, 0)=0	150	固定	50

Fig.3 Numerical results ot the second kind Fredholm equation (a) scatterplot of the original function distribution of ascending order; (b) scatterplot of distribution of the numerical solution of the equation; (c) Fall-loss trend graph with time (first 50 times)

Table 3 Loss function, sample generation method and numerical operation results of degenerate kernel Fredholm equation

损失函数来源	约束形式	样本数量	样本生成方式	损失函数权重	σ_MSE/10^-8	σ_{MSE, max}/10^-6	Loss/10^-9
控制方程F_f-loss－1; F_f-loss－2	方程(17)、(18)	1 000	随机分布	1	6.006 3(图 4(a))	6.284 1(图 4(a))	28.289(图 4(a))
原函数定解约束F_d－loss－1; F_d－loss－2	t₁=0, F₀₁(0)=0;t₂=0, F₀₂(0)=0	1	固定	30	4.906 7(图 4(b))	9.261 8(图 4(b))	7.335 6(图 4(b))

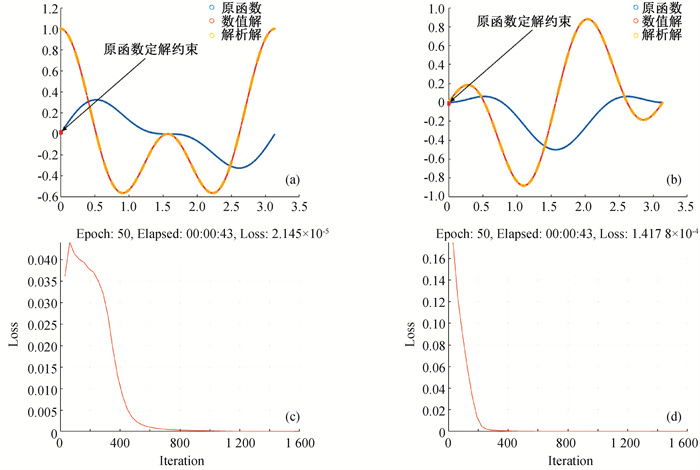
Fig.4 Numerical results of degenerate kernel Fredholm equation (a) distribution scatter diagram of the original function of integral item 1 and numerical solution of equation; (b) distribution scatter diagram of the original function of integral item 2 and numerical solution of equation; (c) Fall-Loss-1 trend graph with time (first 50 times); (d) Fall-Loss-2 trend graph with time (first 50 times)

Table 4 Loss function, sample generation method and numerical operation results of linear Volterra-Fredholm equation

损失函数来源	约束形式	样本数量	样本生成方式	损失函数权重	σ_MSE/10^-8	σ_{MSE, max}/10^-6	Loss/10^-8
控制方程F_f-loss－1；F_f-loss－2	方程(17)、(18)	1 000	随机分布	1	6.503 8(图 5(a))	4.307 3(图 5(a))	1.965 1(图 5(a))
原函数定解约束F_d－loss－1；F_d－loss－2	t₁=0, F₀₁(0)=0;t₂=0, F₀₂(0)=0	1	固定	30	9.735 7(图 5(b))	5.995 4(图 5(b))	2.510 0(图 5(b))

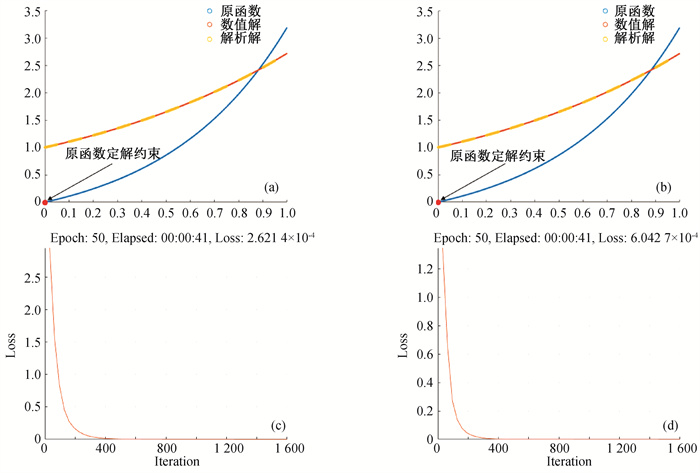
Fig.5 Numerical results of the linear Volterra-Fredholm equation (a) distribution scatter diagram of the original function of integral item 1 and numerical solution of equation; (b) distribution scatter diagram of the original function of integral item 2 and numerical solution of equation; (c) Fall-loss-1 trend graph with time (first 50 times); (d) Fall-loss-2 trend graph with time (first 50 times)

Table 5 Loss function, sample generation method and numerical operation results of delay equation

损失函数来源	约束形式	样本数量	样本生成方式	损失函数权重	σ_MSE/10^-8	σ_{MSE, max}/10^-6	Loss/10^-8
控制方程F_f－loss－1；F_f－loss－2	方程(17)、(18)	1000	随机分布	1	8.348 3(图 6(a))	2.439 4(图 6(a))	3.008 5(图 6(a))
原函数定解约束F_d－loss－1；F_d－loss－2	t₁=0, F₀₁(0)=0;t₂=0, F₀₂(0)=0	1	固定	30	7.214 4(图 6(b))	2.154 8(图 6(b))	2.747 2(图 6(b))

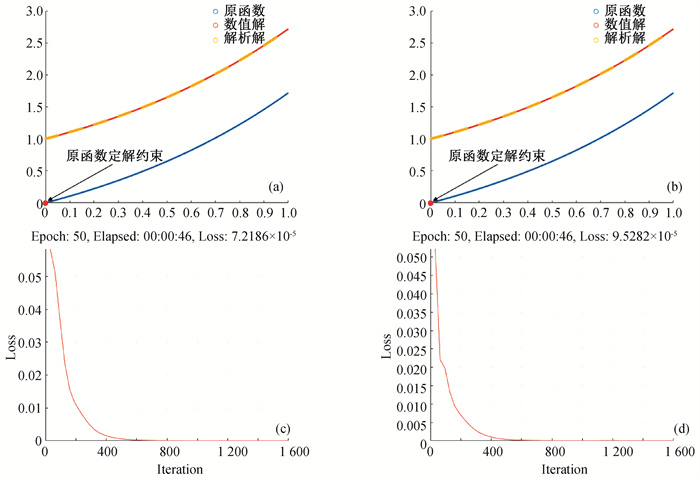
Fig.6 Numerical results of time-delay equation (a) distribution scatter diagram of the original function of integral item 1 and numerical solution of equation; (b) distribution scatter diagram of the original function of integral item 2 and numerical solution of equation; (c) Fall-Loss-1 trend graph with time (first 50 times); (d)Fall-Loss-2 trend graph with time (first 50 times)

References 22

1	颜子翔, 康炜, 张维岩, 等. 温稠密物质状态方程的路径积分蒙特卡罗方法研究进展[J]. 计算物理, 2023, 40 (2): 258- 274.
2	李志勇. 基于二维广义横向积分综合一维半解析的三维中子扩散节块法[J]. 计算物理, 2022, 39 (2): 153- 158.
3	李星. 积分方程[M]. 北京: 科学出版社, 2008.
4	吕涛, 黄晋. 积分方程的高精度算法[M]. 北京: 科学出版社, 2013.
5	张庆福, 姚军, 黄朝琴, 等. 裂缝性介质多尺度深度学习模型[J]. 计算物理, 2019, 36 (6): 665- 672.
6	HUANG Shudong, FENG Wentao, TANG Chenwei, et al. Partial differential equations meet deep neural networks: A survey[EB/OL]. (2022-10-27). https://arxiv.org/abs/2211.05567.
7	RAISSI M , PERDIKARIS P , KARNIADAKIS G E . Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378, 686- 707. DOI
8	GUAN Yu , FANG Tingting , ZHANG Diankun , et al. Solving fredholm integral equations using deep learning[J]. International Journal of Applied and Computational Mathematics, 2022, 8 (2): 87. DOI
9	张殿焜. 基于Tensorflow的神经网络求解Fredholm积分方程[D]. 杭州: 浙江理工大学, 2020.
10	GUO Rui , SHAN Tao , SONG Xiaoqian , et al. Physics embedded deep neural network for solving volume integral equation: 2-D case[J]. IEEE Transactions on Antennas and Propagation, 2022, 70 (8): 6135- 6147. DOI
11	SUN Jia , LIU Yinghua , WANG Yizheng , et al. BINN: A deep learning approach for computational mechanics problems based on boundary integral equations[J]. Computer Methods in Applied Mechanics and Engineering, 2023, 410, 116012. DOI
12	华东师范大学数学系. 数学分析-下册[M]. 3版北京: 高等教育出版社, 2001.
13	刘东, 罗琦, 唐雷, 等. 基于PINN深度机器学习技术求解多维中子学扩散方程[J]. 核动力工程, 2022, 43 (2): 1- 8.
14	HAGAN M T , DEMUTH H B , BEALE M H , et al. Neural network design[M]. 2nd ed. Stillwater: Martin Hagan, 2014.
15	PANG Guogfei , LU Lu , KARNIADAKIS G E . fPINNs: Fractional physics-informed neural networks[J]. SIAM Journal on Scientific Computing, 2019, 41 (4): A2603- A2626. DOI
16	JAGTAP A D , KARNIADAKIS G E . Extended physics-informed neural networks (XPINNs): A generalized space-time domain decomposition based deep learning framework for nonlinear partial differential equations[J]. Communications in Computational Physics, 2020, 28 (5): 2002- 2041. DOI
17	KHARAZMI E , ZHANG Zhongqiang , KARNIADAKIS G E M . hp-VPINNs: Variational physics-informed neural networks with domain decomposition[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 374, 113547. DOI
18	BAYDIN A G , PEARLMUTTER B A , RADUL A A , et al. Automatic differentiation in machine learning: A survey[J]. The Journal of Machine Learning Research, 2017, 18 (1): 5595- 5637.
19	YANG Liu , MENG Xuhui , KARNIADAKIS G E . B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data[J]. Journal of Computational Physics, 2021, 425, 109913.
20	LU Lu , MENG Xuhui , MAO Zhiping . DeepXDE: A deep learning library for solving differential equations[J]. SIAM Review, 2021, 63 (1): 208- 228.
21	MCCLENNY L D , BRAGA-NETO U M . Self-adaptive physics-informed neural networks[J]. Journal of Computational Physics, 2023, 474, 111722.
22	ZHU Shiqiang , YU Ting , XU Tao , et al. Intelligent computing: The latest advances, challenges, and future[J]. Intelligent Computing, 2023, 2, 0006.

[1]	Xiao-bo WANG, Jun-ping YIN, Yan XU. Robust Loss Functions for Signal Modulation Recognition with Noise Labels [J]. Chinese Journal of Computational Physics, 2022, 39(4): 386-394.
[2]	Yingdong LU, Duqu WEI. Power System Chaos Prediction Based on DLSTM with Genetic Attention Mechanism [J]. Chinese Journal of Computational Physics, 2022, 39(3): 371-378.
[3]	ZHANG Qingfu, YAO Jun, HUANG Zhaoqin, LI Yang, WANG Yueying. A Multiscale Deep Learning Model for Fractured Porous Media [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2019, 36(6): 665-672.
[4]	Zhang Yerong, Nie Zaiping, Qi Lanfen, Zhang Tiyuan. INVERSION OF THE CONDUCTIVITY IN THE LARGE FORMATION REGION USING THE MULTI INFORMATION OF ARRAY [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 1998, 15(3): 321-330.