Modeling and Analysis Methods for Complex Fields Based on Phase Space

doi:10.19596/j.cnki.1001-246x.8379

Abstract

Abstract:

We review two modeling and analysis methods based on phase space and their applications. The first is Minkowski functionals-based Morphological Analysis Method (Min-MAM), and the second is Discrete Boltzmann modeling and analysis Method (DBM). Both of them are developed from phase space description in statistical physics. Based on independent behavior characteristic quantities, a phase space is constructed, and the phase space and its subspaces are used to describe behavior characteristics of a system. A given point in the phase space corresponds to a set of behavior characteristics of the system. The distance d between two points is used to describe the difference of two groups of behavioral characteristics, and its reciprocal, S=1/d, is used to describe similarity of two groups of behavioral characteristics. Mean value of the distance between two points over a period of time, ${\bar d}$, is used to describe difference between two kinetic processes, and its reciprocal, S_p=1/${\bar d}$, is used to describe similarity of two kinetic processes, Historically, Min-MAM appeared earlier. Receiving its inspiration is the key step in the development of discrete Boltzmann method towards phase space description method. Min-MAM is independent of data sources, so results obtained with discrete Boltzmann simulation can be further understood on another level or perspective by using Min-MAM, in addition to its own analysis functions. In the study of complex media kinetics, these two methods, from different perspectives, provide information that can be stratified and studied quantitatively.

Key words: discrete Boltzmann method, morphological analysis method, complex fields, statistical physics, phase space

CLC Number:

O359

Aiguo XU, Jiahui SONG, Feng CHEN, Kan XIE, Yangjun YING. Modeling and Analysis Methods for Complex Fields Based on Phase Space[J]. Chinese Journal of Computational Physics, 2021, 38(6): 631-660.

Figures/Tables 38

Fig.1 A schematic of temperature field in a two-dimensional system

Fig.2 A schematic of morphological analysis of a two-dimensional temperature field

Fig.3 (a)Morphological phase space A-L-χ; (b)Morphological difference (or similarity); (c)Process difference (or similarity)

Fig.4 A set of configurations with temperature contour in the shock loading and unloading procedure (a) t=500 ns; (b) t=750 ns; (c) t=850 ns; (d) t=1100 ns

Fig.5 Morphological analysis for the procedure of shock wave action on porous material

Fig.6 Morphological analysis in the A-L-χ space

Fig.7 Process similarity versus temperature threshold (a) DT=120; (b) DT=300

Fig.8 Three similar pattern dynamical procedures in A-L-χ space

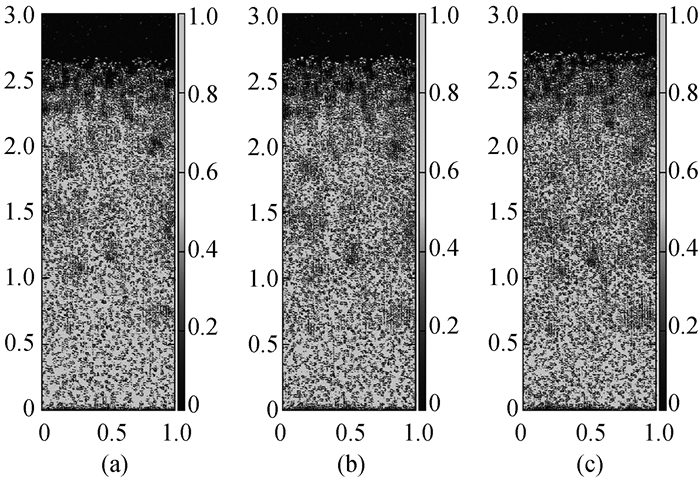
Fig.9 Condensed temperature patterns at 500 ns in three similar dynamical procedures (a) V=1000 m ·s-1, DT=92 K; (b) V=1100 m ·s-1, DT=120 K; (c) V=1200 m ·s-1, DT=154 K

Fig.10 Temperature threshold versus shock strength (a) Δ=0.077; (b) Δ=0.46

Fig.11 Temperature threshold versus porosity

Fig.12 A set of configurations with pressure contours in shock loading and unloading procedure (Δ=0.46, V=1300 m ·s-1)

Fig.13 Morphological analysis for the procedure of shock wave action on porous material

Fig.14 Minkowski description in A-L-χ space

Fig.15 Process similarity versus Pth2 for cases with different shock strengths and same porosity

Fig.16 Two pairs of procedures showing similarity

Fig.17 Pressure threshold versus shocking strength for similar procedures

Fig.18 Pth2(Δ2) versus Pth1 under same shock strength

Fig.19 Pressure threshold versus porosity for similar procedures

Fig.20 A schematic for development of two description methods based on phase space

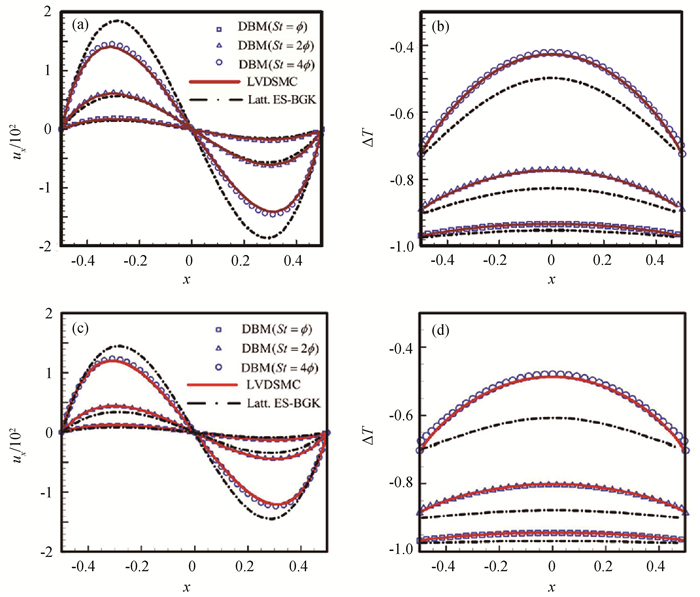
Fig.21 At Kn=0.5, (a) velocity perturbations for a BGK gas; (b) temperature perturbations for a BGK gas; (c) velocity perturbations for a hard-sphere gas; (d) temperature perturbations for a hard-sphere gas[55]

Fig.22 Cavity flow in steady state at Kn =0.075

Fig.23 Comparison of DBM viscous stress and NS viscous stress

Fig.24 A schematic of Minkowski morphological quantity, SD stage duration at different heat transfer coefficients and average heat flux

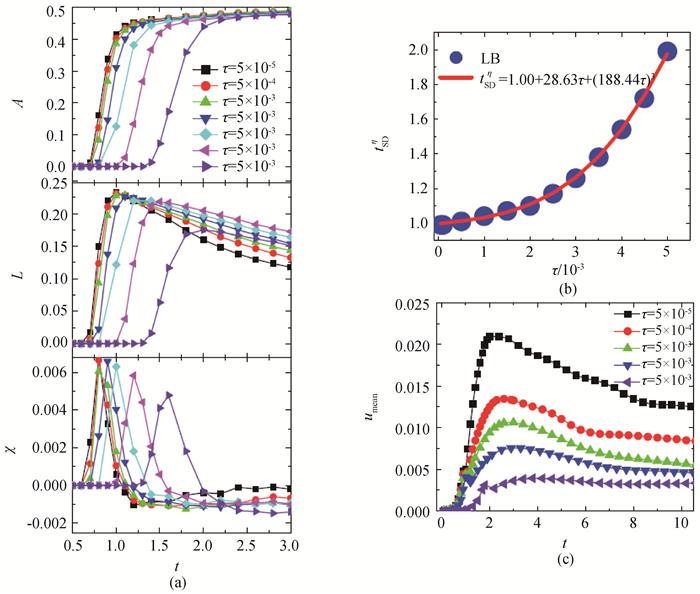
Fig.25 A schematic of Minkowski morphological quantity, SD stage duration at different relaxation time (viscosity coefficient) and local average speed

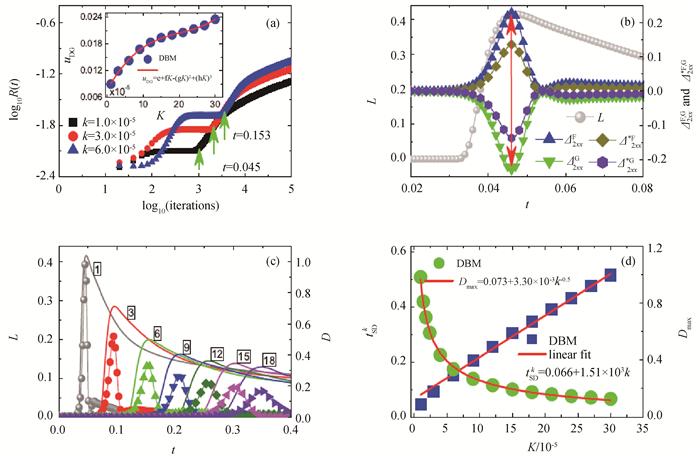
Fig.26 (a) Evolutions of the characteristic domain sizes R; (b) Evolutions of the boundary length L and the xx component of some TNE manifestations; (c) Evolutions of the boundary lengths L (solid curves) and the corresponding TNE intensities D (curves with solid symbols) in phase separation processes with various K; (d) Duration of the spinodal decomposition stage tSD and the maximum TNE intensity Dmax as functions of K

Fig.27 Four kinds of criterions to discriminate the stages of the spinodal decomposition and domain growth

Fig.28 Profiles of characteristic domain sizes and rates of entropy production at different Prandtl numbers (heat conduction coefficient)

Fig.29 Profiles of critical time tSD and the maximum entropy production rates as functions of heat conductivity

Fig.30 Profiles of characteristic domain sizes and rates of entropy production at different viscosity coefficients

Fig.31 Profiles of critical time tSD and amplitudes of entropy production rates as functions of viscosity coefficient

Fig.32 Profiles of characteristic domain sizes and rates of entropy production at different coefficients of surface tension

Fig.33 Profiles of duration time of the SD stage (tSD) and amplitudes of entropy production rates as functions of coefficient of surface tension

Fig.34 Relations between two kinds of entropy production rate amplitude

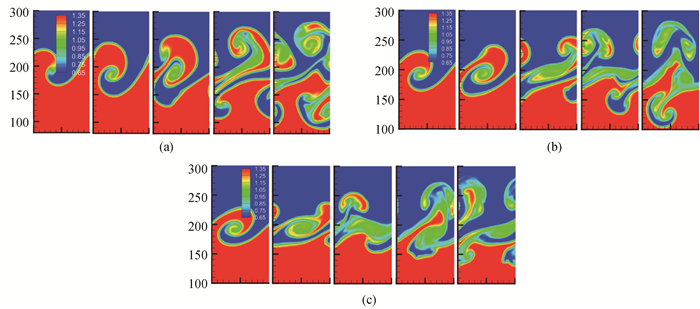
Fig.35 Temperature distributions of coupled RTKHI (a) g=0.005, u0=0.05; (b)g=0.005, u0=0.1; (c) g=0.005, u0=0.15 (Images from left to right correspond to t=100, 150, 200, 250, 300, respectively.)

Fig.36 Perturbation amplitude A, growth rate dA/dt, and morphological boundary length L vs time t

Fig.37 Morphological analysis of main mechanism in the early stage of an RTKHI system

Fig.38 Applications of non-equilibrium characteristics in the early main mechanism judgment (a)- (d) and transition point capture(e)- (f)

References 89

1	陈式刚. 非平衡统计力学[M]. 北京: 科学出版社, 2010.
2	沈惠川. 统计力学[M]. 合肥: 中国科学技术大学出版社, 2011.
3	SERRA J. Image analysis and mathematical morphology[M]. New York: Academic, Vols(1/2), 1982.
4	MECKE K R. Morphological characterization of patterns in reaction-diffusion systems[J]. Phys Rev E, 1996, 53, 4794. DOI
5	AKSIMENTIEV A, MOORTHI K, HOLYST R. Scaling properties of the morphological measures at the early and intermediate stages of the spinodal decomposition in homopolymer blends[J]. J Chem Phys, 2000, 112, 1. DOI
6	MECKE K R, SOFONEA V. Morphology of spinodal decomposition[J]. Phys Rev E, 1997, 56, R3761- R3764. DOI
7	GÒŹDŹ W, HOŁYST R. High genus periodic gyroid surfaces of nonpositive Gaussian curvature[J]. Physical Review Letters, 1996, 76 (15): 2726. DOI
8	XU A, ZHANG G, YING Y, et al. Shock wave response of porous materials: From plasticity to elasticity[J]. Phys Scr, 2010, 81, 055805. DOI
9	XU A, ZHANG G, LI H, et al. Comparison study on characteristic regimes in shocked porous materials[J]. Chinese Phys Lett, 2010, 27 (2): 026201. DOI
10	XU A, ZHANG G, LI H, et al. Dynamical similarity in shock wave response of porous material: From the view of pressure[J]. Comput Math Appl, 2011, 61, 3618. DOI
11	XU A, ZHANG G, LI H, et al. Temperature pattern dynamics in shocked porous materials[J]. Sci China: Phys Mech Astron, 2010, 53 (8): 1466- 1474. DOI
12	GAN Y, XU A, ZHANG G, et al. Phase separation in thermal systems: A lattice Boltzmann study and morphological characterization[J]. Physical Review E, 2011, 84 (4): 046715. DOI
13	GAN Yanbiao, XU Aiguo, ZHANG Guangcai, et al. Lattice Boltzmann study of thermal phase separation: Effects of heat conduction, viscosity and Prandtl number[J]. Europhysics Letters, 2012, 97 (4): 44002. DOI
14	ZHANG Yudong, XU Aiguo, ZHANG Guangcai, et al. Entropy production in thermal phase separation: A kinetic-theory approach[J]. Soft Matter, 2019, 15 (10): 2245- 2259. DOI
15	CHEN Feng, XU Aiguo, ZHANG Yudong, et al. Morphological and non-equilibrium analysis of coupled Rayleigh-Taylor-Kelvin-Helmholtz instability[J]. Physics of Fluids, 2020, 32, 104111. DOI
16	XU Aiguo, ZHANG Guangcai, YING Yangjun, et al. Complex fields in heterogeneous materials under shock: Modeling, simulation and analysis[J]. Science China: Physics, Mechanics & Astronomy, 2016, 59, 650501.
17	XU Aiguo, ZHANG Guangcai, PAN X, et al. Morphological characterization of shocked porous material[J]. Journal of Physics D: Applied Physics, 2009, 42 (7): 075409. DOI
18	XU Aiguo, ZHANG Guangcai, ZHANG Ping, et al. Dynamics and thermodynamics of porous HMX-like material under shock[J]. Communications in Theoretical Physics, 2009, 52 (5): 901. DOI
19	许爱国, 张广财, 蔚喜军, 等. 冲击作用下多孔材料热力学特征的模拟与分析[J]. 中国工程科学, 2009, 11 (9): 13- 19. DOI
20	GAN Yanbiao, XU Aiguo, ZHANG Guangcai, et al. Discrete Boltzmann modeling of multiphase flows: Hydrodynamic and thermodynamic non-equilibrium effects[J]. Soft Matter, 2015, 11 (26): 5336- 5345. DOI
21	XU Aiguo, ZHANG Guangcai, GAN Yanbiao, et al. Lattice Boltzmann modeling and simulation of compressible flows[J]. Frontiers of Physics, 2012, 7 (5): 582- 600. DOI
22	CAGIN T, PETTITT B M. Grand molecular dynamics: A method for open systems[J]. Molecular Simulation, 1991, 6 (1-3): 5- 26. DOI
23	WU L, WHITE C, SCANLON T J, et al. Deterministic numerical solutions of the Boltzmann equation using the fast spectral method[J]. Journal of Computational Physics, 2013, 250, 27- 52. DOI
24	BIRD G A. Recent advances and current challenges for DSMC[J]. Computers & Mathematics with Applications, 1998, 35 (1-2): 1- 14.
25	GRAD H. On the kinetic theory of rarefied gases[J]. Communications on Pure and Applied Mathematics, 1949, 2 (4): 331- 407. DOI
26	刘畅, 徐昆. 离散时空直接建模思想及其在模拟多尺度输运中的应用[J]. 空气动力学学报, 2020, 38 (2): 197- 216.
27	SUCCI S. The lattice Boltzmann equation: For complex states of flowing matter[M]. Oxford University Press, 2018.
28	郭照立, 郑楚光. 格子Boltzmann方法的原理及应用[M]. 北京: 科学出版社, 2009.
29	HE Y L, WANG Y, LI Q. Lattice Boltzmann method: Theory and applications[M]. Beijing: Science Press, 2009.
30	HUANG H, SUKOP M C, LU X. Multiphase lattice Boltzmann methods: Theory and application[M]. Wiley, 2015.
31	LIANG H, HU X, HUANG X, et al. Direct numerical simulations of multi-mode immiscible Rayleigh-Taylor instability with high Reynolds numbers[J]. Physics of Fluids, 2019, 31 (11): 112104. DOI
32	SUN D. A discrete kinetic scheme to model anisotropic liquid-solid phase transitions[J]. Applied Mathematics Letters, 2020, 103, 106222. DOI
33	QIAN Y H, D'HUMIÈRES D, LALLEMAND P. Lattice BGK models for Navier-Stokes equation[J]. Europhysics Letters, 1992, 17 (6): 479. DOI
34	SHAN X, CHEN H. Lattice Boltzmann model for simulating flows with multiple phases and components[J]. Physical Review E, 1993, 47 (3): 1815. DOI
35	CHEN S, CHEN H, MARTNEZ D, et al. Lattice Boltzmann model for simulation of magnetohydrodynamics[J]. Physical Review Letters, 1991, 67 (27): 3776. DOI
36	CHAI Z, SHI B. Multiple-relaxation-time lattice Boltzmann method for the Navier-Stokes and nonlinear convection-diffusion equations: Modeling, analysis, and elements[J]. Physical Review E, 2020, 102 (2): 023306.
37	DU R, SUN D, SHI B, et al. Lattice Boltzmann model for time sub-diffusion equation in Caputo sense[J]. Applied Mathematics and Computation, 2019, 358, 80- 90. DOI
38	XING H, DONG X, SUN D, et al. Anisotropic lattice Boltzmann-phase-field modeling of crystal growth with melt convection induced by solid-liquid density change[J]. Journal of Materials Science & Technology, 2020, 57, 26- 32.
39	ZHAN C, CHAI Z, SHI B. A lattice Boltzmann model for the coupled cross-diffusion-fluid system[J]. Applied Mathematics Letters, 2021, 400, 126105.
40	LI Xindong, ZHAO Yingkui, HU Zongmin, et al. Investigation of normal shock structure by using Navier-Stokes equations with the second viscosity[J]. Chinese Journal of Computational Physics, 2020, 37 (5): 505- 513.
41	LI Xiao, SUN Chen, SHEN Zhijun. Numerical simulation of one-dimensional elastic-perfectly plastic flow and suppression of wall heating phenomenon[J]. Chinese Journal of Computational Physics, 2020, 37 (5): 539- 550.
42	SUN Chen, LI Xiao, SHEN Zhijun. A Godunov method with staggered Lagrangian discretization applicable to isentropic flows[J]. Chinese Journal of Computational Physics, 2020, 37 (5): 529- 538.
43	ZHAO Fei, SHENG Zhiqiang, YUAN Guangwei. A positivity-preserving finite volume scheme based on second-order scheme[J]. Chinese Journal of Computational Physics, 2020, 37 (4): 379- 392.
44	KARBALAEI A, KUMAR R, CHO H J. Thermocapillarity in microfluidics-A review[J]. Micromachines, 2016, 7 (1): 13. DOI
45	许爱国, 张广财, 应阳君. 燃烧系统的离散Boltzmann建模与模拟研究进展[J]. 物理学报, 2015, 64, 184701. DOI
46	XU Aiguo, ZHANG Guangcai, ZHANG Yudong. Discrete Boltzmann modeling of compressible flows[M]//KYZAS G Z, MITROPOULOS A C, eds. Kinetic Theory, Chap 02. Rijeka: InTech, 2018.
47	许爱国, 张广财, 甘延标. 相分离过程的离散Boltzmann方法研究进展[J]. 力学与实践, 2016, 38 (4): 361- 374.
48	许爱国, 陈杰, 宋家辉, 等. 多相流系统的离散玻尔兹曼研究进展[J]. 空气动力学学报, 2021, 39 (3): 1- 32.
49	XU Aiguo, LIN Chuangdong, ZHANG Guangcai, et al. Multiple-relaxation-time lattice Boltzmann kinetic model for combustion[J]. Physical Review E, 2015, 91 (4): 043306. DOI
50	MCNAMARA G R, ZANETTI G. Use of the Boltzmann equation to simulate lattice automata[J]. Phys Rev Lett, 1988, 61, 2332. DOI
51	MANELA A, HADJICONSTANTINOU N G. Gas-flow animation by unsteady heating in a microchannel[J]. Physics of Fluids, 2010, 22 (6): 062001. DOI
52	HOMOLLE T M M, HADJICONSTANTINOU N G. Low-variance deviational simulation Monte Carlo[J]. Physics of Fluids, 2007, 19 (4): 041701. DOI
53	HOMOLLE T M M, HADJICONSTANTINOU N G. A low-variance deviational simulation Monte Carlo for the Boltzmann equation[J]. Journal of Computational Physics, 2007, 226 (2): 2341- 2358. DOI
54	RADTKE G A, HADJICONSTANTINOU N G, WAGNER W. Low-noise Monte Carlo simulation of the variable hard sphere gas[J]. Physics of Fluids, 2011, 23 (3): 030606. DOI
55	ZHANG Y, XU A, ZHANG G, et al. Discrete Boltzmann method for non-equilibrium flows: Based on Shakhov model[J]. Computer Physics Communications, 2019, 238, 50- 65. DOI
56	SHANKAR P N, DESHPANDE M D. Fluid mechanics in the driven cavity[J]. Annual Review of Fluid Mechanics, 2000, 32 (1): 93- 136. DOI
57	JOHN B, GU X J, EMERSON D R. Effects of incomplete surface accommodation on non-equilibrium heat transfer in cavity flow: A parallel DSMC study[J]. Computers & Fluids, 2011, 45 (1): 197- 201.
58	HUANG J C, XU K, YU P. A unified gas-kinetic scheme for continuum and rarefied flows Ⅱ: Multi-dimensional cases[J]. Communications in Computational Physics, 2012, 12 (3): 662- 690. DOI
59	GAN Y, XU A, ZHANG G, et al. Discrete Boltzmann trans-scale modeling of high-speed compressible flows[J]. Physical Review E, 2018, 97 (5): 053312. DOI
60	YE X Y, LIN F W, HUANG X J, et al. Polymer fibers with hierarchically porous structure: Combination of high temperature electrospinning and thermally induced phase separation[J]. Rsc Advances, 2013, 3 (33): 13851- 13858. DOI
61	YEGANEH J K, GOHARPEY F, FOUDAZI R. Anomalous phase separation behavior in dynamically asymmetric LCST polymer blends[J]. RSC Advances, 2014, 4 (25): 12809- 12825. DOI
62	CORBERI F, GONNELLA G, LAMURA A. Spinodal decomposition of binary mixtures in uniform shear flow[J]. Physical Review Letters, 1998, 81 (18): 3852. DOI
63	XU A, GONNELLA G, LAMURA A. Phase-separating binary fluids under oscillatory shear[J]. Physical Review E, 2003, 67 (5): 056105. DOI
64	VERBERG R, POOLEY C M, YEOMANS J M, et al. Pattern formation in binary fluids confined between rough, chemically heterogeneous surfaces[J]. Physical Review Letters, 2004, 93 (18): 184501. DOI
65	POOLEY C M, YEOMANS J M. Stripe formation in differentially forced binary systems[J]. Physical Review Letters, 2004, 93 (11): 118001. DOI
66	MARENDUZZO D, ORLANDINI E, YEOMANS J M. Permeative flows in cholesteric liquid crystals[J]. Physical Review Letters, 2004, 92 (18): 188301. DOI
67	XU A, GONNELLA G, LAMURA A. Morphologies and flow patterns in quenching of lamellar systems with shear[J]. Physical Review E, 2006, 74 (1): 011505. DOI
68	GONNELLA G, LAMURA A, SOFONEA V. Lattice Boltzmann simulation of thermal nonideal fluids[J]. Physical Review E, 2007, 76 (3): 036703. DOI
69	ZHANG Y D, XU A G, QIU J J, et al. Kinetic modeling of multiphase flow based on simplified Enskog equation[J]. Frontiers of Physics, 2020, 15 (6): 1- 13.
70	CRISTINI V, TAN Y C. Theory and numerical simulation of droplet dynamics in complex flows-a review[J]. Lab on a Chip, 2004, 4 (4): 257- 264. DOI
71	TEZDUYAR T E. Interface-tracking and interface-capturing techniques for finite element computation of moving boundaries and interfaces[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195 (23-24): 2983- 3000. DOI
72	SZEWC K, POZORSKI J, MINIER J P. Simulations of single bubbles rising through viscous liquids using smoothed particle hydrodynamics[J]. International Journal of Multiphase Flow, 2013, 50, 98- 105. DOI
73	赵明娟, 邓志成, 赵龙志. 激光熔注中增强相颗粒对晶粒生长影响的CA模拟[J]. 功能材料, 2015, 46 (1): 6.
74	DU L F, ZHANG R, ZHANG L M. Phase-field simulation of dendritic growth in a forced liquid metal flow coupling with boundary heat flux[J]. Science China Technological Sciences, 2013, 56 (10): 2586- 2593. DOI
75	JACQMIN D. Calculation of two-phase Navier-Stokes flows using phase-field modeling[J]. Journal of Computational Physics, 1999, 155 (1): 96- 127. DOI
76	XU A, GONNELLA G, LAMURA A. Numerical study of the ordering properties of lamellar phase[J]. Physica A: Statistical Mechanics and Its Applications, 2004, 344 (3-4): 750- 756. DOI
77	XU A, GONNELLA G, LAMURA A. Simulations of complex fluids by mixed lattice Boltzmann-finite difference methods[J]. Physica A: Statistical Mechanics and Its Applications, 2006, 362 (1): 42- 47. DOI
78	XU A, GONNELLA G, LAMURA A, et al. Scaling and hydrodynamic effects in lamellar ordering[J]. EPL (Europhysics Letters), 2005, 71 (4): 651- 651. DOI
79	ZHOU Y. Rayleigh-Taylor and Richtmyer-Meshkov instability induced flow, turbulence, and mixing Ⅰ[J]. Physics Reports, 2017, 720-722, 1- 136. DOI
80	ZHOU Y. Rayleigh-Taylor and Richtmyer-Meshkov instability induced flow, turbulence, and mixing Ⅱ[J]. Physics Reports, 2017, 723-725, 1- 160. DOI
81	廖深飞, 邹立勇, 黄熙龙, 等. Richtmyer-Meshkov不稳定的双椭圆气柱相互作用的PIV研究[J]. 中国科学: 物理学力学天文学, 2016, 46, 034702.
82	DING J, SI T J, YANG J, et al. Shock tube experiments on converging Richtmyer-Meshkov instability[J]. Physical Review Letters, 2017, 119, 014501. DOI
83	HUANG S, XU J, LUO Y, et al. Smoothed particle hydrodynamics simulation of converging Richtmyer-Meshkov instability[J]. Physics of Fluids, 2020, 32, 086102. DOI
84	WANG Z, XUE K, HAN P. Bell-Plesset effects on Rayleigh-Taylor instability at cylindrically divergent interfaces between viscous fluids[J]. Physics of Fluids, 2021, 33 (3): 034118. DOI
85	LAI H, XU A, ZHANG G, et al. Nonequilibrium thermohydrodynamic effects on the Rayleigh-Taylor instability in compressible flows[J]. Physical Review E, 2016, 94 (2): 023106. DOI
86	CHEN F, XU A G, ZHANG G C. Viscosity, heat conductivity, and Prandtl number effects in the Rayleigh-Taylor instability[J]. Frontiers of Physics, 2016, 11 (6): 1- 14.
87	LIN C, XU A, ZHANG G, et al. Discrete Boltzmann modeling of Rayleigh-Taylor instability in two-component compressible flows[J]. Physical Review E, 2017, 96 (5): 053305. DOI
88	YE H, LAI H, LI D, et al. Knudsen number effects on two-dimensional Rayleigh-Taylor instability in compressible fluid: Based on a discrete Boltzmann method[J]. Entropy, 2020, 22 (5): 500. DOI
89	CHEN F, XU A, ZHANG G. Collaboration and competition between Richtmyer-Meshkov instability and Rayleigh-Taylor instability[J]. Physics of Fluids, 2018, 30 (10): 102105. DOI

[1]	HUA Wei, LV Yan, LIU Shixing, LIU Xueshen. Dynamic Study of Cubic-Quintic Nonlinear Schrödinger Equation and Pattern Drifting [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2017, 34(4): 495-504.
[2]	LIU Xue-shen, HUA Wei, DING Pei-zhu. Dynamic Properties of Nonlinear Schrödinger Equation [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2004, 21(6): 495-500.
[3]	YOU Rong-yi, CHEN Zhong. Calculation of the Approximate Entropy and the Information Entropy of EEG in Phase Space [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2004, 21(4): 341-344.
[4]	Hongdong Zhang, Jianming Lu, Yuliang Yang. STOCHASTIC BOUNDARY CONDITIONS OF MONTE CARLO STATISTICAL PHYSICS [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 1992, 9(2): 197-202.