Effects of Conduction Block and Reentry on Evolution of Spiral Waves

doi:10.19596/j.cnki.1001-246x.8552

Abstract

Abstract:

We study conduction block and reentry induced by conduction velocity restitution, and their effects on the evolution of spiral waves. Simulation shows that the shape of stable spiral waves, Eckhaus instability and Doppler instability of spiral waves are associated with conduction block and reentry. The stable spiral wave exhibits concave or rhombic shape as the conduction block reduces its symmetry. The Eckhaus instability of spiral waves emerges as serious conduction blocks and the accompanying reentry initiated far from the spiral wave tip. In the case that serious conduction blocks begin near the spiral wave tip, the spiral wave meanders, and then the wave arms near the tip compress in one direction but elongate in other direction, which lead to the Doppler instability of spiral waves. This work tries to expound mechanisms of the evolution of spiral waves in the sight of cellular and electrical level.

Key words: conduction velocity restitution, conduction block, reentrant, spiral waves, cellular automata

Chengqian LI, Furong GUAN, Minyi DENG. Effects of Conduction Block and Reentry on Evolution of Spiral Waves[J]. Chinese Journal of Computational Physics, 2023, 40(1): 117-126.

Figures/Tables 10

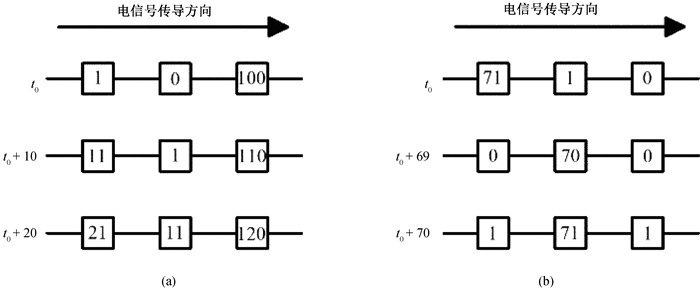
Fig.1 Examples of the emergence of (a) conduction block and (b) reentry (The square frames and the figures represent cells and their state values, respectively.)

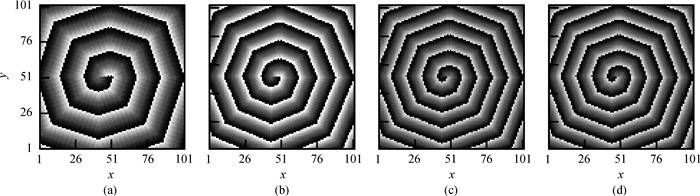
Fig.2 Patterns of stable spiral waves without CVR at t=30 000 and γ=2 (a)α=2 300, β=34;(b)α=1 400, β=40; (c)α=1 500, β=40; (d)α=2 600, β=36(The white, dark and gray represent the state of rest, excited and refractory, respectively. Deeper gray indicates smaller value of refractory state.)

Fig.3 The concave shape of spiral wave due to CVR and its relation with conduction block (a)~(c)spiral wave patterns; (d)~(f)local state distributions in concave region; (g)~(i)local state distributions in non-concave region (The square frames and figures in local state distributions are the same as in Fig. 1. Colors in patters represent the same as in Fig. 2. The cell with attention is signed with a circle. The end of arrow is at the point where electrical signal arrives, and beginning of the arrow is the source of electrical signal. Parameters are the same as in Fig. 2(a).)

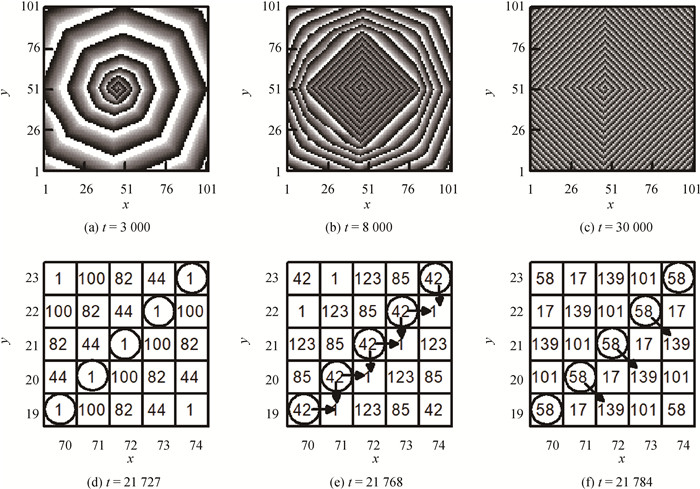
Fig.4 Rhombic shape of spiral wave due to CVR and its relation with conduction block (a)~(c)spiral wave patterns; (d)~(f) local state distributions reflecting conduction blocks along the diagonal direction (Colors in patterns and signals in state distributions represent the same as in Fig. 3. Parameters are the same as in Fig. 2(b).)

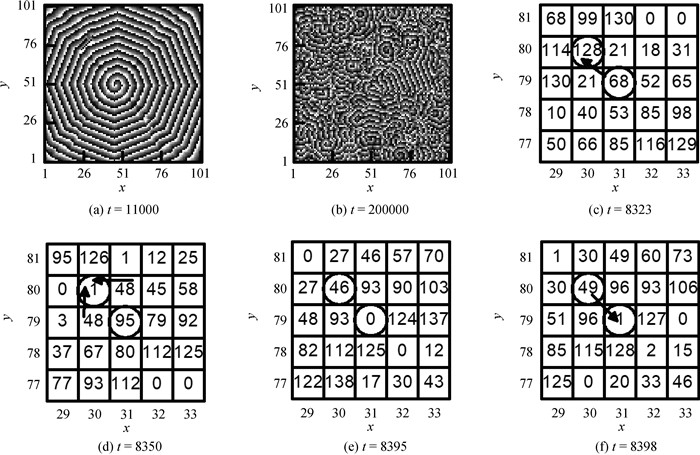
Fig.5 Eckhaus instability due to CVR and its relation with conduction block and reentry (a) and (b) patterns during Eckhaus instability process; (c) and (d) local state distributions reflecting the conduction block; (e) and (f) local state distributions reflecting the reentry (Colors in patters and signals in state distributions represent the same as in Fig. 3. Parameters are the same as in Fig. 2(c).)

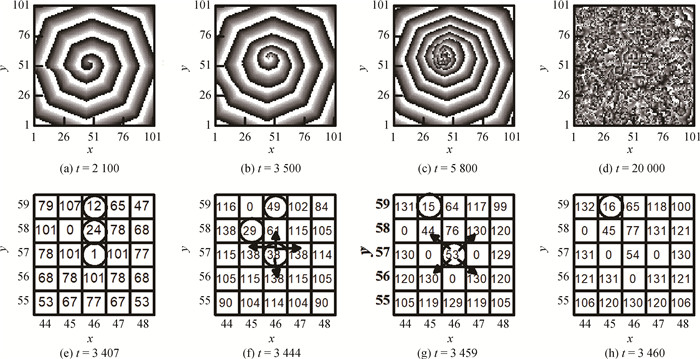
Fig.6 Doppler instability due to CVR and its relation with conduction block (a)~(d)patterns during Doppler instability process; (e)~(h)local state distributions reflecting the conduction block (Colors in patter and signals in state distributions represent the same as in Fig. 3. Parameters are the same as in Fig. 2(d).)

Table 1 Conduction time of a pulse from a cell at (69, 77) in Fig. 3 and excitation situation of its neighbors

单位距离传导时间	激发正向邻居	激发斜向邻居
40	失败	成功
35	成功	失败
37	成功	失败
24	失败	失败
21	失败	失败
21	失败	成功

Table 2 Conduction time of a pulse from a cell at (46, 84) in Fig. 3 and excitation situation of its neighbors

单位距离传导时间	激发正向邻居	激发斜向邻居
27	成功	成功
27	成功	成功
29	成功	失败
30	成功	失败
30	成功	失败
28	成功	成功

Table 3 Conduction time of a pulse from a cell at (75, 71) in Fig. 4 and excitation situation of its neighbors

单位距离传导时间	激发正向邻居	激发斜向邻居
24	失败	失败
45	成功	成功
41	成功	失败
43	成功	失败
38	成功	失败

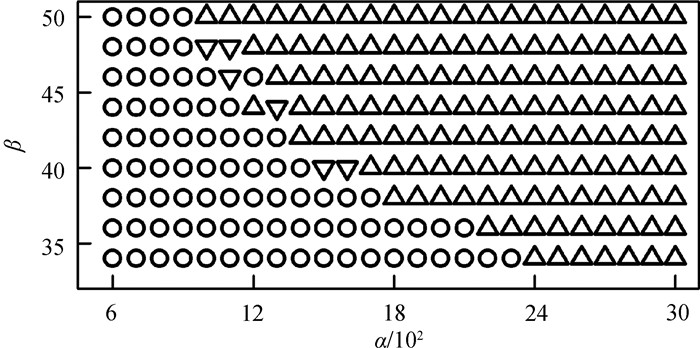
Fig.7 Evolution types of spiral waves under different parameters as CVR is considered (〇, ▽and △ represent stable spiral waves, Eckhaus instability and Doppler instability, respectively.)

References 23

1	ROTERMUND H H , ENGEL W , KORDESCH M , et al. Imaging of spatio-temporal pattern evolution during carbon monoxide oxidation on platinum[J]. Nature, 1990, 343 (6256): 355- 357. DOI
2	KYOUNG J L , EDWARD C C , RAYMOND E , et al. Competing patterns of signaling activity in dictyostelium discoideum[J]. Physical Review Letters, 1996, 76 (7): 1173- 1177.
3	HUANG X Y , TROY W C , YANG Q , et al. Spiral waves in disinhibited mammalian neocortex[J]. The Journal of Neuroscience, 2004, 24 (44): 9897- 9902. DOI
4	DAVIDENKO J M , PERTSOV A V , SALOMONSZ R , et al. Stationary and drifting spiral waves of excitation in isolated cardiac muscle[J]. Nature, 1992, 355 (6358): 349- 351. DOI
5	BAI J , HUANG Z J , TANG G N . Terminating arrhythmia by using motion controller[J]. Chinese Journal of Computational Physics, 2021, 38 (3): 352- 360.
6	CHRISTOPH J , CHEBBOK M , RICHTER C , et al. Electromechanical vortex filaments during cardiac fibrillation[J]. Nature, 2018, 555 (7698): 667- 672. DOI
7	JAMES J W , QU Z L , CHEN P S , et al. The dynamics of cardiac fibrillation[J]. Circulation, 2005, 112 (8): 1232- 1240. DOI
8	HERVE H , RAPPEL W J . Dynamics of conduction blocks in a model of paced cardiac tissue[J]. Physical Review E, 2005, 71 (5): 051911. DOI
9	TAE Y K , HONG J H , RYOUN H , et al. Alternans by non-monotonic conduction velocity restitution, bistability and memory[J]. New Journal of Physics, 2013, 15 (1): 013046. DOI
10	ALAN K , JOSEPH S . Identification of conduction block in cardiac muscle: In vitro observations in canine epicardium[J]. Cardiovascular Research, 1994, 28 (2): 259- 269. DOI
11	YANN P , JAN P . Nonlinear behaviour of conduction and block in cardiac tissue with heterogeneous expression of connexin 43[J]. Journal of Molecular and Cellular Cardiology, 2014, 76, 46- 54. DOI
12	KEVIN J J , AJAY K M , RAMYA I . A case report of cardiac amyloidosis presenting with chronic pericardial effusion and conduction block[J]. European Heart Journal - Case Reports, 2019, 3 (4): 1- 7.
13	董力耘, 陈立, 段晓茵. 基于教室人群疏散实验的行人流建模和模拟[J]. 物理学报, 2015, 64 (22): 220505. DOI
14	NI X Y , HUANG H . A new cellular automaton model accounting for stochasticity in traffic flow induced by heterogeneity in driving behavior[J]. Chinese Physics B, 2019, 28 (9): 098901. DOI
15	YANG S Y , KIM J H . Cellular automaton calculation for dynamic recrystallization[J]. Journal of Physics Conference Series, 2018, 1063 (1): 012144.
16	LIU S W , WILLSHER J , BILITEWSKI T , et al. Butterfly effect and spatial structure of information spreading in a chaotic cellular automaton[J]. Physical Review B, 2021, 103 (9): 094109. DOI
17	ZHANG X L , TAN H L , TANG G N , et al. Mechanical deformation of myocardial tissue with cellular automaton[J]. Chinese Journal of Computational Physics, 2018, 35 (3): 294- 302.
18	MATSUBARA T , UEHARA K . Asynchronous network of cellular automaton-based neurons for efficient implementation of Boltzmann machines[J]. Nonlinear Theory and Its Applications, IEICE, 2018, 9 (1): 24- 35. DOI
19	GUAN F R , LI C Q , DENG M Y . Spiral wave dynamics of excited medium: Effect of relative refractory[J]. Chinese Journal of Computational Physics, 2021, 38 (6): 749- 756.
20	ITO H , GLASS L . Spiral breakup in a new model of discrete excitable media[J]. Physical Review Letters, 1991, 66 (5): 671- 674. DOI
21	张学良, 谭惠丽, 白克钊, 等. 一种体现心肌细胞传导记忆的元胞自动机模型[J]. 广西师范大学学报(自然科学版), 2017, 35 (4): 1- 9.
22	MERA S , TOON A B V V , RICHARD N W H , et al. A 50% reduction of excitability but not of intercellular coupling affects conduction velocity restitution and activation delay ion the mouse heart[J]. PloS One, 2011, 6 (6): e20310. DOI
23	欧阳颀. 反应扩散系统中螺旋波的失稳[J]. 物理, 2001, 30 (1): 30- 36.

[1]	Guowei WANG, Yan FU. Stochastic Boundary-induced Spatiotemporal Pattern Transformation in Izhikevich Neuronal Networks [J]. Chinese Journal of Computational Physics, 2023, 40(5): 622-632.
[2]	Furong GUAN, Chengqian LI, Minyi DENG. Spiral Wave Dynamics of Excited Medium: Effect of Relative Refractory [J]. Chinese Journal of Computational Physics, 2021, 38(6): 749-756.
[3]	ZHANG Xueliang, TAN Huili, TANG Guoning, DENG Minyi. Mechanical Deformation of Myocardial Tissue with Cellular Automaton [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(3): 294-302.
[4]	CHEN Xiqiong, DENG Minyi, TANG Guoning, KONG Lingjiang. Effect of Conduction Delay on Dynamics of Spiral Waves [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2013, 30(4): 620-626.
[5]	YAN Guang-wu. Lattice Boltzmann Model for Nonlinear Chemical Waves in the Excitable Media [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2003, 20(4): 356-358.