Multivariable Function Projective Synchronization of High Dimensional Chaotic Systems and Its Secure Communication Scheme

doi:10.19596/j.cnki.1001-246x.8550

Abstract

Abstract:

A modified function projective synchronization scheme, multivariable function projective synchronization, is proposed. Different from existing function projective synchronization schemes whose scaling factor is unary function, the scaling factor discussed in this scheme is multivariable function. It implies that synchronization behavior of the proposed scheme is more complicated and more unpredictable. The driver and responding system show correlation in a higher dimension. With modified active control method, controller of the synchronization is designed. In numerical simulations, four-dimensional energy resources system and a new hyperchaotic Chua system are investigated. Multivariable function projective synchronization with two types of scaling factor between two systems are achieved. Based on the synchronization, a secure communication scheme is designed. A secure communication simulation is carried out with sinusoidal signal and gray image signal as information signals. Meanwhile, anti-noise simulation is performed with a wavelet threshold denoising algorithm. It shows that the synchronization method is feasible, and the secure communication scheme is effective.

Key words: multivariable function projective synchronization, modified active control, secure communication, wavelet threshold denoising

Zhenbo LI, Yezhi TANG. Multivariable Function Projective Synchronization of High Dimensional Chaotic Systems and Its Secure Communication Scheme[J]. Chinese Journal of Computational Physics, 2023, 40(1): 91-105.

Figures/Tables 16

Table 1 Different kinds of projective synchronization

同步误差向量	同步类型	比例因子Γ
e_i=x_i-Γy_i 其中x_i为驱动向量，y_i为响应向量，Γ为比例因子	完全同步	Γ=1
	投影同步	Γ为常数，大小由驱动系统初值决定
	广义投影同步	Γ为常数，大小可任意指定
	一元函数投影同步	Γ为时间t的一元函数
	二元函数投影同步	Γ为二元函数
	多元函数投影同步	Γ为多元函数

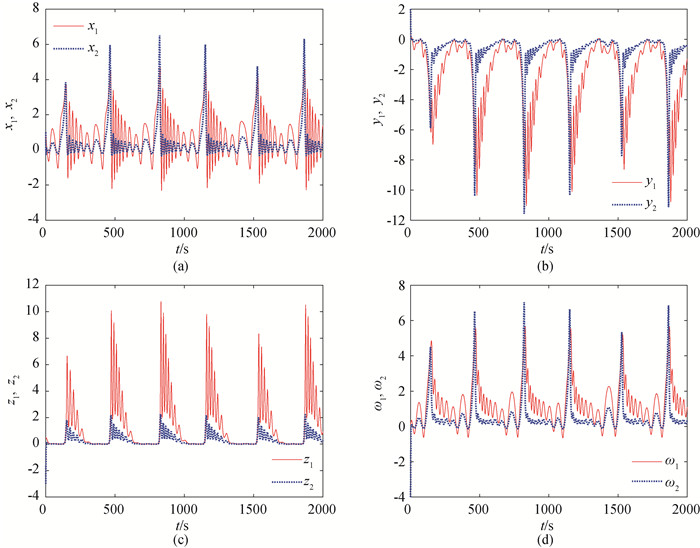
Fig.1 Time response of System (8) and (9) with scaling function Γ1 (a) time response of x1 and x2; (b) time response of y1 and y2; (c) time response of z1 and z2; (d) time response of ω1 and ω2

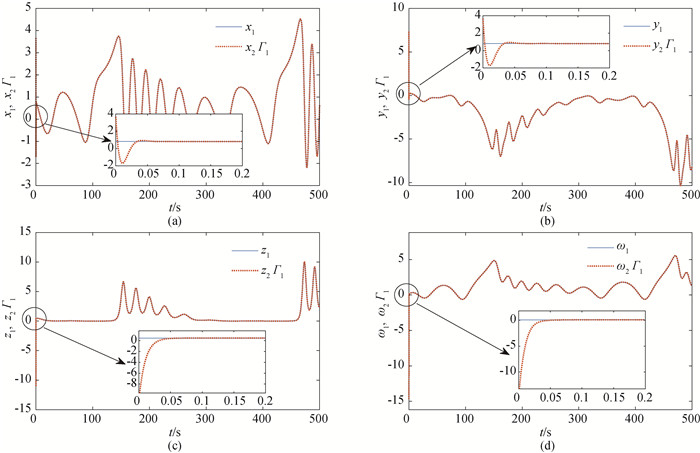
Fig.2 Phase portraits of System (8) and (9) with scaling function Γ1 (a) phase portraits in x-y-z space; (b) phase portraits in y-z-ω space

Fig.3 Synchronization results of System (8) and (9) with scaling function Γ1 (a) synchronization results of x1 and x2; (b) synchronization results of y1 and y2; (c) synchronization results of z1 and z2; (d) synchronization results of ω1 and ω2

Fig.4 Synchronization errors of System (8) and (9) with scaling function Γ1

Fig.5 Synchronization errors of System (8) and (9) with scaling function Γ1 at different ki (a) ki=1; (b) ki=10

Fig.6 Synchronization errors of System (8) and (9) (a) nonlinear feedback method, (b) adaptive feedback method

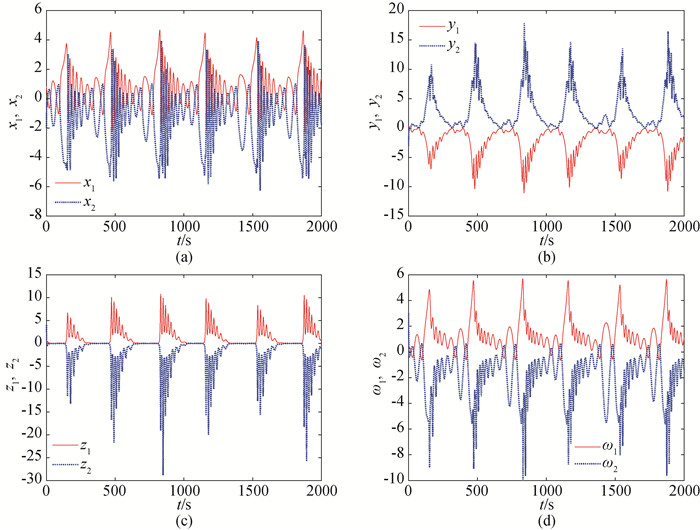
Fig.7 Time response of System (8) and (9) with scaling function Γ2 (a) time response of x1 and x2; (b) time response of y1 and y2; (c) time response of z1 and z2; (d) time response of ω1 and ω2

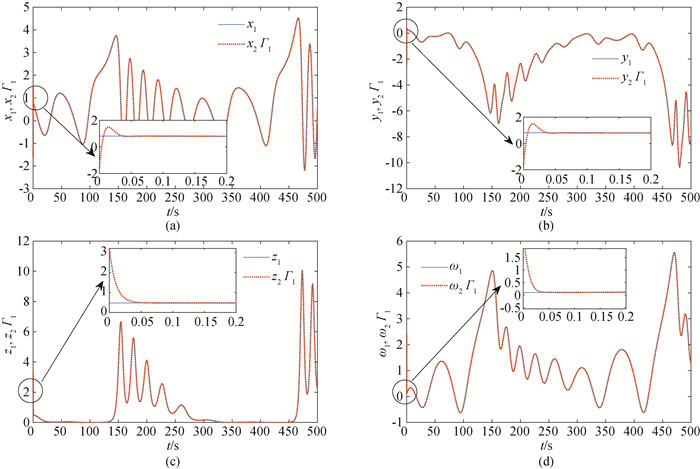
Fig.8 Phase portraits of System (8) and (9) with scaling function Γ2 (a) phase portrait in x-y-z space; (b) phase portrait in y-z-ω space

Fig.9 Synchronization results of System (8) and (9) with scaling function Γ2 (a) synchronization results of and x2; (b) synchronization results of y1 and y2; (c) synchronization results of z1 and z2; (d) synchronization results of ω1 and ω2

Fig.10 Synchronization errors of System (8) and (9) with scaling function Γ2

Fig.11 A flow chart of wavelet threshold denoising

Fig.12 A flow chart of secure communication scheme

Fig.13 Pictures of communication signal θ(t) at different SNR

Fig.14 Recovered signal of sinusoidal signal at different SNR

Fig.15 Recovered image of grayscale image at different SNR

References 33

1	PECORA L M , CARROLL T L . Synchronization in chaotic systems[J]. Physical Review Letters, 1990, 64 (8): 821- 824. DOI
2	SHI J P , LI P S , LIU G P . Synchronization control and parameter identification for unified chaotic system based on improved clonal selection algorithm[J]. Chinese Journal of Computational Physics, 2020, 37 (2): 240- 252.
3	YU H T , WANG J , LIU Q X , et al. Chaotic phase synchronization in a modular neuronal network of small-world subnetworks[J]. Chaos, 2011, 21 (4): 043125. DOI
4	FENG C F , YANG H J . Projective-lag synchronization scheme between two different discrete-time chaotic systems[J]. International Journal of Non-linear Mechanics, 2020, 121, 103451. DOI
5	MOSKALENKO O I , KORONOVSKII A A , SELSKII A O , et al. On multistability near the boundary of generalized synchronization in unidirectionally coupled chaotic systems[J]. Chaos, 2021, 31 (8): 083106. DOI
6	QIAN H , YU H J . Application of SC projective synchronization method in secure communication[J]. Chinese Journal of Computational Physics, 2016, 33 (1): 118- 126.
7	XUE W , ZHANG Y C . Application of conservative hyperchaos in digital image encryption[J]. Chinese Journal of Computational Physics, 2020, 37 (4): 498- 504.
8	KANG Z J , CANG S J , LI Y . A conservative-chaos-based key distribution protocol and image encryption algorithm[J]. Chinese Journal of Computational Physics, 2021, 38 (2): 232- 243.
9	MAINIERI R , REHACEK J . Projective synchronization in three-dimensional chaotic systems[J]. Physical Review Letters, 1999, 82 (15): 3042- 3045. DOI
10	CHEN Y , LI X . Function projective synchronization between two identical chaotic systems[J]. International Journal of Modern Physics C, 2007, 18 (5): 883- 888. DOI
11	DU H Y , ZENG Q S , WANG C H . Function projective synchronization of different chaotic systems with uncertain parameters[J]. Physics Letters A, 2008, 372 (33): 5402- 5410. DOI
12	SUDHEER K S , SABIR M . Adaptive modified function projective synchronization between hyperchaotic Lorenz system and hyperchaotic Lu system with uncertain parameters[J]. Physics Letters A, 2009, 373 (41): 3743- 3748. DOI
13	DU H Y , ZENG Q S , WANG C H . Modified function projective synchronization of chaotic system[J]. Chaos Solitons & Fractals, 2009, 42 (4): 2399- 2404.
14	YU Y G , LI H X . Adaptive generalized function projective synchronization of uncertain chaotic systems[J]. Nonlinear Analysis-Real World Applications, 2010, 11 (4): 2456- 2464. DOI
15	YUAN M M , WANG W P , LUO X , et al. Exponential lag function projective synchronization of memristor-based multidirectional associative memory neural networks via hybrid control[J]. Modern Physics Letters B, 2018, 32 (9): 1850116. DOI
16	CHAI X L , GAN Z H . Function Projective lag synchronization of chaotic systems with certain parameters via adaptive-impulsive control[J]. International Journal of Automation and Computing, 2019, 16 (2): 238- 247. DOI
17	WANG C , ZHANG H L , FAN W H , et al. Finite-time function projective synchronization control method for chaotic wind power systems[J]. Chaos Solitons & Fractals, 2020, 135, 109756.
18	EL-DESSOKY M M , ALZAHRANI E , AL-REHILY N . Control and adaptive modified function projective synchronization of a new hyperchaotic system[J]. Alexandria Engineering Journal, 2021, 60 (4): 3985- 3990. DOI
19	LI Z B , TANG J S . Generalized binary function projective synchronization of chaotic systems with unknown parameters[J]. Optik, 2017, 137, 101- 107. DOI
20	李震波, 赵小山, 王靖. 基于改进的主动控制法实现混沌系统广义投影同步[J]. 物理学报, 2011, 60 (5): 113- 120.
21	SUN M , JIA Q , TIAN L X . A new four-dimensional energy resources system and its linear feedback control[J]. Chaos Solitons & Fractals, 2009, 39 (1): 101- 108.
22	RECH P C , ALBUQUERQUE H A . A hyperchaotic Chua system[J]. International Journal of Bifurcation and Chaos, 2009, 19 (11): 3823- 3828. DOI
23	ROBINSON R C . An introduction to dynamical systems: Continuous and discrete[M]. New Jersey: Prentice Hall, 2004.
24	HU J B , HAN Y , ZHAO L D . Synchronizing chaotic systems using control based on a special matrix structure and extending to fractional chaotic systems[J]. Communications in Nonlinear Science and Numerical Simulation, 2010, 15 (1): 115- 123. DOI
25	LI W J , LI P , JIA M M . Chaos control and chaos synchronization of a multi-wing chaotic system and its application in multi-frequency weak signal detection[J]. Aip Advances, 2021, 11 (9): 095003. DOI
26	方洁, 娄新杰, 方娜, 等. 多混沌系统自适应组合函数投影同步[J]. 东北师大学报(自然科学版), 2020, 52 (1): 98- 103.
27	李爽, 徐伟, 李瑞红, 等. 异结构系统混沌同步的新方法[J]. 物理学报, 2006, (11): 5681- 5687.
28	REN L , ZHANG G S . Adaptive projective synchronization for a class of switched chaotic systems[J]. Mathematical Methods in The Applied Sciences, 2019, 42 (18): 6192- 6204. DOI
29	段青, 李凤祥, 田兆垒. 一种改进的小波阈值信号去噪方法[J]. 计算机仿真, 2009, 26 (4): 348- 351.
30	吴叶丽, 行鸿彦, 李瑾, 等. 改进阈值函数的小波去噪算法[J]. 电子测量与仪器学报, 2022, 36 (4): 9- 16.
31	付宏睿, 董永刚, 张建刚. 基于新四维混沌系统的复杂网络的混沌保密通信及噪声研究[J]. 东北师大学报(自然科学版), 2018, 50 (4): 73- 77.
32	王晓燕, 瞿少成, 田文汇, 等. 异结构混沌系统同步及其在保密通信中的应用[J]. 计算机应用研究, 2009, 26 (5): 1874- 1876.
33	于娜, 丁群, 陈红. 异结构系统混沌同步及其在保密通信中的应用[J]. 通信学报, 2007, (10): 73- 78.

[1]	Ya-qiong JIA, Bin YU. Differential Chaos Shift Keying Secure Communication System Based on Repeated Chaotic Spreading Sequence [J]. Chinese Journal of Computational Physics, 2022, 39(4): 491-497.
[2]	QIAN Hui, YU Hongjie. Application of SC Projective Synchronization Method in Secure Communication [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2016, 33(1): 117-126.