A Class of Preconditioners for Static Elastic Crack Problems Modeled by Extended Finite Element Method

doi:10.19596/j.cnki.1001-246x.8683

Abstract

Abstract:

This paper mainly discusses some effective domain decomposition preconditioners for static elastic crack problems modeled by geometrical extended finite element method. To construct the Schwarz type preconditioners, we adopt a special crack-tip domain decomposition strategy. The finite element mesh is decomposed into "crack tip" subdomains, which contain all the degrees of freedom (DOFs) of the branch enrichment functions, and "regular" subdomains, which contain the standard DOFs and the DOFs of the Heaviside enrichment functions. Based on the crack-tip domain decomposition strategy, an effective class of multiplicative and restrict multiplicative Schwarz preconditioners are derived. In the preconditioners, the crack tip subproblems are solved exactly and the regular subproblems are solved by some inexact solvers. Numerical experiments demonstrate the effectiveness of the preconditioners.

Key words: extended finite element method, domain decomposition, preconditioners, static crack problem

CLC Number:

O357.41

Hexiao FAN, Xingding CHEN. A Class of Preconditioners for Static Elastic Crack Problems Modeled by Extended Finite Element Method[J]. Chinese Journal of Computational Physics, 2024, 41(2): 151-160.

Figures/Tables 14

Fig.1 Linear elastic body with a crack (The domain Ω with boundary Γ and a crack Γc.)

Fig.2 Crack located on a structured mesh (Nodes in sets SH and SC are denoted by circles and squares, respectively.)

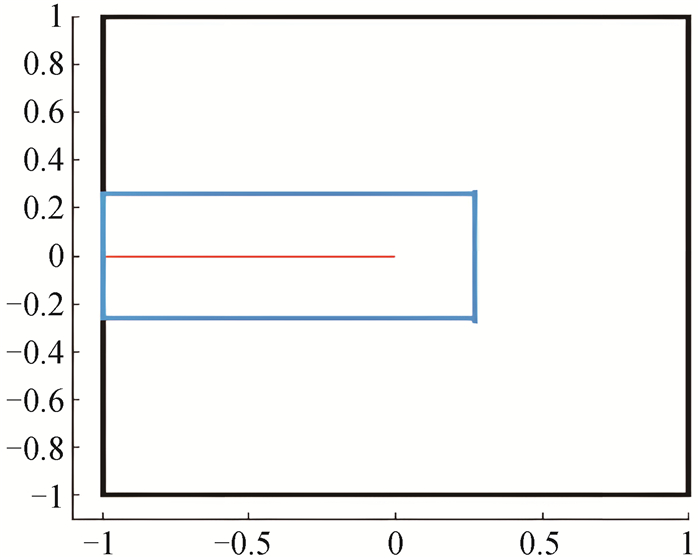
Fig.3 Schematic representation of two subdomains in the "crack line" domain decomposition (The red line denotes cracks, the blue subdomain denotes the "cracked" domain, the other is the "healthy" domain.)

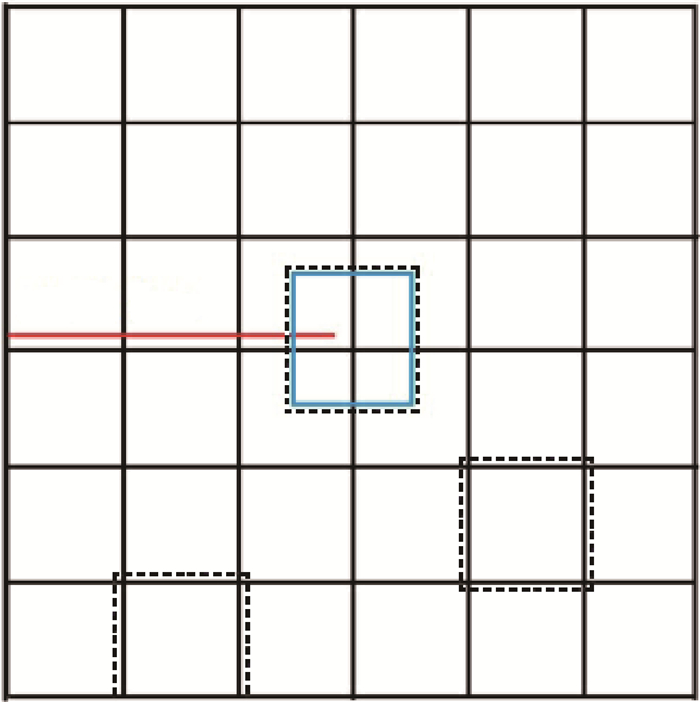
Fig.4 Schematic representation of subdomains in the "crack tip" domain decomposition(The blue subdomain denotes the "crack tip" domain, the black subdomains denote "regular" domains.)

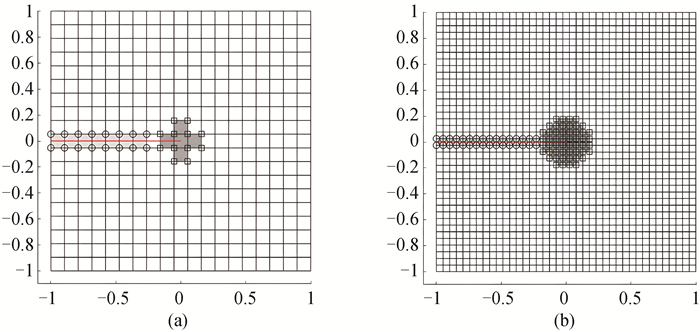
Fig.5 The initial geometry for the uniaxial tensile boundary crack problem

Fig.6 The geometric XFEM (The red line denotes the crack, nodes in sets SH and SG are denoted by circles and squares, respectively.) (a) the mesh scale is 19×19; (b) the mesh scale is 39×39

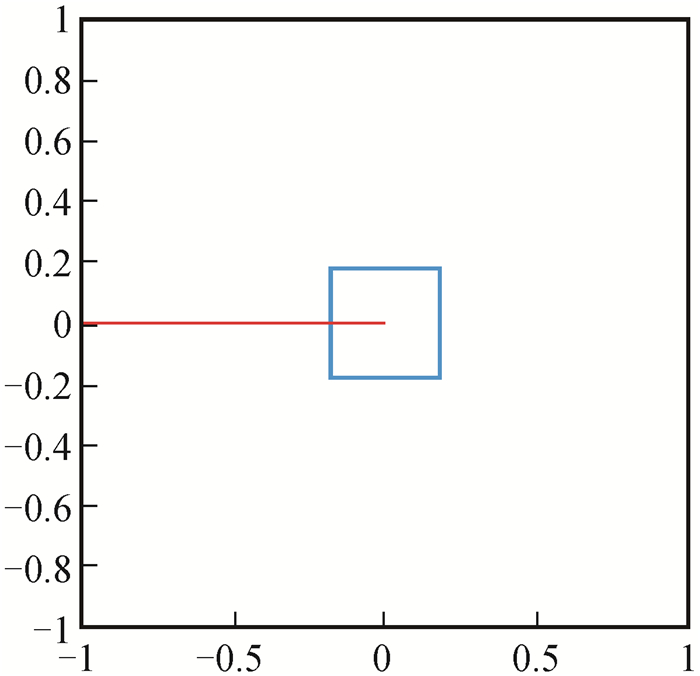
Fig.7 Schematic representation of two subdomains in the domain decomposition (The red line denotes cracks, the blue subdomain denotes the "crack tip" domain.)

Table 1 The condition number of the stiffness matrix for the two subdomains preconditioner (δ=2, CondNPre, CondRAS, CondRMS denotes condition number of the stiffness matrix with no preconditioner, with RAS preconditioner and with RMS preconditioner respectively.)

网格剖分	Cond_NPre	Cond_RAS	Cond_RMS
19×19	3.08×10⁶	7.40×10³	8.92×10³
39×39	1.62×10⁹	3.10×10⁶	3.76×10⁶
59×59	3.05×10¹⁰	4.22×10⁷	5.05×10⁷
79×79	2.13×10¹¹	2.19×10⁸	2.66×10⁸
99×99	1.43×10¹²	6.46×10⁸	1.20×10⁹
119×119	4.83×10¹²	3.10×10⁹	3.74×10⁹

Table 2 Number of iterations for two subdomains preconditioner (NonPre denotes no preconditioner, E denotes exact solution in the "regular" domain.)

网格剖分	NonPre	EAS	ERAS	EMS	ERMS
19×19	594	8	8	4	4
39×39	2 437	10	11	5	6
59×59	2 657	13	14	7	7
79×79	3 106	15	15	8	8
99×99	3 651	16	17	8	9
119×119	3 659	18	18	9	10

Table 3 Number of iterations for two subdomains preconditioner (Inexact solution by using ILU decomposition with a 10-3 drop tolerance in the "regular" domain.)

网格剖分	AS	RAS	MS	RMS
19×19	13	11	7	8
39×39	19	19	13	14
59×59	25	25	19	20
79×79	37	38	26	26
99×99	55	56	45	47
119×119	84	86	57	60

Table 4 Number of iterations for different preconditioners with a 4×4 patition, δ=1

网格剖分	NonPre	EAS	ERAS	EMS	ERMS
39×39	2 437	31	26	27	24
59×59	2 657	38	33	34	29
79×79	3 106	43	37	38	35
99×99	3 651	51	41	42	38
119×119	3 659	56	46	48	42
139×139	3 599	63	50	53	46
159×159	3 622	69	54	58	49

Table 5 Number of iterations for different preconditioners with a 4×4 patition, δ=2

网格剖分	EAS	ERAS	EMS	ERMS
39×39	28	22	24	20
59×59	30	26	26	24
79×79	35	29	30	27
99×99	39	33	34	30
119×119	42	36	37	34
139×139	47	39	39	35
159×159	52	41	43	38

Table 6 Number of iterations for different preconditioners with different patitions (δ=2, exact solutions in "regular" domains.)

网格剖分	4×4			6×6			8×8
网格剖分	ERAS	EMS	ERMS	ERAS	EMS	ERMS	ERAS	EMS	ERMS
39×39	22	24	20	26	29	23	30	29	29
59×59	26	26	24	32	35	28	37	41	34
79×79	29	30	27	36	41	35	41	47	37
99×99	33	34	30	41	50	38	47	57	42
119×119	36	37	34	44	48	41	53	63	48
139×139	39	39	35	48	55	45	58	71	54
159×159	41	43	38	55	59	51	63	72	58

Table 7 Number of iterations for different preconditioners with different patitions (δ=2, inexact solutions using ILU decomposition with a 10-3 drop tolerance in the "regular" domain.)

网格剖分	4×4			6×6			8×8
网格剖分	RAS	MS	RMS	RAS	MS	RMS	RAS	MS	RMS
39×39	24	26	22	27	29	24	32	29	26
59×59	34	36	30	40	39	34	41	42	38
79×79	47	47	43	49	48	45	50	52	46
99×99	57	59	54	56	62	54	58	64	55
119×119	77	75	72	74	73	69	75	75	70
139×139	85	84	82	86	83	81	86	87	82
159×159	109	109	106	115	117	110	104	107	101

References 22

1	高英俊, 罗志荣, 邓芊芊, 等. 韧性材料的微裂纹扩展与分叉的晶体相场模拟[J]. 计算物理, 2014, 31 (4): 471- 478.
2	黄朝琴, 姚军, 王月英, 等. 基于离散裂缝模型的裂缝性油藏注水开发数值模拟[J]. 计算物理, 2011, 28 (1): 41- 49.
3	李开泰, 黄艾香, 黄庆怀. 有限元方法及其应用[M]. 北京: 科学出版社, 2005: 1- 160.
4	BELYTSCHKO T , BLACK T . Elastic crack growth in finite elements with minimal remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 45 (5): 601- 620. DOI
5	庄茁, 柳占立, 成斌斌, 等. 扩展有限单元法[M]. 北京: 清华大学出版社, 2012: 35- 47.
6	杨璞, 牛红攀, 肖世富. 平面应变问题广义有限元法[J]. 计算物理, 2016, 33 (3): 358- 366.
7	BABUŠKA I , BANERJEE U . Stable generalized finite element method (SGFEM)[J]. Computer Methods in Applied Mechanics & Engineering, 2011, 201 (1): 91- 111.
8	GUPTA V , DUARTE C A , BABUŠKA I , et al. A stable and optimally convergent generalized FEM (SGFEM) for linear elastic fracture mechanics[J]. Computer Methods in Applied Mechanics & Engineering, 2013, 266 (1): 23- 39.
9	ZHANG Q H , BABUŠKA I , BANERJEE U . Robustness in stable generalized finite element methods (SGFEM) applied to Poisson problems with crack singularities[J]. Computer Methods in Applied Mechanics & Engineering, 2016, 311 (1): 476- 502.
10	田荣, 文龙飞. 改进型XFEM进展[J]. 计算力学学报, 2016, 33 (4): 469- 477.
11	ZHANG Q H . DOF-gathering stable generalized finite element methods for crack problems[J]. Numerical Methods for Partial Differential Equations, 2020, 36 (6): 1209- 1233. DOI
12	MENK A , BORDAS S P A . A robust preconditioning technique for the extended finite element method[J]. International Journal for Numerical Methods in Engineering, 2011, 85 (13): 1609- 1632. DOI
13	LANG C , MAKHIJA D , DOOSTAN A , et al. A simple and efficient preconditioning scheme for heaviside enriched XFEM[J]. Computational Mechanics: Solids, Fluids, Fracture Transport Phenomena and Variational Methods, 2014, 54 (5): 1357- 1374.
14	GILBERT S . Computational science and engineering[M]. Wellesley, MA: Wellesley-Cambridge Press, 2007: 551- 597.
15	WAISMAN H , BERGER-VERGIAT L . An adaptive domain decomposition preconditioner for crack propagation problems modeled by XFEM[J]. International Journal for Multiscale Computational Engineering, 2013, 11 (6): 633- 654. DOI
16	BERGER-VERGIAT L , WAISMAN H , HIRIYUR B , et al. Inexact Schwarz-algebraic multigrid preconditioners for crack problems modeled by extended finite element methods[J]. International Journal for Numerical Methods in Engineering, 2012, 90 (3): 311- 328. DOI
17	TIAN R, WEN L F. An extra dof-free and well-conditioned XFEM[C]//Proceedings of the 5th International Conference on Computational Methods, 2014: 784-793.
18	TIAN W , HUANG J J , JIANG Y , et al. A parallel scalable domain decomposition preconditioner for elastic crack simulation using XFEM[J]. International Journal for Numerical Methods in Engineering, 2022, 123 (15): 3393- 3417. DOI
19	GUPTA V , DUARTE C A , BABUŠKA I , et al. Stable GFEM (SGFEM): Improved conditioning and accuracy of GFEM/XFEM for three-dimensional fracture mechanics[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 289, 355- 386. DOI
20	GUPTA V , DUARTE C A , BABUŠKA I , et al. A stable and optimally convergent generalized FEM (SGFEM) for linear elastic fracture mechanics[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 266, 23- 39. DOI
21	SAAD Y . Iterative methods for sparse linear systems[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2000: 157- 218.
22	CAI X C , CHEN X D . Effective two-level domain decomposition preconditioners for elastic crack problems modeled by extended finite element method[J]. Communications in Computational Physics, 2020, 28 (4): 1561- 1584. DOI

[1]	YIN Liang, YANG Chao, MA Shizhuang. Parallel Numerical Simulations of Thermal Convection in the Earth's Outer Core Based on Domain Decomposition and Multigrid [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2019, 36(1): 1-14.
[2]	ZHANG Shouhui, LIANG Dong. A Strang-type Alternating Segment Domain Decomposition Method for Two-dimensional Parabolic Equations [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(4): 413-428.
[3]	TIAN Wei, REN Xincheng. Method of Moment for Electromagnetic Scattering from Ground Covered with Snow [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(2): 205-211.
[4]	LI Gang, ZHANG Baoyin, DENG Li, SHANGGUAN Danhua, LI Rui, MA Yan, FU Yuanguang, HU Xiaoli. Pseudo-Random Numbers for Identical Results on Varying Numbers of Processors in Domain Decomposed Particle Monte Carlo Simulations [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2017, 34(1): 67-72.
[5]	YE Zhenbao, ZHOU Haijing. High-order Discontinuous Galerkin Time-Domain Finite-Element Method for Three-dimensional Cavities [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2015, 32(4): 449-454.
[6]	CHEN Xue, SUN Chuang, XIA Xinlin. Stray Light Analysis Based on Domain Decomposition and Staged Ray Splitting [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2012, 29(6): 876-880.
[7]	WEI Junxia, YUAN Guangwei, YANG Shulin, SHEN Weidong. A Parallel Algorithm with Interface Prediction and Correction for Time-dependent Transport Equation in 2D Cylindrical Geometry [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2012, 29(2): 198-204.
[8]	SHENG Zhiming, CUI Xia, LIU Xingping. Domain Decomposition Algorithm witlI Multi-step Evaluation for Diffusion Equation [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2011, 28(6): 825-830.
[9]	BAI Xiaoyong, HE Yingbo, CHEN Chengjun. A Parallel Contact Detection Algorithm for Explicit Finite Element Analysis [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2011, 28(3): 341-346.
[10]	SHANG Yueqiang, HE Yinnian. Parallel Finite Element Algorithms Based on Fully Overlapping Domain Decomposition for Time-dependent Navier-Stokes Equations [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2011, 28(2): 181-187.
[11]	XIAN Yongli, DU Hongwei, WANG Congzheng, PENG Hu. A Fast Algorithm for Nonlinear Finite Sound Beams Based on Spatial-domain Decomposition [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2011, 28(1): 57-65.
[12]	WEI Junxia, YANG Shulin, FU Lianxiang. Parallel Domain Decomposition for Neutron Transport Equations with 2-D Cylindrical Geometry [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2010, 27(1): 1-7.
[13]	LIU Peng. Direct Domain Decomposition Method for Bistatic Scattering from 3-D Rough Surfaces [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2010, 27(1): 73-81.
[14]	FAN Xuanhua, WU Ruian, HAO Zhiming, HE Yingbo. Parallel Computing of Clamp Structure in Tahoe Frame [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2009, 26(5): 699-702.
[15]	YUAN Yirang. Recent Progress in Numerical Methods for Semiconductor Devices [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2009, 26(3): 317-324.