Chinese Journal of Computational Physics ›› 2024, Vol. 41 ›› Issue (5): 663-669.DOI: 10.19596/j.cnki.1001-246x.8798
• Research Reports • Previous Articles Next Articles
Batur AYGUL( ), Jinfeng ZHANG, Hamutjan AKBAR, Abliz AHMAD(
), Jinfeng ZHANG, Hamutjan AKBAR, Abliz AHMAD( )
)
Received:2023-07-06
Online:2024-09-25
Published:2024-09-14
Contact:
Abliz AHMAD
CLC Number:
Batur AYGUL, Jinfeng ZHANG, Hamutjan AKBAR, Abliz AHMAD. Effects of X Direction KSEA Interaction on Geometric Quantum Discord[J]. Chinese Journal of Computational Physics, 2024, 41(5): 663-669.
Add to citation manager EndNote|Ris|BibTeX
URL: http://www.cjcp.org.cn/EN/10.19596/j.cnki.1001-246x.8798
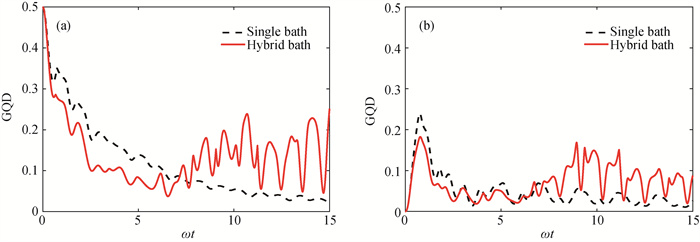
Fig.1 Dynamical evolution of geometric quantum discord in a non-Markov hybrid bath and non-Markov single bath with X-direction KSEA interaction (a) the initial states $|\psi\rangle=(|00\rangle-|11\rangle) / \sqrt{2}$ and (b) |φ〉= 10〉, kA=kB=1, Jx=0.2, Jy=0.4, Jz=0.9, γ=0.7, Dx=0.4, Γx=0.8
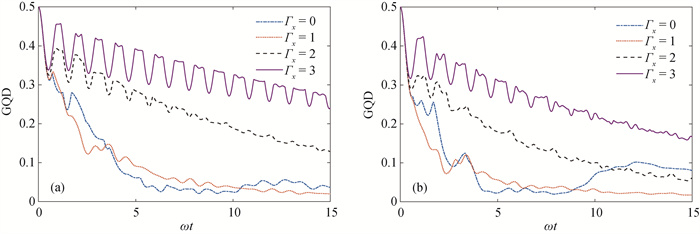
Fig.2 Effects of KSEA interactions on dynamics of geometric quantum discord in (a) hybird non-Markov and (b) single non-Markov environments,the initial state $|\psi\rangle=(|00\rangle-|11\rangle) / \sqrt{2}$,kA=kB=1,Jx=0.2,Jy=0.4,Jz=0.9,γ=0.7,Dx=0.4
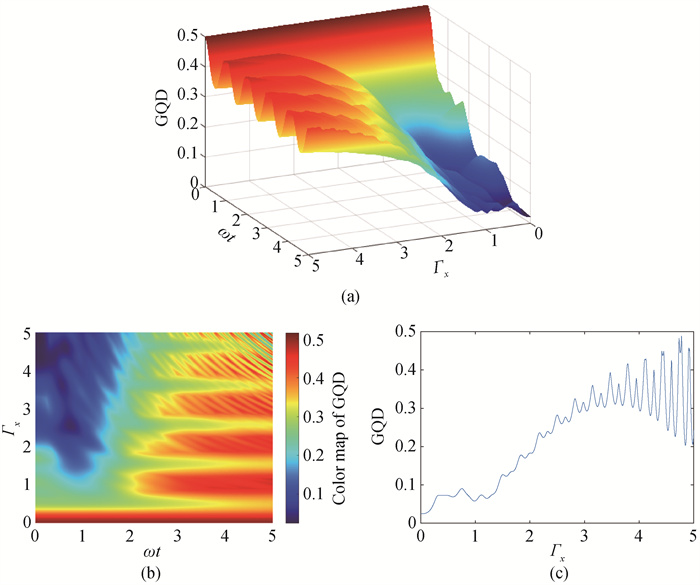
Fig.3 (a) 3-D projection diagram and (b) 3-D diagram of geometric quantum discord with time and KSEA interaction in hybird non-Markov environment, the initial state $|\psi\rangle=(|00\rangle-|11\rangle) / \sqrt{2}$; (c) effect of KSEA interactions on geometric quantum discord in hybird non-Markov environments at ωt=5, the initial state |φ〉= 10〉, Jx=0.2, Jy=0.4, Jz=0.9, γ=0.7, Dx=0.4
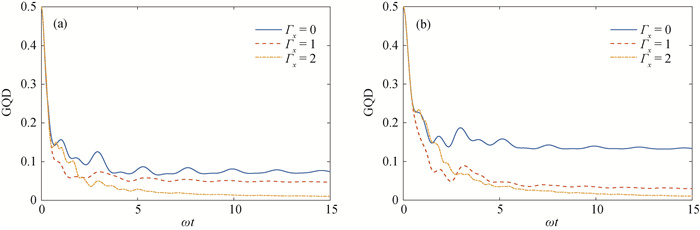
Fig.4 Dynamics of geometric quantum discord under (a) Markov hybrid bath and (b) Markov single bath with KSEA interaction, the initial state $|\psi\rangle=(|00\rangle-|11\rangle) / \sqrt{2}$, kA=kB=1, Jx=0.2, Jy=0.4, Jz=0.9, γ=3, Dx=0.4
| 1 |
BENNETT C H , DIVINCENZO D P . Quantum information and computation[J]. Nature, 2000, 404 (6775): 247- 255.
DOI |
| 2 |
BENNETT C H , BRASSARD G , CRÉPEAU C , et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels[J]. Physical Review Letters, 1993, 70 (13): 1895- 1899.
DOI |
| 3 |
HORODECKI R , HORODECKI P , HORODECKI M , et al. Quantum entanglement[J]. Reviews of Modern Physics, 2009, 81 (2): 865- 942.
DOI |
| 4 | OLLIVIER H , ZUREK W H . Quantum discord: A measure of the quantumness of correlations[J]. Physical Review Letters, 2002, 88 (1): 017901. |
| 5 |
DACIK B , VEDRAL V , BRUKNER C . Necessary and sufficient condition for nonzero quantum discord[J]. Physical Review Letters, 2010, 105 (19): 190502.
DOI |
| 6 |
DACIK B , LIPP Y O , MA Xiaosong , et al. Quantum discord as resource for remote state preparation[J]. Nature Physics, 2012, 8 (9): 666- 670.
DOI |
| 7 |
HU Mingliang , HU Xueyuan , WANG Jieci , et al. Quantum coherence and geometric quantum discord[J]. Physics Reports, 2018, 762/764, 1- 100.
DOI |
| 8 | DAOUD M , KAYDI W , EI HADFI H . Distribution of geometric quantum discord in photon-added coherent states[J]. Modern Physics Letters B, 2015, 29 (35/36): 1550239. |
| 9 |
SERI A , LENHARD A , RIELÄNDER D , et al. Quantum correlations between single telecom photons and a multimode on-demand solid-state quantum memory[J]. Physical Review X, 2017, 7 (2): 021028.
DOI |
| 10 |
BURKARD G , LOSS D , DIVINCENZO D P . Coupled quantum dots as quantum gates[J]. Physical Review B, 1999, 59 (3): 2070- 2078.
DOI |
| 11 | 黄睿, 吴绍全, 闫从华. 旁耦合于介观环与铁磁电极量子点系统中的自旋极化输运[J]. 计算物理, 2011, 28 (1): 131- 137. |
| 12 |
郑文礼, 李志文, 孙艳秀, 等. 双电子平面量子点基态能量的计算[J]. 计算物理, 2008, 25 (5): 617- 622.
DOI |
| 13 |
VRIJEN R , YABLONOVITCH E , WANG Kang , et al. Electron-spin-resonance transistors for quantum computing in silicon-germanium heterostructures[J]. Physical Review A, 2000, 62 (1): 012306.
DOI |
| 14 |
KANE B E . A silicon-based nuclear spin quantum computer[J]. Nature, 1998, 393 (6681): 133- 137.
DOI |
| 15 |
MORIYA T . New Mechanism of anisotropic superexchange interaction[J]. Physical Review Letters, 1960, 4 (5): 228- 230.
DOI |
| 16 |
KAPLAN T A . Single-band Hubbard model with spin-orbit coupling[J]. Zeitschrift für Physik B Condensed Matter, 1983, 49 (4): 313- 317.
DOI |
| 17 |
SHEKHTMAN L , AHARONY A , ENTIN-WOHLMAN O . Bond-dependent symmetric and antisymmetric superexchange interactions in La2CuO4[J]. Physical Review B, Condensed Matter, 1993, 47 (1): 174- 182.
DOI |
| 18 |
TSUKADA I , TAKEYA J , MASUDA T , et al. Weak ferromagnetism of quasi-one-dimensional S=1/2 antiferromagnet BaCu2Ge2O7[J]. Physical Review B, 2000, 62 (10): R6061- R6064.
DOI |
| 19 |
ZHELUDEV A , MASLOV S , SHIRANE G , et al. Magnetic anisotropy and low-energy spin waves in the Dzyaloshinskii-Moriya spiral magnet Ba2CuGe2O7[J]. Physical Review B, 1999, 59 (17): 11432- 11444.
DOI |
| 20 |
ZHELUDEV A , MASLOV S , TSUKADA I , et al. Experimental evidence for kaplan-shekhtman-entin-wohlman-aharony interactions in Ba2CuGe2O7[J]. Physical Review Letters, 1998, 81 (24): 5410- 5413.
DOI |
| 21 |
ELGHAAYDA S , KHEDR A N , TAMMAM M , et al. Quantum entanglement versus skew information correlations in dipole-dipole system under KSEA and DM interactions[J]. Quantum Information Processing, 2023, 22 (2): 117.
DOI |
| 22 |
KHEDIF Y , ERREHYMY A , DAOUD M . Behavior of local quantum fisher information and local quantum uncertainty in dipolar spin system with DM and KSEA interactions[J]. Modern Physics Letters A, 2022, 37 (22): 2250147.
DOI |
| 23 |
FEDOROVA A V , YURISCHEV M A . Quantum entanglement in the anisotropic Heisenberg model with multicomponent DM and KSEA interactions[J]. Quantum Information Processing, 2021, 20 (5): 169.
DOI |
| 24 |
OUMENNANA M , DAHBI Z , MANSOUR M , et al. Geometric measures of quantum correlations in a two-qubit heisenberg XXZ model under multiple interactions effects[J]. Journal of Russian Laser Research, 2022, 43, 533- 545.
DOI |
| 25 | BREUER H P , PETRUCCIONE F . The theory of open quantum systems[M]. New York: Oxford University Press, 2007: 219- 280. |
| 26 |
DIÓSI L , STRUNZ W T . The non-Markovian stochastic schrödinger equation for open systems[J]. Physics Letters A, 1997, 235 (6): 569- 573.
DOI |
| 27 |
DIÓSI L , GISIN N , STRUNZ W T . Non-Markovian quantum state diffusion[J]. Physical Review A, 1998, 58 (3): 1699- 1712.
DOI |
| 28 |
JING J , ZHAO X , YOU J , et al. Many-body quantum trajectories of non-Markovian open systems[J]. Physical Review A, 2013, 88 (5): 052122.
DOI |
| 29 |
CHEN Yusui , YOU J Q , YU Ting . Exact non-Markovian master equations for multiple qubit systems: Quantum-trajectory approach[J]. Physical Review A, 2014, 90 (5): 052104.
DOI |
| 30 |
ZHAO Xinyu , JING Jun , CORN B , et al. Dynamics of interacting qubits coupled to a common bath: Non-Markovian quantum-state-diffusion approach[J]. Physical Review A, 2011, 84 (3): 032101.
DOI |
| 31 |
ZHAO Xinyu , SHI Wufu , WU Lianao , et al. Fermionic stochastic Schrödinger equation and master equation: An open-system model[J]. Physical Review A, 2012, 86 (3): 032116.
DOI |
| 32 | 唐诗生, 艾合买提·阿不力孜. 非马尔科夫环境中各向异性海森堡自旋链的量子失协[J]. 计算物理, 2022, 39 (2): 165- 172. |
| 33 |
LACROIX D , SARGSYAN V V , ADAMIAN G G , et al. Non-Markovian modeling of Fermi-Bose systems coupled to one or several Fermi-Bose thermal baths[J]. Physical Review A, 2020, 102 (2): 022209.
DOI |
| 34 |
RITSCHEL G , SUESS D , MÖBIUS S , et al. Non-Markovian quantum state diffusion for temperature-dependent linear spectra of light harvesting aggregates[J]. The Journal of Chemical Physics, 2015, 142 (3): 034115.
DOI |
| 35 |
LAMBERT N , NORI F . Detecting quantum-coherent nanomechanical oscillations using the current-noise spectrum of a double quantum dot[J]. Physical Review B, 2008, 78 (21): 214302.
DOI |
| 36 |
AHMADI F , HASELI S , HADIPOUR M , et al. Quantum speed limit time of topological qubits influenced by the fermionic and bosonic environments[J]. Brazilian Journal of Physics, 2022, 52 (3): 85.
DOI |
| 37 |
BÄTGE J , KE Y , KASPAR C , et al. Nonequilibrium open quantum systems with multiple bosonic and fermionic environments: A hierarchical equations of motion approach[J]. Physical Review B, 2021, 103 (23): 235413.
DOI |
| 38 |
ZHAO Xinyu , SHI Wufu , YOU Jq , et al. Non-Markovian dynamics of quantum open systems embedded in a hybrid environment[J]. Annals of Physics, 2017, 381, 121- 136.
DOI |
| 39 | 艾克拜尔·阿木提江, 阿拉帕提·阿不力米提, 杨帆, 等. 混杂非马尔可夫库对海森伯XYZ自旋链模型的量子纠缠与量子稠密编码的影响[J]. 激光与光电子学进展, 2022, 59 (5): 320- 326. |
| 40 | 杨帆, 阿拉帕提·阿不力米提, 艾合买提·阿不力孜. 非马尔可夫环境下Dzyaloshinskii-Moriya相互作用和非均匀磁场对自旋系统的纠缠影响[J]. 激光与光电子学进展, 2021, 58 (7): 372- 379. |
| 41 | 张金峰, 阿拉帕提·阿不力米提, 杨帆, 等. 不同外加磁场中Kaplan-Shekhtman-Entin-Wohlman-Aharony相互作用对量子失协非马尔科夫演化的影响[J]. 物理学报, 2021, 70 (22): 40- 47. |
| [1] | Shisheng TANG, AHMAT Abliz. Quantum Discord of Heisenberg XYZ Spin Chain in Non-Markovian Environment [J]. Chinese Journal of Computational Physics, 2022, 39(2): 165-172. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||
Copyright © Chinese Journal of Computational Physics
E-mail: jswl@iapcm.ac.cn
Supported by Beijing Magtech Co., Ltd.
