Chinese Journal of Computational Physics ›› 2022, Vol. 39 ›› Issue (2): 223-232.DOI: 10.19596/j.cnki.1001-246x.8364
• Research Reports • Previous Articles Next Articles
Jian PAN( ), Zhaoli GUO*(
), Zhaoli GUO*( ), Songze CHEN*(
), Songze CHEN*( )
)
Received:2021-03-24
Online:2022-03-25
Published:2022-06-24
Contact:
Zhaoli GUO, Songze CHEN
Jian PAN, Zhaoli GUO, Songze CHEN. A Compound Neural Network for Learning Partial Differential Equations from Noisy Data[J]. Chinese Journal of Computational Physics, 2022, 39(2): 223-232.
Add to citation manager EndNote|Ris|BibTeX
URL: http://www.cjcp.org.cn/EN/10.19596/j.cnki.1001-246x.8364
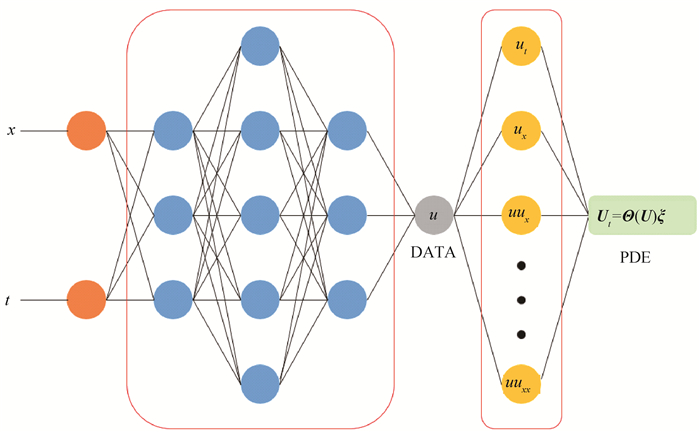
Fig.2 Structure of a compound neural network (The blue part represents the network that approximates solution of the equation. The yellow part represents the constructed candidate library. The DATA part represents residual of the data. The PDE part represents residual of the constructed governing equation.)
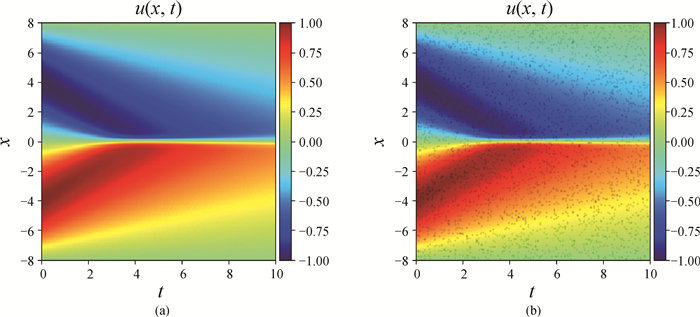
Fig.3 (a) Solution of Burgers equation in the form of heat map and (b) a portion of the map indicating 3000 data selected randomly from the dataset (The background represents the solution u in the dataset by heat map, and the black dots are selected data.)
| 噪声数据量 | NN-PDE | STRidge |
| 无 | ut=- 0.9988 uux+0.0999 uxx | ut=- 1.001 uux+0.102 uxx |
| 1% | ut=- 0.9965 uux+0.0997 uxx | ut=- 0.960 uux+0.102 uxx |
| 5% | ut=- 0.9992 uux+0.1003 uxx | ut=- 0.824 uux+0.117 uxx - 0.06 u2uxx |
| 10% | ut=- 0.9789 uux+0.0998 uxx | 无法得到简约的方程 |
Table 1 Performance of NN-PDE and STRidge in different noises for Burgers equation ut=- uux+0.1uxx
| 噪声数据量 | NN-PDE | STRidge |
| 无 | ut=- 0.9988 uux+0.0999 uxx | ut=- 1.001 uux+0.102 uxx |
| 1% | ut=- 0.9965 uux+0.0997 uxx | ut=- 0.960 uux+0.102 uxx |
| 5% | ut=- 0.9992 uux+0.1003 uxx | ut=- 0.824 uux+0.117 uxx - 0.06 u2uxx |
| 10% | ut=- 0.9789 uux+0.0998 uxx | 无法得到简约的方程 |
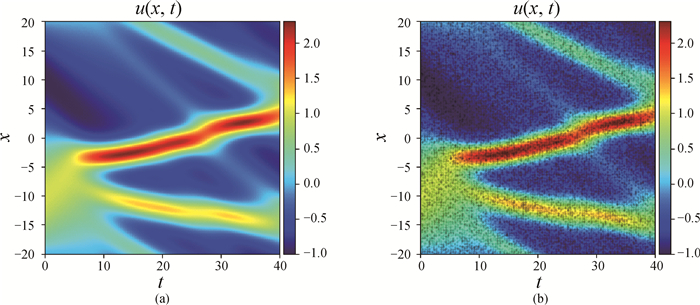
Fig.4 (a) Solution of KdV equation in the form of heat map and (b) a portion of the map indicating 25 000 data selected randomly from the dataset (The background represents solution u in the dataset by heat map, and the black dots are selected data.)
| 噪声数据量 | NN-PDE | DL-PDE |
| 无 | ut=- 0.9995 uux - 0.9995 uxxx | ut=- 0.993 uux - 0.996 uxxx |
| 1% | ut=- 0.9986 uux - 0.9991 uxxx | ut=- 0.986 uux - 0.985 uxxx |
| 5% | ut=- 0.9995 uux - 0.9973 uxxx | ut=- 0.968 uux - 0.974 uxxx |
| 10% | ut=- 1.0018 uux - 1.0023 uxxx | ut=- 0.940 uux - 0.936 uxxx |
Table 2 Performance of NN-PDE and STRidge in different noises for KdV equation ut=- uux - uxxx
| 噪声数据量 | NN-PDE | DL-PDE |
| 无 | ut=- 0.9995 uux - 0.9995 uxxx | ut=- 0.993 uux - 0.996 uxxx |
| 1% | ut=- 0.9986 uux - 0.9991 uxxx | ut=- 0.986 uux - 0.985 uxxx |
| 5% | ut=- 0.9995 uux - 0.9973 uxxx | ut=- 0.968 uux - 0.974 uxxx |
| 10% | ut=- 1.0018 uux - 1.0023 uxxx | ut=- 0.940 uux - 0.936 uxxx |
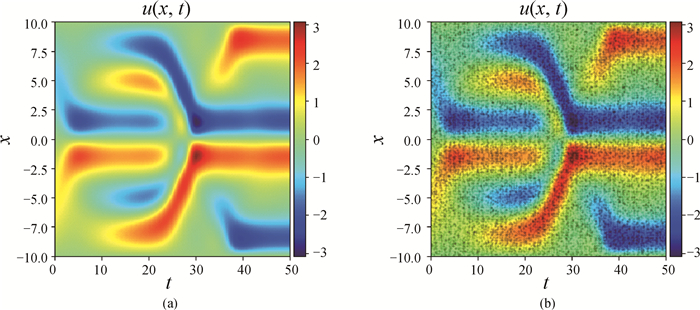
Fig.5 (a) Solution of KS equation in the form of heat map and (b) a portion of the map indicating 25 000 data selected randomly from the dataset (The background represents the solution u in the dataset by heat map, and the black dots are selected data.)
| 噪声数据量 | 控制方程 |
| 无 | ut=- 0.9969 uux - 0.9966 uxx - 0.9972 uxxxx |
| 1% | ut=- 0.9982 uux - 0.9954 uxx - 0.9964 uxxxx |
| 5% | ut=- 0.9962 uux - 0.9946 uxx - 0.9955 uxxxx |
| 10% | ut=- 0.9780 uux - 1.0020 uxx - 0.9964 uxxxx |
Table 3 Performance of NN-PDE and STRidge in different noises for KS equation ut=- uux - uxx - uxxxx
| 噪声数据量 | 控制方程 |
| 无 | ut=- 0.9969 uux - 0.9966 uxx - 0.9972 uxxxx |
| 1% | ut=- 0.9982 uux - 0.9954 uxx - 0.9964 uxxxx |
| 5% | ut=- 0.9962 uux - 0.9946 uxx - 0.9955 uxxxx |
| 10% | ut=- 0.9780 uux - 1.0020 uxx - 0.9964 uxxxx |
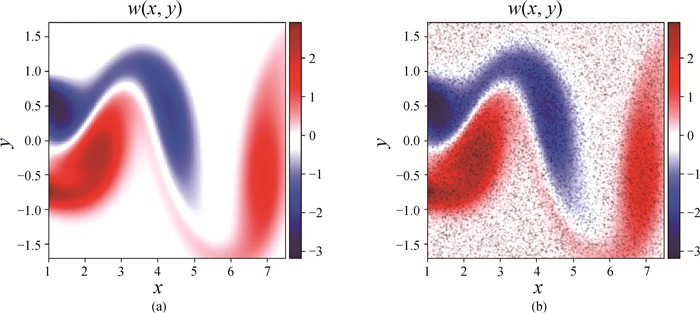
Fig.6 (a) Solution of NS equation in the form of heat map and (b) a portion of the map indicating 50 000 data selected randomly from the dataset (The background represents the solution w in the dataset by heat map, and the black dots are selected data.)
| 噪声数据量 | 控制方程 |
| 无 | wt=- 0.9995 uwx- 0.9986 vwy+0.0100 wxx+0.0100 wyy |
| 1% | wt=- 0.9993 uwx- 0.9982 vwy+0.0100 wxx+0.0100 wyy |
| 5% | wt=- 0.9988 uwx- 0.9919 vwy+0.0100 wxx+0.0100 wyy |
| 10% | wt=- 0.9936 uwx- 0.9729 vwy+0.0095 wxx+0.0108 wyy |
Table 4 Performance of NN-PDE and STRidge in different noises for NS equation wt=- uwx - vwy+0.01(wxx+wyy)
| 噪声数据量 | 控制方程 |
| 无 | wt=- 0.9995 uwx- 0.9986 vwy+0.0100 wxx+0.0100 wyy |
| 1% | wt=- 0.9993 uwx- 0.9982 vwy+0.0100 wxx+0.0100 wyy |
| 5% | wt=- 0.9988 uwx- 0.9919 vwy+0.0100 wxx+0.0100 wyy |
| 10% | wt=- 0.9936 uwx- 0.9729 vwy+0.0095 wxx+0.0108 wyy |
| 1 |
DOI |
| 2 |
DOI |
| 3 |
DOI |
| 4 |
DOI |
| 5 |
DOI |
| 6 |
DOI |
| 7 |
DOI |
| 8 |
DOI |
| 9 |
DOI |
| 10 |
DOI |
| 11 |
DOI |
| 12 |
|
| 13 |
DOI |
| 14 |
KNOWLES I, RENKA R J. Methods for numerical differentiation of noisy data[J]. Electronic Journal of Differential Equations, Conference 21(2014): 235-246.
|
| 15 |
DOI |
| 16 |
DOI |
| 17 |
DOI |
| 18 |
DOI |
| 19 |
|
| 20 |
|
| 21 |
DOI |
| 22 |
|
| 23 |
|
| [1] | MEI Shu-li, LU Qi-shao, ZHANG Sen-wen. An Adaptive Wavelet Precise Integration Method for Partial Differential Equations [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2004, 21(6): 523-530. |
| [2] | Zhang Zhengke, Zhuang Fenggan, Zhu Ziqiang, Luo Shijun. RESEARCH OF GRID SPACING AND ORTHOGONALITY CONTROL IN THREE DIMENSIONAL FLOWS AROUND A WING BODY TAIL COMBINATION [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 1997, 14(2): 247-252. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||
Copyright © Chinese Journal of Computational Physics
E-mail: jswl@iapcm.ac.cn
Supported by Beijing Magtech Co., Ltd.
