Chinese Journal of Computational Physics ›› 2022, Vol. 39 ›› Issue (4): 427-439.DOI: 10.19596/j.cnki.1001-246x.8447
Previous Articles Next Articles
Qiao-ling ZHANG1, He-fang JING1,2,*( )
)
Received:2021-09-13
Online:2022-07-25
Published:2022-11-17
Contact:
He-fang JING
Qiao-ling ZHANG, He-fang JING. Flow Patterns in Three-dimensional Lid-driven Cavities with Curved Boundary: MRT-LBM Study[J]. Chinese Journal of Computational Physics, 2022, 39(4): 427-439.
Add to citation manager EndNote|Ris|BibTeX
URL: http://www.cjcp.org.cn/EN/10.19596/j.cnki.1001-246x.8447
| 模型 | cs/c | ci/c | ωi |
| D3Q15 | (0, 0, 0) | 2/9 (i = 0) | |
| (±1, 0, 0), (0, ±1, 0), (0, 0, ±1) | 1/9 (i = 1~6) | ||
| (±1, ±1, ±1) | 1/72 (i = 7~14) | ||
| D3Q19 | (0, 0, 0) | 1/3 (i = 0) | |
| (±1, 0, 0), (0, ±1, 0), (0, 0, ±1) | 1/18 (i = 1~6) | ||
| (±1, ±1, 0), (±1, 0, ±1), (0, ±1, ±1) | 1/36 (i = 7~18) | ||
| D3Q27 | (0, 0, 0) | 8/27 (i = 0) | |
| (±1, 0, 0), (0, ±1, 0), (0, 0, ±1) | 2/27 (i = 1~6) | ||
| (±1, ±1, 0), (±1, 0, ±1), (0, ±1, ±1) | 1/54 (i = 7~18) | ||
| (±1, ±1, ±1) | 1/216 (i = 19~26) |
Table 1 Essential parameters in D3Q15, D3Q19 and D3Q27 models
| 模型 | cs/c | ci/c | ωi |
| D3Q15 | (0, 0, 0) | 2/9 (i = 0) | |
| (±1, 0, 0), (0, ±1, 0), (0, 0, ±1) | 1/9 (i = 1~6) | ||
| (±1, ±1, ±1) | 1/72 (i = 7~14) | ||
| D3Q19 | (0, 0, 0) | 1/3 (i = 0) | |
| (±1, 0, 0), (0, ±1, 0), (0, 0, ±1) | 1/18 (i = 1~6) | ||
| (±1, ±1, 0), (±1, 0, ±1), (0, ±1, ±1) | 1/36 (i = 7~18) | ||
| D3Q27 | (0, 0, 0) | 8/27 (i = 0) | |
| (±1, 0, 0), (0, ±1, 0), (0, 0, ±1) | 2/27 (i = 1~6) | ||
| (±1, ±1, 0), (±1, 0, ±1), (0, ±1, ±1) | 1/54 (i = 7~18) | ||
| (±1, ±1, ±1) | 1/216 (i = 19~26) |
| 腔体类型 | Xmax | Ymax | Zmax | SL | 腔体特殊参数 |
| 长方体腔 | 56 | 56 | 28 | 2.02 | |
| 圆柱腔 | 28 | 2.02 | 底面直径=56;高度=28 | ||
| 半圆柱腔 | 28 | 1.57 | 底面直径=56;高度=56 | ||
| 旋转双曲面腔 | 20 | 1.18 | 实半轴=2;虚半轴=3 | ||
| 旋转椭球面腔 | 20 | 2.81 | 长半轴=28;短半轴=20 | ||
| 半球腔 | 28 | 1.57 | 直径=56 | ||
| “上圆柱+下半球”腔 | 56 | 2.57 | 圆柱高=28;半球高=28 | ||
| “上长方体+下半圆柱”腔 | 56 | 2.57 | 长方体高=28;半圆柱高=28 |
Table 2 Typical parameters of various cavities
| 腔体类型 | Xmax | Ymax | Zmax | SL | 腔体特殊参数 |
| 长方体腔 | 56 | 56 | 28 | 2.02 | |
| 圆柱腔 | 28 | 2.02 | 底面直径=56;高度=28 | ||
| 半圆柱腔 | 28 | 1.57 | 底面直径=56;高度=56 | ||
| 旋转双曲面腔 | 20 | 1.18 | 实半轴=2;虚半轴=3 | ||
| 旋转椭球面腔 | 20 | 2.81 | 长半轴=28;短半轴=20 | ||
| 半球腔 | 28 | 1.57 | 直径=56 | ||
| “上圆柱+下半球”腔 | 56 | 2.57 | 圆柱高=28;半球高=28 | ||
| “上长方体+下半圆柱”腔 | 56 | 2.57 | 长方体高=28;半圆柱高=28 |
| 腔体形状 | y/Ymax= 0.15 | y/Ymax= 0.3 | y/Ymax= 0.38 | y/Ymax= 0.5 |
| 长方体腔 | (0.77, 0.15, 0.55) | (0.68, 0.30, 0.58) | (0.59, 0.38, 0.58) | (0.54, 0.50, 0.58) |
| 圆柱腔 | (0.70, 0.15, 0.62) | (0.65, 0.30, 0.45) | (0.33, 0.38, 0.41) | (0.25, 0.50, 0.38) |
| 半圆柱腔 | (0.70, 0.15, 0.52) | (0.58, 0.30, 0.66) | (0.50, 0.38, 0.60) | (0.33, 0.50, 0.59) |
| 旋转双曲面腔 | (0.49, 0.15, 0.74) | (0.58, 0.30, 0.71) | (0.60, 0.38, 0.78) | (0.65, 0.50, 0.79) |
| 旋转椭球面腔(主涡) | (0.66, 0.30, 0.48) | (0.66, 0.38, 0.86) | (0.93, 0.50, 0.88) | |
| 旋转椭球面腔(次涡) | (0.65, 0.30, 0.81) | (0.87, 0.38, 0.79) | ||
| 半球腔(主涡) | (0.53, 0.15, 0.39) | (0.49, 0.30, 0.53) | (0.49, 0.38, 0.53) | (0.92, 0.50, 0.93) |
| 半球腔(次涡) | (0.59, 0.38, 0.73) | |||
| “圆柱+半球”腔(主涡) | (0.67, 0.15, 0.49) | (0.56, 0.30, 0.44) | (0.56, 0.38, 0.42) | (0.30, 0.50, 0.74) |
| “圆柱+半球”腔(次涡) | (0.36, 0.38, 0.75) | (0.90, 0.50, 0.92) | ||
| “长方体+半圆柱”腔 | (0.60, 0.15, 0.72) | (0.51, 0.30, 0.54) | (0.51, 0.38, 0.42) | (0.51, 0.50, 0.39) |
Table 3 Distribution of the vortex center of different cavities along y-direction
| 腔体形状 | y/Ymax= 0.15 | y/Ymax= 0.3 | y/Ymax= 0.38 | y/Ymax= 0.5 |
| 长方体腔 | (0.77, 0.15, 0.55) | (0.68, 0.30, 0.58) | (0.59, 0.38, 0.58) | (0.54, 0.50, 0.58) |
| 圆柱腔 | (0.70, 0.15, 0.62) | (0.65, 0.30, 0.45) | (0.33, 0.38, 0.41) | (0.25, 0.50, 0.38) |
| 半圆柱腔 | (0.70, 0.15, 0.52) | (0.58, 0.30, 0.66) | (0.50, 0.38, 0.60) | (0.33, 0.50, 0.59) |
| 旋转双曲面腔 | (0.49, 0.15, 0.74) | (0.58, 0.30, 0.71) | (0.60, 0.38, 0.78) | (0.65, 0.50, 0.79) |
| 旋转椭球面腔(主涡) | (0.66, 0.30, 0.48) | (0.66, 0.38, 0.86) | (0.93, 0.50, 0.88) | |
| 旋转椭球面腔(次涡) | (0.65, 0.30, 0.81) | (0.87, 0.38, 0.79) | ||
| 半球腔(主涡) | (0.53, 0.15, 0.39) | (0.49, 0.30, 0.53) | (0.49, 0.38, 0.53) | (0.92, 0.50, 0.93) |
| 半球腔(次涡) | (0.59, 0.38, 0.73) | |||
| “圆柱+半球”腔(主涡) | (0.67, 0.15, 0.49) | (0.56, 0.30, 0.44) | (0.56, 0.38, 0.42) | (0.30, 0.50, 0.74) |
| “圆柱+半球”腔(次涡) | (0.36, 0.38, 0.75) | (0.90, 0.50, 0.92) | ||
| “长方体+半圆柱”腔 | (0.60, 0.15, 0.72) | (0.51, 0.30, 0.54) | (0.51, 0.38, 0.42) | (0.51, 0.50, 0.39) |
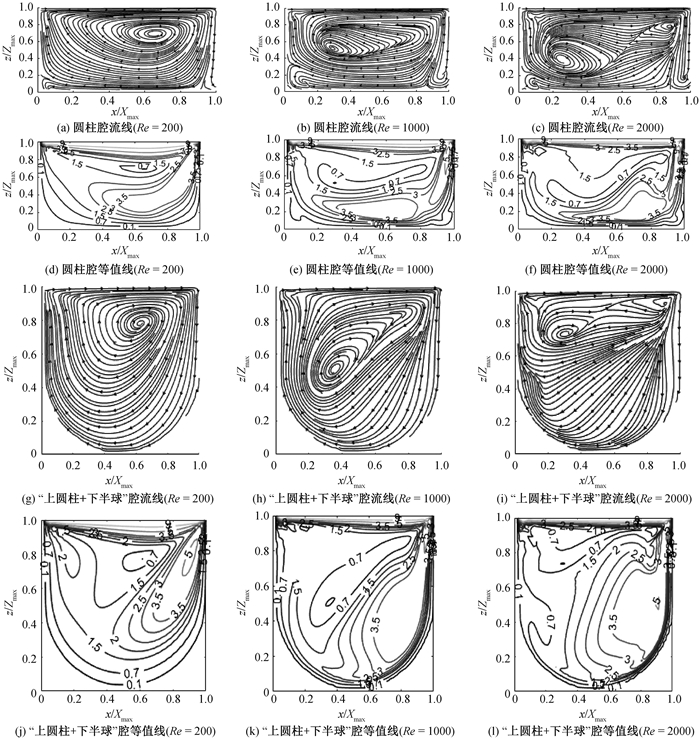
Fig.9 Streamlines and velocity countours on vertical sections of a cylindrical cavity and a cavity with cylinderup hemisphere at different Reynolds numbers
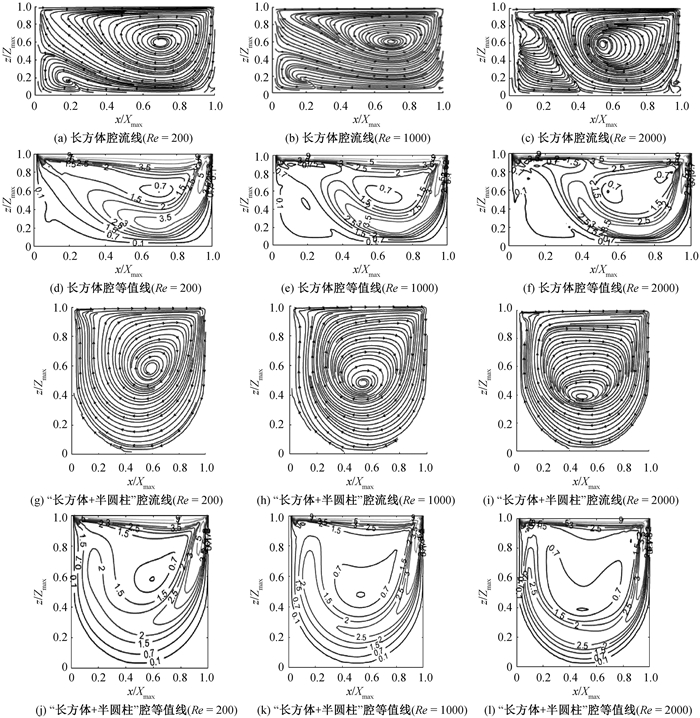
Fig.10 Streamlines and velocity countours on the central vertical section of a square cavity and a cavity with cuboid upsemi-cylinder at different Reynolds numbers
| 1 |
CHANG L. Experimental study of the three-dimensional lid-drive cavity flow of the high Reynolds number[D]. Tianjin: Tianjin University, 2014.
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
DOI |
| 8 |
|
| 9 |
|
| 10 |
DOI |
| 11 |
DOI |
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
DOI |
| 16 |
DOI |
| 17 |
DOI |
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| [1] | Shuting FENG, Houping DAI, Tongzheng SONG. Lattice Boltzmann Method for Two-dimensional Fractional Reaction-Diffusion Equations [J]. Chinese Journal of Computational Physics, 2022, 39(6): 666-676. |
| [2] | Liubin ZHANG, Yanguang SHAN, Zhicheng RONG. Single Bubble Dynamics in Pool Boiling Under Uniform Electric Field: LBM Simulation [J]. Chinese Journal of Computational Physics, 2022, 39(5): 537-548. |
| [3] | Jiaxin LIU, Lin ZHENG, Beihao ZHANG. Entropy Generation in Double-diffusive Natural Convection in a Square Porous Enclosure: Lattice Boltzmann Method [J]. Chinese Journal of Computational Physics, 2022, 39(5): 549-563. |
| [4] | Pin-liang LIN, Huan-huan FENG, Yu-hong DONG. Analysis of Flow Field Around a Cylinder with Porous Media Layer [J]. Chinese Journal of Computational Physics, 2022, 39(4): 418-426. |
| [5] | Lu CHEN, Ming GAO, Jia LIANG, Dongmin WANG, Yugang ZHAO, Lixin ZHANG. Droplet Upward Movement on an Inclined Surface Under Wetting Gradient: Lattice Boltzmann Simulation [J]. Chinese Journal of Computational Physics, 2021, 38(6): 672-682. |
| [6] | Xuedan WEI, Houping DAI, Mengjun LI, Zhoushun ZHENG. Lattice Boltzmann Method for One-dimensional Riesz Spatial Fractional Convection-Diffusion Equations [J]. Chinese Journal of Computational Physics, 2021, 38(6): 683-692. |
| [7] | Jiangtao ZHENG, Ninghong JIA, Huifang HU, Yong YANG, Yang JU, Moran WANG. Study on Liquid-Liquid Spontaneous Imbibition Dynamics in Bifurcated Channels [J]. Chinese Journal of Computational Physics, 2021, 38(5): 543-554. |
| [8] | Qin LOU, Sheng TANG, Haoyuan WANG. Numerical Simulation of Bubble Dynamics in Porous Media with a Lattice Boltzmann Large Density Ratio Model [J]. Chinese Journal of Computational Physics, 2021, 38(3): 289-300. |
| [9] | Jia LIANG, Ming GAO, Lu CHEN, Dongmin WANG, Lixin ZHANG. Lattice Boltzmann Study of a Droplet Impinging on a Stationary Droplet on a Fixed Wall Surface with Different Wettability [J]. Chinese Journal of Computational Physics, 2021, 38(3): 313-323. |
| [10] | YUAN Junjie, YE Xin, SHAN Yanguang. Natural Convection in Triangular Cavity Filled with Nanofluid: Lattice Boltzmann Simulation [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2021, 38(1): 57-68. |
| [11] | ZHAO Ming, WANG Ke, YU Duanmin. Ruelle-Takens Chaotic Natural Convection in a Horizontal Annulus with an Internally Slotted Circle [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(6): 667-676. |
| [12] | WANG Jianyi, PAN Zhenhai, WU Huiying. Numerical Study of Inertial Focusing Behavior of Ellipsoidal Particles in a Microchannel [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(6): 677-686. |
| [13] | ZHAN Jiemin, BIAN Shiqi, LUO Yingying, HU Wenqing, GONG Yejun. Periodicity Analysis and Benchmark Solution of Lid-driven Cavity at Re=15 000 [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(4): 413-421. |
| [14] | TANG Guyue, LOU Qin, LI Ling. Influence of Heating Size and Rayleigh Number on Natural Convection in a Deformable Open Cavity:Lattice Boltzmann Method [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(3): 263-276. |
| [15] | HU Yu, SUN Tao. Three-dimensional Numerical Simulation of Dynamics Characteristics of Two Rising Bubbles with Lattice Boltzmann Method [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(3): 277-283. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||
Copyright © Chinese Journal of Computational Physics
E-mail: jswl@iapcm.ac.cn
Supported by Beijing Magtech Co., Ltd.
