Magnetic Induction HR Neuron with Hidden Extreme Multistability and Its Circuit Implementation

doi:10.19596/j.cnki.1001-246x.8476

Abstract

Abstract:

With a magnetically controlled memristor to describe the coupling between membrane potential and magnetic flux, a magnetic induction HR neuron model is established. Its complex dynamical behavior is revealed with dynamic analysis methods including bifurcation diagrams, Lyapunov exponent spectrum, time sequences, and phase plots. It shows that the magnetic induction HR neuron has no equilibrium points while it can generate infinite hidden chaotic attractors with same topologies and different positions. Namely, the neuron model has the characteristic of hidden extreme multistability. Moreover, an analog equivalent circuit of the magnetic induction HR neuron is designed. Numerical simulations is verified with PSIM circuit simulations.

Key words: HR neuron, memristor, hidden attractors, extreme multistability, neuron circuit

Lihong TANG, Zongmei HE, Yanli YAO. Magnetic Induction HR Neuron with Hidden Extreme Multistability and Its Circuit Implementation[J]. Chinese Journal of Computational Physics, 2022, 39(5): 589-597.

Figures/Tables 12

Fig.1 Phase plots of hidden attractors (a) x-y phase plane; (b) x-φ phase plane; (c) y-φ phase plane

Fig.2 Lyapunov exponents as functions of time

Fig.3 Dynamical distribution related to magnetic induction intensity k1(a) Bifrucation; (b) Lyapunov exponents

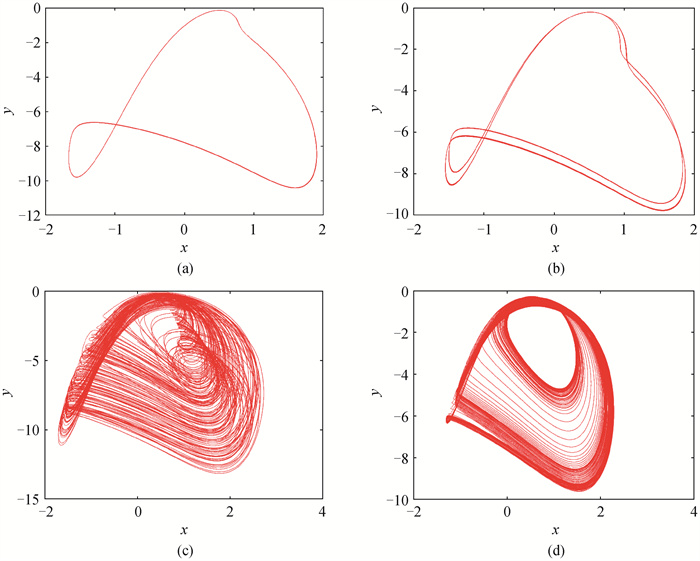
Fig.4 Phase plots of attractors corresponding to different magnetic induction intensity k1(a) Period-1 attractor at k1=-3.5; (b) Period-2 attractor at k1=-3; (c) Chaotic attractor at k1=-2.4; (d) Quasi-period attractor at k1=-1.8

Fig.5 Bifrucation diagram related to initial value φ(0)

Fig.6 Chaotic attractors related to initial value φ(0)

Fig.7 Periodic attractors related to initial value, from left to right, φ(0) = -18π, -16π, -14π, -12π, -10π, -8π, -6π, -4π, -2π, 0

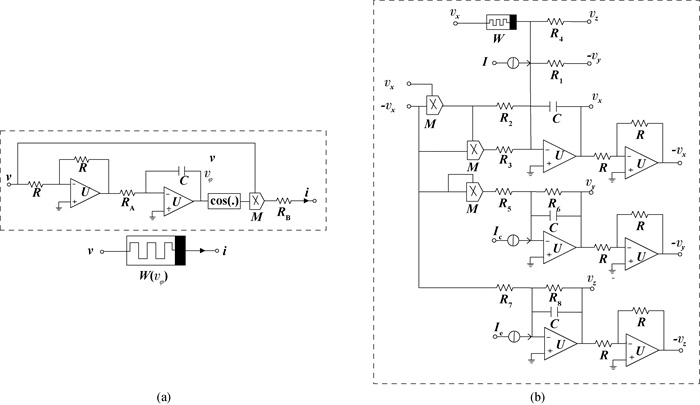
Fig.8 Magnetic induction HR neuron circuit (a) Analog equivalent circuit of cosin memristor; (b) Analog equivalent circuit of magnetic induction HR neuron

Fig.9 PSIM simulation circuit of magnetic induction HR neuron

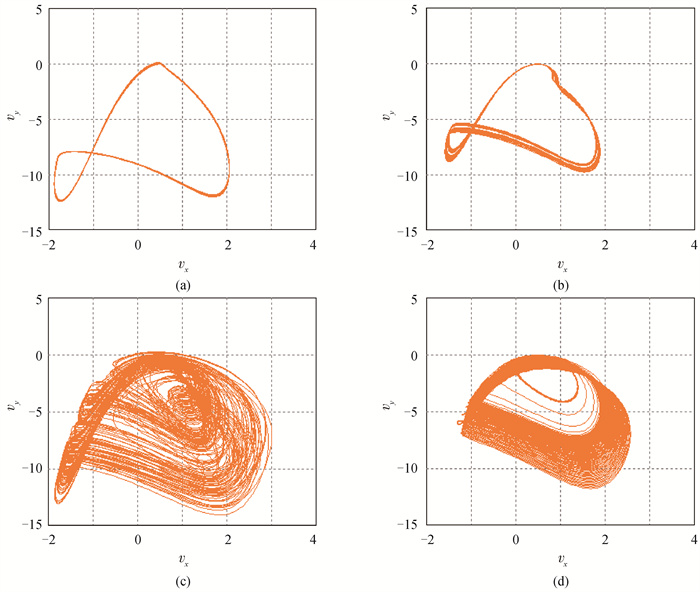
Fig.10 Chaotic attractors generated by magnetic induction HR neuron circuit with RB=4 kΩ (k1= -2.5) (a) vx- vy phase plane; (b) vx- vφ phase plane

Fig.11 Phase plot of attractors generated by magnetic induction HR neuron circuit under different magnetic induction intensities (a) Period attractor with RB=2.86 kΩ (k1=-3.5); (b) Period attractor with RB=3.4 kΩ (k1=-3); (c) Chaotic attractor with RB=4 kΩ (k1=-2.4); (d) Transient chaotic attractor with RB=5.55 kΩ (k1=-1.8)

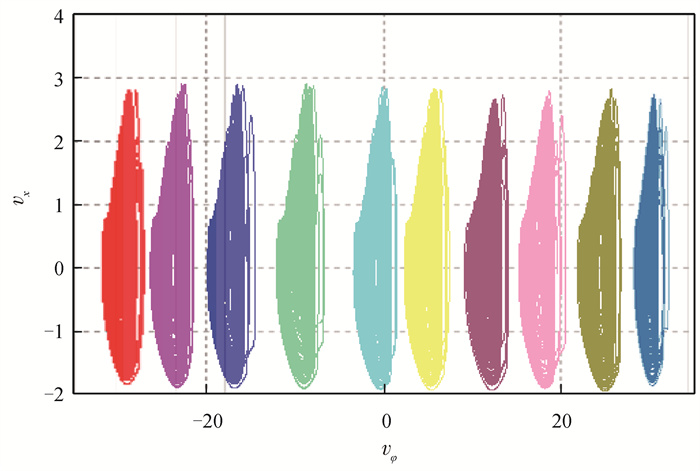
Fig.12 Chaotic attractors generated by magnetic induction HR neuron circuit under different initial voltages, from left to right, vz = -26π, -24π, -22π, -20π, -18π, -16π, -14π, -12π, -10π, -8π

References 27

1	陈墨, 陈成杰, 包伯成, 等. 忆阻突触耦合Hopfield神经网络的初值敏感动力学[J]. 电子与信息学报, 2020, 42 (4): 870- 877.
2	TANG L H , HE Z M , YAO Y L . Dynamical analysis and circuit implementation of a memristive Hopfield neural network[J]. Chinese Journal of Computational Physics, 2022, 39 (2): 244- 252.
3	HODGKIN A L , HUXLEY A F . A quantitative description of membrane current and its application to conduction and excitation in nerve[J]. The Journal of Physiology, 1952, 117 (4): 500- 544. DOI
4	FITZHUGH R . Impulses and physiological states in theoretical models of nerve membrane[J]. Biophysical Journal, 1961, 1 (6): 445- 466. DOI
5	王国威, 付燕. 电磁场作用下FHN神经元模型的动力学性质[J]. 湖北理工学院学报, 2021, 37 (2): 53- 58. DOI
6	HINDMARSH J L , ROSE R M . A model of the nerve impulse using two first-order differential equations[J]. Nature, 1982, 296 (5853): 162- 164. DOI
7	乔帅, 安新磊, 王红梅, 等. 磁通e-HR神经元隐藏放电与分岔行为的研究[J]. 云南大学学报(自然科学版), 2020, 42 (4): 685- 694.
8	安新磊, 张莉. 一类忆阻神经元的电活动多模振荡及Hamilton能量反馈控制[J]. 力学学报, 2020, 52 (4): 1174- 1188.
9	王松, 茅晓晨. 含时滞的忆阻耦合HR神经元的复杂放电行为[J]. 动力学与控制学报, 2020, 18 (1): 33- 39.
10	LV M , MA J . Multiple modes of electrical activities in a new neuron model under electromagnetic radiation[J]. Neurocomputing, 2016, 205, 375- 381.
11	BAO H , LIU W , HU A . Coexisting multiple firing patterns in two adjacent neurons coupled by memristive electromagnetic induction[J]. Nonlinear Dynamics, 2019, 95 (1): 43- 56.
12	王红梅, 安新磊, 乔帅, 等. 磁通e-HR神经元模型的Hopf分岔分析与控制[J]. 山东理工大学学报(自然科学版), 2020, 34 (4): 50- 56. 50-56+62
13	安新磊, 乔帅, 张莉. 基于麦克斯韦电磁场理论的神经元动力学响应与隐藏放电控制[J]. 物理学报, 2021, 70 (5): 46- 65.
14	STRUKOV D , SNIDER G , STEWART D , et al. The missing memristor found[J]. Nature, 2008, 453 (7191): 80- 83.
15	王春华, 蔺海荣, 孙晶如, 等. 基于忆阻器的混沌、存储器及神经网络电路研究进展[J]. 电子与信息学报, 2020, 42 (4): 795- 810.
16	BAO B , HU A , BAO H , et al. Three-dimensional memristive Hindmarsh-Rose neuron model with hidden coexisting asymmetric behaviors[J]. Complexity, 2018, 3872573, 1- 12.
17	BAO H , HU A , LIU W , et al. Hidden bursting firings and bifurcation mechanisms in memristive neuron model with threshold electromagnetic induction[J]. IEEE transactions on neural networks and learning systems, 2020, 31 (2): 502- 511.
18	LIN H , WANG C , SUN Y , et al. Firing multistability in a locally active memristive neuron model[J]. Nonlinear Dynamics, 2020, 100 (4): 3667- 3683.
19	LAI Q , KUATE P D K , LIU F , et al. An extremely simple chaotic system with infinitely many coexisting attractors[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2020, 67 (6): 1129- 1133.
20	徐昌彪, 何颖辉, 吴霞, 等. 多种多翼吸引子共存的新型三维分数阶混沌系统[J]. 哈尔滨工业大学学报, 2020, 52 (5): 92- 98.
21	BAO H , LIU W , MA J , et al. Memristor initial-offset boosting in memristive HR neuron model with hidden firing patterns[J]. International Journal of Bifurcation and Chaos, 2020, 30 (10): 2030029.
22	MA J , TANG J . A review for dynamics in neuron and neuronal network[J]. Nonlinear Dynamics, 2017, 89 (3): 1569- 1578.
23	TAKEMBO C N , MVOGO A , FOUDA H P , et al. Modulated wave formation in myocardial cells under electromagnetic radiation[J]. International Journal of Modern Physics B, 2018, 32 (14): 1850165.
24	BAO H , CHEN M , WU H G , et al. Memristor initial-boosted coexisting plane bifurcations and its extreme multi-stability reconstitution in two-memristor-based dynamical system[J]. Science China Technological Sciences, 2020, 63 (4): 603- 613.
25	XUE W , ZHANG Y . Application of conservative hyperchaos in digital image encryption[J]. Chinese Journal of Computational Physics, 2020, 37 (4): 497- 504.
26	ZHAO M , WANG K , YU D . Ruelle-Takens chaotic natural convection in a horizontal annulus with an internally slotted circle[J]. Chinese Journal of Computational Physics, 2020, 37 (6): 667- 676.
27	SHI J , LI P , LIU G . Synchronization control and parameter identification for unified chaotic system based on improved clonal selection algorithm[J]. Chinese Journal of Computational Physics, 2020, 37 (2): 240- 252.

[1]	Lihong TANG, Zongmei HE, Yanli YAO. Dynamical Analysis and Circuit Implementation of a Memristive Hopfield Neural Network [J]. Chinese Journal of Computational Physics, 2022, 39(2): 244-252.
[2]	Jia LUO, Liang SUN, Yinhu QIAO. Dynamical Analysis and Circuit Implementation of a Memristor Synapse-coupled Ring Hopfield Neural Network [J]. Chinese Journal of Computational Physics, 2022, 39(1): 109-117.
[3]	WANG Wei, ZENG Yicheng, CHEN Zheng, SUN Ruiting. Coexisting Attractors and Hopf Bifurcation in Floating Memristors Based Chaotic Circuit [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2017, 34(6): 747-756.
[4]	YU Shicheng, ZENG Yicheng, LI Zhijun. A Quadratic Memristor-based Fourth-order Chaotic Circuit [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2015, 32(6): 735-743.
[5]	TAN Zhiping, YANG Hongjiao, LIU Qineng, ZENG Yicheng. Analysis and Implementation of a Simplest Charge-controlled Memristor Chaotic Circuit [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2015, 32(4): 496-504.