Propagation of Nanoscale Microcrack Under Disturbance Strain at Different Temperatures: Phase-Field-Crystal Model

doi:10.19596/j.cnki.1001-246x.8509

Abstract

Abstract:

A phase-field-crystal model is used to simulate microcrack growth under disturbance strain. Influences of disturbance frequency and temperature on growth behavior and stability of microcrack are discussed. It shows that: ① Fracture mode is affected by temperature of the system under certain conditions. ② Influence of disturbance frequency on crack propagation behavior is affected by temperature of the system. ③ Stability of crack decreases firstly and then increases with the increase of disturbance frequency. The increase of temperature leads to the decrease of crack stability.

Key words: phase-field-crystal, disturbance strain, temperature, microcrack

Jianwei LI, Xuan XIANG, Jingdong WANG, Shi HU, Zheng CHEN, Yuanhua HE. Propagation of Nanoscale Microcrack Under Disturbance Strain at Different Temperatures: Phase-Field-Crystal Model[J]. Chinese Journal of Computational Physics, 2022, 39(6): 717-726.

Figures/Tables 7

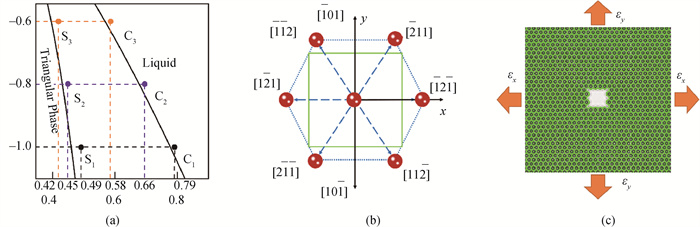
Fig.1 (a) Two-dimensional phase diagram calculated with one-mode approximation; (b) A schematic of the orientation between the crack and the lattice (The blue hexagon box signifies the triangular lattice. The green square box indicates the crack. The dimensions are relatively adjusted to facilitate analysis.); (c) illustration of the initial simulation system(Green and white regions indicate triangular lattice and central crack, respectively.)

Table 1 Parameters of the simulation systems

体系	温度r	频率ω /(10^-5Δt^-1)	体系	温度r	频率ω /(10^-5Δt^-1)	体系	温度r	频率ω /(10^-5Δt^-1)
A₁	-1.0	无扰动	A₂	-0.8	无扰动	A₃	-0.6	无扰动
B₁	-1.0	0.2	B₂	-0.8	0.2	B₃	-0.6	0.2
C₁	-1.0	2	C₂	-0.8	2	C₃	-0.6	2
D₁	-1.0	20	D₂	-0.8	20	D₃	-0.6	20
E₁	-1.0	200	E₂	-0.8	200	E₃	-0.6	200
F₁	-1.0	2 000	F₂	-0.8	2 000	F₃	-0.6	2 000

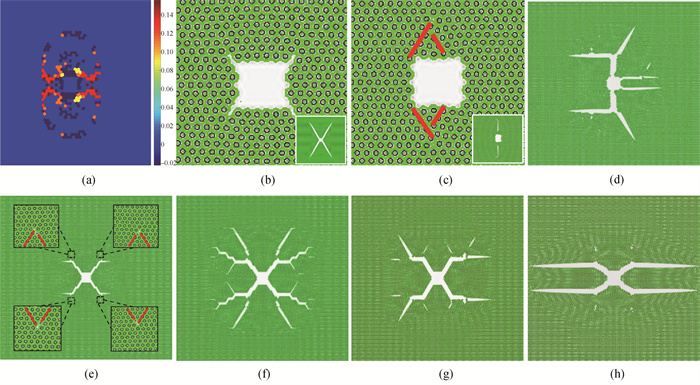
Fig.2 (a) Strain distribution pattern of system A1 at n = 27 000; (b) Morphology of system A1 at n = 27 000 (The inset is a local morphology around the central crack at n = 60 000.); (c) Morphology of system C1 at n = 13 000 (The inset is a local morphology around the central crack at n = 40 000.); (d) Morphology of system C1 at n = 57 000; (e) Morphology of system D1 at n = 45 000; (f) Morphology of system D1 at n = 60 000; (g) Morphology of system E1 at n = 60 000; (h) Morphology of system F1 at n = 67 000 (The extra half planes of atoms are indicated by the red lines.)

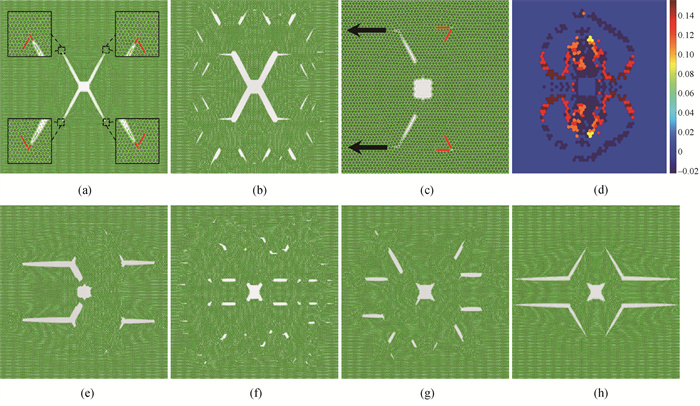
Fig.3 (a) Morphology of system B2 at n = 38 000 (The red lines indicate extra half planes of atoms.); (b) Morphology of system B2 at n = 55 000; (c) Morphology of system C2 at n = 30 000 (The black arrows indicate crack propagation direction.); (d) Strain distribution pattern of system C2 at n = 18 000; (e) Morphology of system C2 at n = 57 000; (f) Morphology of system D2 at n = 60 000; (g) Morphology of system E2 at n = 60 000; (h) Morphology of system F2 at n = 60 000

Fig.4 (a) Morphology of system A3 at n = 50 000; (b) Morphology of system B3 at n = 43 000; (c) Morphology of system C3 at n = 49 000; (d) Morphology of system D3 at n = 51 000; (e) Morphology of system E3 at n = 50 000; (f) Morphology of system F3 at n = 51 000

Table 2 Crack propagation modes of simulated systems

体系	裂纹扩展模式	体系	裂纹扩展模式	体系	裂纹扩展模式
A₁	脆性扩展	A₂	脆性扩展	A₃	韧性扩展
B₁	脆性扩展	B₂	韧性扩展	B₃	韧性扩展
C₁	韧性扩展	C₂	韧性扩展	C₃	韧性扩展
D₁	韧性扩展	D₂	韧性扩展	D₃	韧性扩展
E₁	韧性扩展	E₂	韧性扩展	E₃	韧性扩展
F₁	韧性扩展	F₂	韧性扩展	F₃	韧性扩展

Fig.5 Time step number at which the central crack beginning to lose stability under different disturbance frequencies and system temperatures

References 28

1	NAM K H . Molecular dynamics: From small molecules to macromolecules[J]. International Journal of Molecular Sciences, 2021, 22 (7): 3761. DOI
2	LIANG Hua , LI Maosheng . Molecular dynamics study of mechanical properties of single crystal aluminum with voids and vacancies[J]. Chinese Journal of Computational Physics, 2019, 36 (2): 211- 218.
3	LI Qi , LI Xi , YANG Xiaofeng , et al. Highly efficient and linear numerical schemes with unconditional energy stability for the anisotropic phase-field crystal model[J]. Journal of Computational and Applied Mathematics, 2021, 383 (11): 113122.
4	FENG Qihong , ZHAO Yunchang , WANG Sen , et al. Pore-scale oil-water two-phase flow simulation based on phase field method[J]. Chinese Journal of Computational Physics, 2020, 37 (4): 439- 447.
5	HAGHANI-HASSAN-ABADI R , FAKHARI A , RAHIMIAN M H . Phase-change modeling based on a novel conservative phase-field method[J]. Journal of Computational Physics, 2021, 432 (11): 110111.
6	ELDER K R , KATAKOWSKI M , HAATAJA M , et al. Modeling elasticity in crystal growth[J]. Physical Review Letters, 2002, 88 (24): 245701. DOI
7	WANG Xuemei , DONG Bin , ZHU Ziliang , et al. Interfacial interaction and diffusion properties of functionalized CNT/polymer systems: Molecular dynamics simulations[J]. Chinese Journal of Computational Physics, 2020, 37 (5): 589- 594.
8	陈成, 陈铮, 杨涛, 等. 晶体相场模型的研究进展[J]. 材料导报, 2012, 26 (9): 116- 119. 116-119, 141
9	BERRY J , GRANT M , ELDER K R . Diffusive atomistic dynamics of edge dislocations in two dimensions[J]. Physical Review E, 2006, 73 (3 Pt 1): 031609.
10	HU Shi , CHEN Zheng , YU Genggeng , et al. Phase-field-crystal study on the reaction mechanisms of opposite sign edge dislocations appearing in the deformation processes of asymmetric tilt sub-grain boundary system[J]. Computational Materials Science, 2016, 124 (7): 195- 203.
11	BERRY J , PROVATAS N , ROTTLER J , et al. Defect stability in phase-field crystal models: Stacking faults and partial dislocations[J]. Physical Review B: Condensed Matter & Materials Physics, 2012, 86 (22): 224112.
12	YAMANAKA A , MCREYNOLDS K , VOORHEES P W . Phase field crystal simulation of grain boundary motion, grain rotation and dislocation reactions in a BCC bicrystal[J]. Acta Materialia, 2017, 133 (5): 160- 171.
13	吴璐, 潘荣剑, 张伟, 等. 双模晶体相场研究六方四方相变过程晶界和位错演化[J]. 稀有金属材料与工程, 2020, 49 (12): 4103- 4111.
14	GREENWOOD M , OFORI-OPOKU N , ROTTLER J , et al. Modeling structural transformations in binary alloys with phase field crystals[J]. Physical Review B, 2011, 84 (6): 064104. DOI
15	BALAKRISHNA A R , CARTER W C . Combining phase-field crystal methods with a Cahn-Hilliard model for binary alloys[J]. Physical Review E, 2018, 97 (4): 043304. DOI
16	TIAN Xiaolin , ZHAO Yuhong , PENG Dunwei , et al. Phase-field crystal simulation of evolution of liquid pools in grain boundary pre-melting regions[J]. Transactions of Nonferrous Metals Society of China, 2021, 31 (4): 1175- 1188. DOI
17	赵宇龙, 陈铮, 龙建, 等. 晶体相场法模拟纳米晶材料反霍尔-佩奇效应的微观变形机理[J]. 物理学报, 2013, 62 (11): 118102.
18	马文婧, 柯常波, 周敏波, 等. Sn/Cu互连体系界面和金属间化合物层Kirkendall空洞演化和生长动力学的晶体相场法模拟[J]. 金属学报, 2015, 51 (7): 873- 882.
19	ELDER K R , THOMTON K , HOYT J J . The Kirkendall effect in the phase field crystal model[J]. Philosophical Magazine, 2011, 91 (1): 151- 164. DOI
20	卢艳丽, 卢广明, 胡婷婷, 等. 晶体相场法研究Kirkendall效应诱发的相界空洞的形成和演变[J]. 金属学报, 2015, 51 (7): 866- 872.
21	HU Shi , XI Wen , CHEN Zheng , et al. Coupled motion of grain boundaries and the influence of microcracks: A phase-field-crystal study[J]. Computational Materials Science, 2017, 132 (2): 125- 131.
22	郭刘洋, 陈铮, 龙建, 等. 晶体相场法研究应力状态及晶体取向对微裂纹尖端扩展行为的影响[J]. 物理学报, 2015, 64 (17): 178102.
23	LU Yujiang , GAO Yingjun , DENG Qianqian , et al. Effect of crystal orientation on initiation and propagation of crack: Phase field crystal model study[J]. The European Physical Journal B: Condensed Matter and Complex Systems, 2019, 92 (9): 1- 10.
24	LIU Zheyuan , GAO Yingjun , DENG Qianqian , et al. A nanoscale study of nucleation and propagation of Zener types cracks at dislocations: Phase field crystal model[J]. Computational Materials Science, 2020, 179 (10): 109640.
25	HU Shi . Phase-field-crystal study on deformation behavior of nanoscale monocrack system in the ductile-to-brittle transition region[J]. Fatigue & Fracture of Engineering Materials & Structures, 2020, 43 (1): 63- 76.
26	HU Shi , LI Jianwei , LIU Quanyi , et al. Phase-field-crystal study on the crack propagation behavior in a nanoscale two-dimensional lattice in the presence of nonlinear disturbance strains[J]. Fatigue & Fracture of Engineering Materials & Structures, 2021, 44 (10): 2706- 2717.
27	HARREN S V , ASARO R J . Nonuniform deformations in polycrystals and aspects of the validity of the Taylor model[J]. Journal of the Mechanics & Physics of Solids, 1989, 37 (3): 191- 232.
28	NABARRO F . Fifty-year study of the Peierls-Nabarro stress[J]. Materials Science & Engineering A, 1997, 234, 67- 76.

[1]	Hong LI, Lixin ZHANG, Yan REN, Ming GAO, Jingnan LIU. Prediction of Water Temperature of Mixed-flow Closed Cooling Tower Based on BP Neural Network and Grey Correlation Analysis [J]. Chinese Journal of Computational Physics, 2022, 39(1): 53-59.
[2]	Zhankang YANG, Yi NIU. Influence of Temperature, Enclosure and Ventilation on Radon Concentration Distribution in a Blind Roadway [J]. Chinese Journal of Computational Physics, 2021, 38(4): 456-464.
[3]	CHE Yanjin, QI Yingxia, PAN Shuai, WANG Yuhe, ZHANG Hua. Microscopic Mechanism of Nonlinear Gas Alternating Oscillation in Microchannel Pulse Tube: Molecular Dynamics Study [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(5): 571-580.
[4]	CHEN Yu, XING Yongming. Effect of Hydrostatic Pressure on Magneto-optical Properties of Al₁₄Mn₂P₁₆: A Density Functional Theory Study [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(2): 231-239.
[5]	SU Geman, CUI Guomin, BAO Zhongkai, XIAO Yuan, CEN Zhenyu. Analysis and Treatment on Structures with Temperature Cross in Heat Exchanger Network [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(1): 107-118.
[6]	HE Yunlong, LI Ling. Heat Transfer and Phase Change of Laser Irradiated Gold Particle with Scattering Effect [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2019, 36(2): 182-188.
[7]	LIU Yongqiang, ZHA Xuejun, WANG Qingsong, YANG Zhen, XIA Qinghao, WU Bin. Influence of Local Heat Source on Thermal Transport in Magnetic Island [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2019, 36(2): 203-210.
[8]	ZHANG Kesheng, ZHANG Xiangqun, SHAO Fang, TANG Wenyong. Analysis of Environmental Influencing on Acoustic Relaxation Frequency in Multi-component Excitable Gases [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2019, 36(1): 89-98.
[9]	LI Xixia, WANG Li, DAI Haiyan, LI Changyu. Non-Fourier Heat Transfer Based on Extended Separation Variable Method [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(6): 685-692.
[10]	QI Peng, LIU Huiqing, PANG Zhanxi, LIU Huapu, CHEN Yu. Temperature Distribution Modeling in SAGD Circulation Phase [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(1): 64-70.
[11]	LI Zhenhuan, SUN Haifeng, XIA Xinlin, LI Yang. Decoupling Method for Transient Thermal Status of Low Supersonic Aircrafts [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2016, 33(6): 681-690.
[12]	DAI Zihuan, WU Jiming, DING Ning. Artificial Viscosity Splitting Strategy in Lagrangian Algorithm for Two-dimensional Three-temperature Radiation Magnetohydrodynamics [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2015, 32(4): 379-385.
[13]	WANG Ran, AN Liansuo, SHEN Guoqing, ZHANG Shiping. Three-Dimensional Temperature Field Reconstruction with Acoustics Based on Regularized SVD Algorithm [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2015, 32(2): 195-201.
[14]	WANG Hongliang, TIAN Zhou, GUO Yonghui. Effect of Particles-piled on Energy Attenuation at High Temperature and High Pressure [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2014, 31(6): 706-712.
[15]	LI Bo, NING Bo, SU Haiyang, LIU Hong, WEI Yunsheng. A Calculation Method for Temperature and Pressure Distribution in Water Production Gas Wellbores [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2014, 31(5): 573-580.