Progress in Study of Equation of State of Warm Dense Matter with Path-integral Monte Carlo Method

doi:10.19596/j.cnki.1001-246x.8599

Abstract

Abstract:

In this paper, the basic framework of PIMC method is firstly described in detail. In particular, four techniques developed for PIMC simulations to deal with the Fermi sign problem are reviewed. EOS data of various WDM systems obtained with PIMC simulations are then summarized, with which the advantages and disadvantages of PIMC method are illustrated. Finally, some future prospects of PIMC method are discussed.

Key words: warm dense matter, equation of state, path-integral Monte Carlo

Zixiang YAN, Wei KANG, Weiyan ZHANG, Xiantu HE. Progress in Study of Equation of State of Warm Dense Matter with Path-integral Monte Carlo Method[J]. Chinese Journal of Computational Physics, 2023, 40(2): 258-274.

Figures/Tables 8

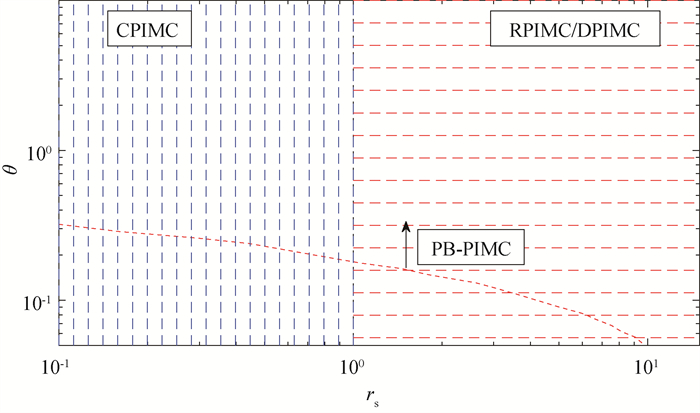
Fig.1 The ranges of applicability for different PIMC method in the study of UEG (The density parameter $ r_{\mathrm{s}}=a / a_0$ with a the average distance of electrons and a0 the Bohr radius, and the temperature parameter $\varTheta=T / T_{\mathrm{F}} $ with TF the Fermi temperature.)

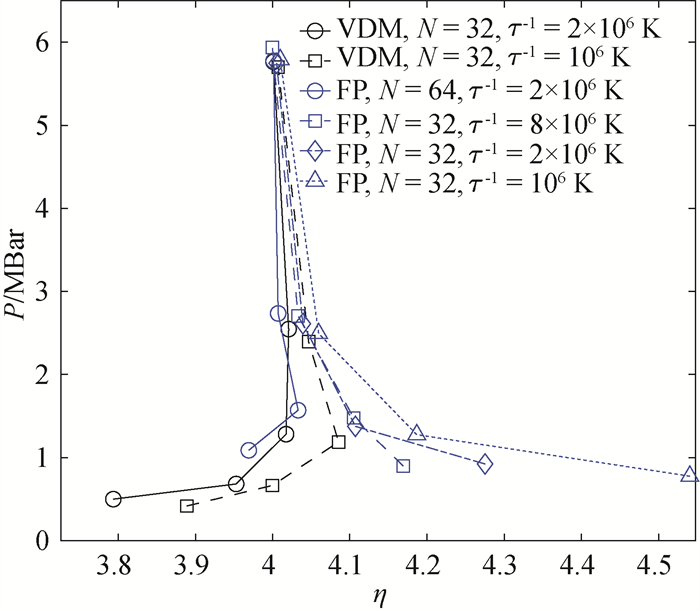
Fig.2 Hugoniot curve of deuterium calculated with RPIMC method[47] (Data points in different colors and marks represent the results calculated with different time steps τ, particle number N and nodal types.)

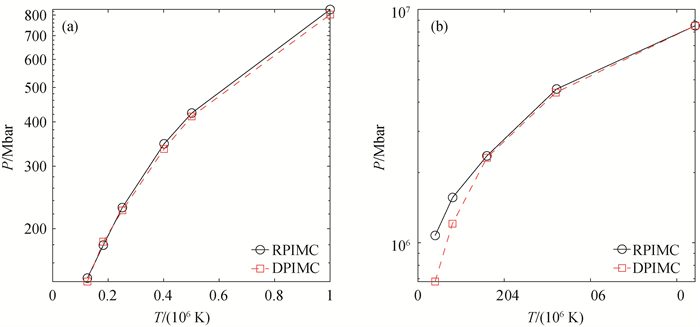
Fig.3 Temperature dependence of deuterium's pressure at constant density of (a) ρ = 10.00 g ·cm-3 and (b) ρ = 1 596.49 g ·cm-3 (The black circles stand for the RPIMC results[47], while the red squares represent the DPIMC results[46].)

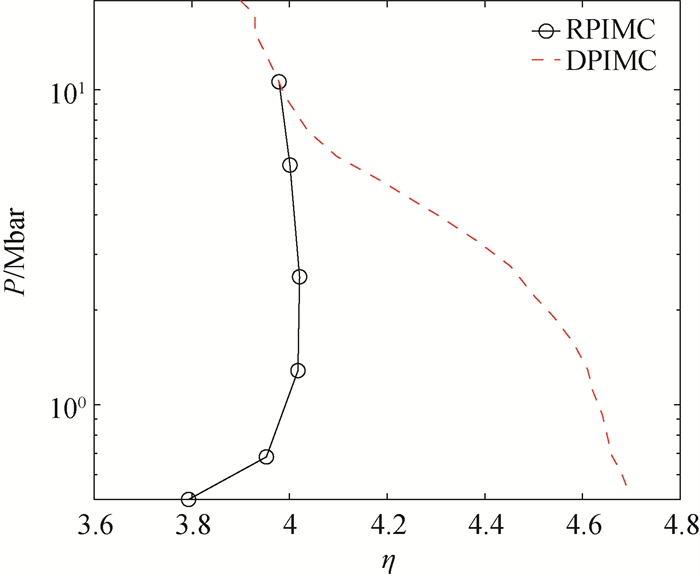
Fig.4 Hugoniot curve of deuterium calculated with DPIMC method[86], as represented by the red dashed curve. The results of RPIMC simulation[47] are also presented with the black curve, for the comparison purpose

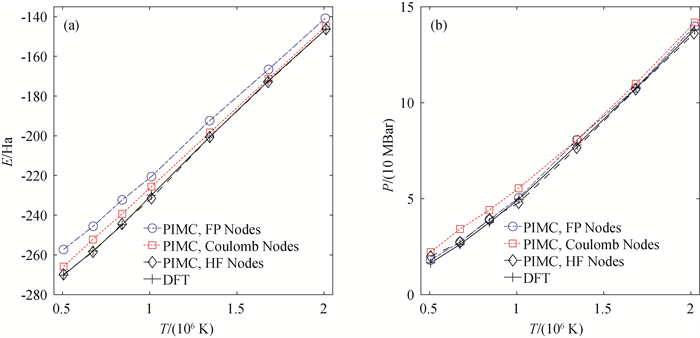
Fig.5 (a) Temperature dependence of internal energy of a single silicon atom[61] (Periodic cell of 5.0 Bohr is employed in simulation. The data points in different marks represent the results calculated with different nodes. The density functional theory (DFT) results are also shown as the reference, as represented by the black crosses.); (b) Temperature dependence of pressure of a single silicon atom

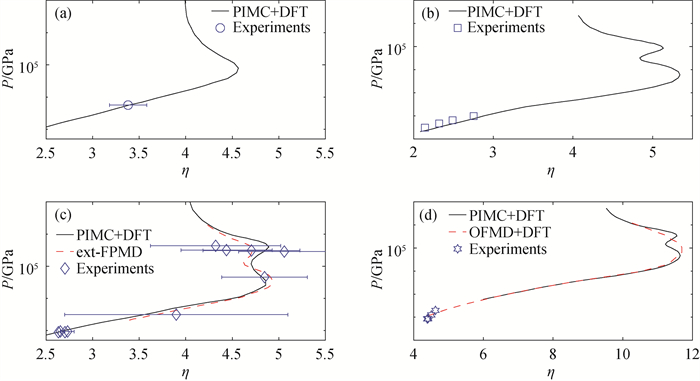
Fig.6 Hugoniot curves of middle Z materials. (a) Hugoniot curve of Boron (The black curve and blue circles represent the results of RPIMC+DFT-MD[51] and experiments[51].); (b) Hugoniot curve of Sodium (The black curve and blue squares represent the results of RPIMC+DFT-MD[57] and the experiments cited within Ref. [57].); (c) Hugoniot curve of Aluminum (The black curve, red dashed curve and blue squares represent the results of RPIMC+DFT-MD[60], ext-FPMD[23] and the experiments cited within Ref. [60].); (d) Hugoniot curve of Silicon (The black curve, red dashed curve and blue squares represent the results of RPIMC+DFT-MD[62], OFMD+DFT-MD[62] and the experiments cited within Ref. [62].)

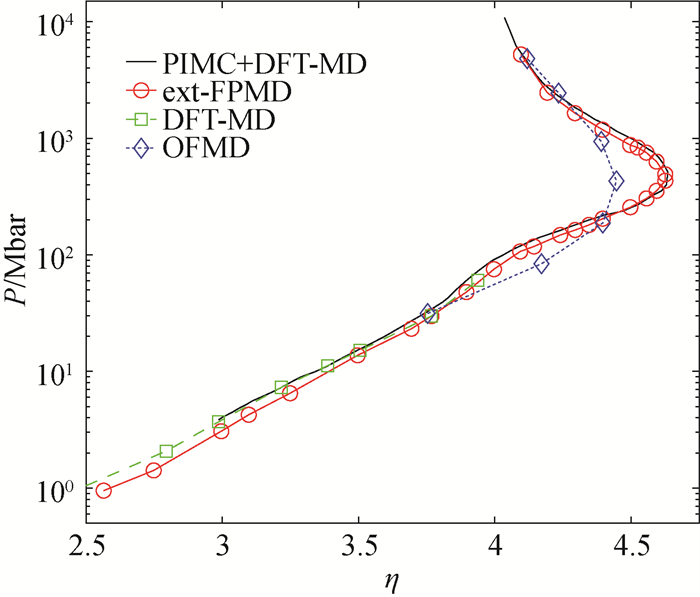
Fig.7 Hugoniot curve of Hydrocarbon (CH) (The black curve, red circles, green squares, and blue diamonds represent the results of RPIMC+DFT-MD[66], ext-FPMD[24], DFT-MD[88] and OFMD[88], respectively.)

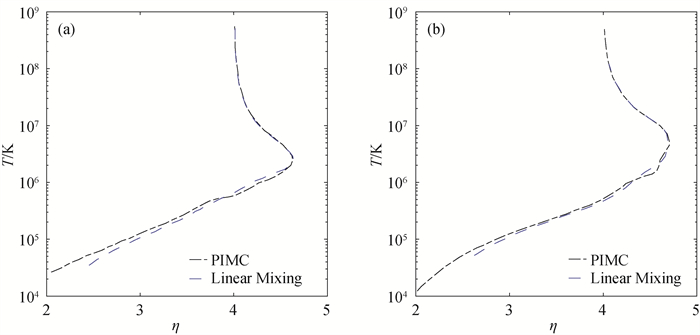
Fig.8 (a) Hugoniot curve of boron nitride (BN)[89] (The red curve represents the direct result of BN through RPIMC simulations with an initial density of 2.26g ·cm-3. The blue dash dot line represents the result with linear mixed approximation of elemental B and N.); (b) Hugoniot curve of magnesium silicate (MgSiO3)[89] (The red curve represents the RPIMC result of MgSiO3 with an initial density of 3.208 g ·cm-3, while the green dash dot curve represents the result with linear mixed approximation of elemental Mg, Si, and O.)

References 91

1	DRAKE R P . High-energy-density physics[M]. New York: Springer, 2006.
2	HE Xiantu , LI Jiwei , FAN Zhengfeng , et al. A hybrid-drive nonisobaric-ignition scheme for inertial confinement fusion[J]. Phys Plasmas, 2016, 23, 082706. DOI
3	LINDL J . Development of the indirect-drive approach to inertial confinement fusion and the target physics basis for ignition and gain[J]. Phys Plasmas, 1995, 2, 3933- 4024. DOI
4	CAMPBELL E , GONCHAROV V , SANGSTER T , et al. Laser-direct-drive program: Promise, challenge, and path forward[J]. Matter Radiat Extremes, 2017, 2, 37- 54. DOI
5	NILSEN J , KRITCHER A L , MARTIN M E , et al. Understanding the effects of radiative preheat and self-emission from shock heating on equation of state measurement at 100 s of Mbar using spherically converging shock waves in a NIF hohlraum[J]. Matter Radiat Extremes, 2020, 5, 018410.
6	FAN Zhengfeng , LIU Yuanyuan , LIU Bin , et al. Non-equilibrium between ions and electrons inside hot spots from National Ignition Facility experiments[J]. Matter Radiat Extremes, 2017, 2, 3- 8. DOI
7	YU Chengxin , FAN Zhengfeng , LIU Jie , et al. Modeling of shell-mixing into central hotspot in inertial confinement fusion implosion[J]. Chinese Journal of Computational Physics, 2017, 34 (4): 379- 386. DOI
8	HURRICANE O A , CALLAHAN D A , CASEY D T , et al. Fuel gain exceeding unity in an inertially confined fusion implosion[J]. Nature, 2014, 506, 343- 348. DOI
9	Gu Jianfa , GE Fengjun , DAI Zhensheng , et al. Influence of capsule support tent on ICF capsule implosion performance: Simulation study[J]. Chinese Journal of Computational Physics, 2020, 37 (6): 631- 638.
10	GIAMMICHELE N , CHARPINET S , FONTAINE G , et al. A large oxygen-dominated core from the seismic cartography of a pulsating white dwarf[J]. Nature, 2018, 554, 73- 76. DOI
11	ZEL'DOVICH Y B , RAIZER Y P . Physics of shock waves and high-temperature hydrodynamic phenomena[M]. New York and London: Academic Press, 1967.
12	KNUDSON M D , DESJARLAIS M P . High-precision shock wave measurements of deuterium: Evaluation of exchange-correlation functionals at the molecular-to-atomic transition[J]. Phys Rev Lett, 2017, 118, 035501. DOI
13	FERNANDEZ-PANELLA A , MILLOT M , FRATANDUONO D E , et al. Shock compression of liquid deuterium up to 1 TPa[J]. Phys Rev Lett, 2019, 122, 255702. DOI
14	MOSES E , BOYD R , REMINGTON B , et al. The National Ignition Facility: Ushering in a new age for high energy density science[J]. Phys Plasmas, 2009, 16, 041006. DOI
15	李儒新. 上海超强超短激光实验装置研制进展[J]. 强激光与粒子束, 2020, 32 (1): 011002.
16	NORA R , THEOBALD W , BETTI R , et al. Gigabar spherical shock generation on the OMEGA laser[J]. Phys Rev Lett, 2015, 114, 045001. DOI
17	HICKS D G , MEEZAN N B , DEWALD E L , et al. Implosion dynamics measurements at the National Ignition Facility[J]. Phys Plasma, 2012, 19, 122702. DOI
18	KRITCHER A L , SWIFT D C , DOPPNER T , et al. A measurement of the equation of state of carbon envelopes of white dwarfs[J]. Nature(London), 2020, 584, 51- 54. DOI
19	HOHENBERG P , KOHN W . Inhomogeneous electron gas[J]. Phys Rev, 1964, 136, B864- B870. DOI
20	KOHN W , SHAM L J . Self-consistent equations including exchange and correlation effects[J]. Phys Rev, 1965, 140, A1133- A1138. DOI
21	MERMIN N D . Thermal properties of the inhomogeneous electron gas[J]. Phys Rev, 1965, 137, A1441- A1443. DOI
22	WANG Cong , HE Xiantu , ZHANG Ping . Ab initio simulations of dense helium plasmas[J]. Phys Rev Lett, 2011, 106, 145002. DOI
23	ZHANG Shen , WANG Hongwei , KANG Wei , et al. Extended application of Kohn-Sham first-principles molecular dynamics method with plane wave approximation at high energy——From cold materials to hot dense plasmas[J]. Phys Plasmas, 2016, 23, 042707. DOI
24	LIU Xing , ZHANG Xiaohan , GAO Chang , et al. Equations of state of poly-α-methylstyrene and polystyrene: First-principles calculations versus precision measurements[J]. Phys Rev B, 2021, 103, 174111. DOI
25	KANG Dongdong , HOU Yong , ZENG Qiyu , et al. Unified first-principles equations of state of deuterium-tritium mixtures in the global inertial confinement fusion region[J]. Matter Radiat Extremes, 2020, 5, 055401. DOI
26	CEPERLEY D M . Path integrals in the theory of condensed helium[J]. Rev Mod Phys, 1995, 67, 279- 355. DOI
27	MILITZER B. Path integral Monte Carlo simulations of hot dense hydrogen[D]. Urbana, University of Illinois at Urbana-Champaign, 2000.
28	THOMAS L H . The calculation of atomic fields[J]. Proc Cambridge Philos Soc, 1927, 23, 542- 548. DOI
29	SWIFT D C , LOCKARD T , KRAUS R G , et al. Atom-in-jellium equations of state in the high-energy-density regime[J]. Phys Rev E, 2019, 99, 063210. DOI
30	LYON S P, JOHNSON J D. SESAME: The Los Alamos national laboratory equation of state database[R]. Group T-1, Report No. LA-UR-92-3407, Los Alamos Scientific Laboratory, 1992.
31	LIBERMAN D A . Self-consistent field model for condensed matter[J]. Phys Rev B, 1979, 20, 4981- 4989. DOI
32	WILSON B , SONNAD V , STERNE P , et al. Purgatorio-a new implementation of the inferno algorithm[J]. J Quant Spectrosc Radiat Transfer, 2012, 99, 658- 679.
33	MORE R , WARREN K , YOUNG D , et al. A new quotidian equation of state (QEOS) for hot dense matter[J]. Phys Fluids, 1988, 31, 3059- 3078. DOI
34	LIU Haifeng , SONG Haifeng , ZHANG Qili , et al. Validation for equation of state in wide regime: Copper as prototype[J]. Matter Radiat Extremes, 2016, 1, 123- 131. DOI
35	FEYNMAN R P , HIBBS A R . Quantum mechanics and path integrals[M]. New York: McGraw-Hill, 1965.
36	METROPOLIS N , ROSENBLUTH A W , ROSENBLUTH M N , et al. Equation of state calculations by fast computing machines[J]. J Chem Phys, 1953, 21, 1087- 1092. DOI
37	THIJSSEN J M . Computational physics[M]. Cambridge: Cambridge University, 2007.
38	POLLOCK E L , CEPERLEY D M . Simulation of quantum many-body systems by path-integral methods[J]. Phys Rev B, 1984, 30 (5): 2555- 2568. DOI
39	HERRERO C P . Dependence of the silicon lattice constant on isotopic mass[J]. Solid St Commun, 1999, 110, 243- 246. DOI
40	HERRERO C P , RAMIREZ R . Structural and thermodynamic properties of diamond: A path-integral Monte Carlo study[J]. Phys Rev B, 2001, 63, 024103.
41	ALLEN M P, TILDESLEY D J. Computer simulation of liquids[M]. Oxford, Clarendon press, 1989: 155-162.
42	NATOLI V , CEPERLEY D M . An optimized method for treating long-range potentials[J]. J Comput Phys, 1995, 117, 171- 178. DOI
43	MILITZER B . Computation of the high temperature Coulomb density matrix in periodic boundary conditions[J]. Comput Phys Commun, 2016, 204, 88- 96. DOI
44	CEPERLEY D M. Path-integral calculations of normal liquid ³He[J]. Phys Rev Lett, 69: 331-334.
45	FILINOV V S , FORTOV V E , BONITZ M , et al. Pair distribution functions of dense partially ionized hydrogen[J]. Phys Lett A, 2000, 274, 228- 235. DOI
46	ZHANG Qili , LIU Haifeng , LI Qiong , et al. Path integral Monte Carlo calculations of equation of state of hydrogen[J]. Chinese Journal of Computational Physics, 2019, 36 (4): 379- 385.
47	MILITZER B , CEPERLEY D M . Path integral Monte Carlo calculation of the deuterium Hugoniot[J]. Phys Rev Lett, 2000, 85, 1890- 1893. DOI
48	MILITZER B , CEPERLEY D M . Path integral Monte Carlo simulation of the low-density hydrogen plasma[J]. Phys Rev E, 2001, 63, 066404. DOI
49	MILITZER B . Path integral Monte Carlo and density functional molecular dynamics simulations of hot, dense helium[J]. Phys Rev B, 2009, 79, 155105. DOI
50	MILITZER B . First principles calculations of shock compressed fluid helium[J]. Phys Rev Lett, 2006, 97, 175501. DOI
51	ZHANG S , MILITZER B , GREGOR M C , et al. Theoretical and experimental investigation of the equation of state of boron plasmas[J]. Phys Rev E, 2018, 98, 023205. DOI
52	DRIVER K P , MILITZER B . All-electron path integral Monte Carlo simulations of warm dense matter: Application to water and carbon plasmas[J]. Phys Rev Lett, 2012, 108, 115502. DOI
53	BENEDICT L X , DRIVER K P , HAMEL S , et al. A multiphase equation of state for carbon addressing high pressures and temperatures[J]. Phys Rev B, 2014, 89, 224109. DOI
54	DRIVER K P , MILITZER B . First-principles equation of state calculations of warm dense nitrogen[J]. Phys Rev B, 2016, 93, 064101. DOI
55	DRIVER K P , SOUBIRAN F , ZHANG S , et al. First principles equation of state and electronic properties of warm dense oxygen[J]. J Chem Phys, 2015, 143, 164507. DOI
56	DRIVER K P , MILITZER B . First-principles simulations and shock Hugoniot calculations of warm dense neon[J]. Phys Rev B, 2015, 91, 045103. DOI
57	ZHANG S , DRIVER K P , SOUBIRAN F , et al. Equation of state and shock compression of warm dense sodium: A first principles study[J]. J Chem Phys, 2017, 146, 074505. DOI
58	ZHANG S , DRIVER K P , SOUBIRAN F , et al. Path integral Monte Carlo simulations of warm dense sodium[J]. High Energy Density Phys, 2016, 21, 16- 19. DOI
59	GONZÁLEZ-CATALDO F , SOUBIRAN F , MILITZER B . Equation of state of hot, dense magnesium derived with first-principles computer simulations[J]. Phys Plasmas, 2020, 27, 092706. DOI
60	DRIVER K P , SOUBIRAN F , MILITZER B . Path integral Monte Carlo simulations of warm dense aluminum[J]. Phys Rev E, 2018, 97, 063207. DOI
61	MILITZER B , DRIVER , K P . Development of path integral Monte Carlo simulations with localized nodal surfaces for second-row elements[J]. Phys Rev Lett., 2015, 115, 176403. DOI
62	HU S X , MILITZER B , COLLINS L A , et al. First-principles prediction of the softening of the silicon shock Hugoniot curve[J]. Phys Rev B, 2016, 94, 094109. DOI
63	DRIVER K P , MILITZER B . First-principles simulations of warm dense lithium fluoride[J]. Phys Rev E, 2017, 95, 043205. DOI
64	ZHANG S , MARSHALL M C , YANG L H , et al. Benchmarking boron carbide equation of state using computation and experiment[J]. Phys Rev E, 2020, 102, 053203. DOI
65	ZHANG S , LAZICKI A , MILITZER B , et al. Equation of state of boron nitride combining computation, modeling, and experiment[J]. Phys Rev B, 2019, 99, 165103. DOI
66	ZHANG S , DRIVER K P , SOUBIRAN F , et al. First principles equation of state and shock compression predictions of warm dense hydrocarbons[J]. Phys Rev E, 2017, 96, 013204. DOI
67	ZHANG S , MILITZER B , BENEDICT L X , et al. Path integral Monte Carlo simulations of dense carbon-hydrogen plasmas[J]. J Chem Phys, 2018, 148, 102318. DOI
68	SOUBIRAN F , GONZÁLEZ-CATALDO F , DRIVER K P , et al. Magnesium oxide at extreme temperatures and pressures studied with first-principles simulations[J]. J Chem Phys, 2019, 151, 214104. DOI
69	GONZÁLEZ-CATALDO F , SOUBIRAN F , PETERSON H , et al. Path integral Monte Carlo and density functional molecular dynamics simulations of warm dense MgSiO₃[J]. Phys Rev B, 2020, 101, 024107. DOI
70	CEPERLEY D M . Fermion nodes[J]. J Stat Phys, 1991, 63, 1237- 1267. DOI
71	MILITZER B , POLLOCK E L . Variational density matrix method for warm, condensed matter: Application to dense hydrogen[J]. Phys Rev E, 2000, 61, 3470- 3482.
72	POLLOCK E L . Properties and computation of the Coulomb pair density matrix[J]. Comput Phys Commun, 1988, 52, 49- 60. DOI
73	SCHOOF T , BONITZ M , FILINOV A , et al. Configuration path-integral Monte Carlo[J]. Contrib Plasma Phys, 2011, 51, 687- 697. DOI
74	SCHOOF T , GROTH S , BONITZ M . Towards ab initio thermodynamics of the electron gas at strong degeneracy[J]. Contrib Plasma Phys, 2015, 55, 136- 143. DOI
75	ZAN Xiaolei. Path integral Monte Carlo simulations of the warm dense electron systems[D]. Changsha: National University of Defense Technology, 2017.
76	SCHOOF T , GROTH S , VORBERGER J , et al. Ab initio thermodynamics results for the degenerate electron gas at finite temperature[J]. Phys Rev Lett, 2015, 115, 130402. DOI
77	DORNHEIM T , GROTH S , FILINOV A , et al. Permutation blocking path integral Monte Carlo: A highly efficient approach to the simulation of strongly degenerate non-ideal fermions[J]. New J Phys, 2015, 17, 073017. DOI
78	BONINSEGNI M , PROKOF'EV N , SVISTUNOV B . Worm algorithm for continuous-space path integral Monte Carlo simulations[J]. Phys Rev Lett, 2006, 96, 070601. DOI
79	BONINSEGNI M , PROKOF'EV N , SVISTUNOV B . Worm algorithm and diagrammatic Monte Carlo: A new approach to continuous-space path integral Monte Carlo simulations[J]. Phys Rev E, 2006, 74, 036701. DOI
80	DORNHEIM T , SCHOOF T , GROTH S , et al. Permutation blocking path integral Monte Carlo approach to the uniform electron gas at finite temperature[J]. J Chem Phys, 2015, 143, 204101. DOI
81	PERDEW J P , ZUNGER A . Self-interaction correction to density-functional approximations for many-electron systems[J]. Phys Rev B, 1981, 23, 5048- 5079. DOI
82	FILINOV V S , FORTOV V E , BONITZ M , et al. Fermionic path-integral Monte Carlo results for the uniform electron gas at finite temperature[J]. Phys Rev E, 2015, 91, 033108. DOI
83	BROWN E W , CLARK B K , DUBOIS J L , et al. Path-integral Monte Carlo simulation of the warm dense homogeneous electron gas[J]. Phys Rev Lett., 2013, 110, 146405. DOI
84	MCMAHON J M , MORALES M A , PIERLEONI C , et al. The properties of hydrogen and helium under extreme conditions[J]. Rev Mod Phys, 2012, 84, 1607- 1653. DOI
85	LV Wenjuan , WU Binbing , LIU Shiwei , et al. Progress in the study of deteron-triton fusion cross sections in superintense laser fields[J]. Chinese Journal of Computational Physics, 2022, 39 (2): 127- 142.
86	FILINOV V S , LEVASHOV P R , BONITZ M , et al. Calculation of the shock hugoniot of deuterium at pressures above 1 Mbar by the path-integral Monte Carlo method[J]. Plasma Phys Rep, 2005, 31, 760- 764.
87	MILITZER B , GONZÁLEZ-CATALDO F , ZHANG S , et al. First-principles equation of state database for warm dense matter computation[J]. Phys Rev E, 2021, 103, 013203. DOI
88	HU S X , COLLINS L A , GONCHAROV V N , et al. First-principles equation of state of polystyrene and its effect on inertial confinement fusion implosions[J]. Phys Rev E, 2015, 92, 043104. DOI
89	MILITZER B , GONZÁLEZ-CATALDO F , ZHANG S , et al. Nonideal mixing effects in warm dense matter studied with first-principles computer simulations[J]. J Chem Phys, 2020, 153, 184101. DOI
90	CHIN S A . High-order path-integral Monte Carlo methods for solving quantum dot problems[J]. Phys Rev E, 2015, 91, 031301(R). DOI
91	ZHANG Linfeng , HAN Jiequn , WANG Han , et al. Deep potential molecular dynamics: A scalable model with the accuracy of quantum mechanics[J]. Phys Rev Lett, 2018, 120, 143001. DOI

[1]	Zongduo WU, Qingyang MAN, Jin YAN, Jianhua PANG, Yifang SUN. Applications of Three-component Mie-GrüNeisen Mixture Model in Underwater Explosion Mitigation Problem [J]. Chinese Journal of Computational Physics, 2023, 40(5): 556-569.
[2]	NIU Xiao, NI Guoxi, MA Wenhua. Application of Adaptive Multi-resolution Method in Numerical Simulation of Reactive Multiphase Flows [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(6): 639-652.
[3]	ZHANG Qili, LIU Haifeng, LI Qiong, SONG Hongzhou, ZHANG Gongmu. Path Integral Monte Carlo Calculations of Equation of State of Hydrogen [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2019, 36(4): 379-385.
[4]	LIU Jingjing, ZENG Xianyang, NI Guoxi. Euler Numerical Methods for Reactive Flow with General Equation of States in Two Dimensions [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(1): 29-38.
[5]	ZHAO Yanhong, ZHANG Gongmu, ZHANG Qili, LI Qiong. Equation of State of Detonation Products for HMX Explosive [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2017, 34(2): 155-159.
[6]	XU Liang, FENG Chengliang, LIU Tiegang. Design Principles of Ghost Fluid Method [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2016, 33(6): 671-680.
[7]	TANG Weijun, JIANG Lang, CHENG Junbo. Algorithm Preserving Mass Fraction Maximum Principle for Multi-component Flows [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2014, 31(3): 292-306.
[8]	HUANG Xia, TANG Wenhui, JIANG Banghai, WANG Daorong. A Modified PUFF Equation of State for Anisotropic Materials [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2011, 28(3): 368-374.
[9]	LIANG Xianhong, LI Zheng, HE Changjiang, LIU Chao. Closing Relations in Two-step Eulerian Method for Multifluid Dynamics [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2010, 27(5): 658-664.
[10]	ZHENG Jianguo, MA Dongjun, SUN Dejun, YIN Xieyuan. Piecewise Parabolic Method for Compressible Multi-fluid Flows with van der Waals Equation of State [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2007, 24(3): 287-294.
[11]	MA Dong-jun, SUN De-jun, YIN Xie-yuan. Numerical Methods for One-dimensional Compressible Multi-fluid Flow [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2003, 20(2): 183-188.
[12]	Sun Fengguo, Hu Hongbo, Tang Rongqi. NUMERICAL CALCULATION OF EOS AND PHASE DIAGRAM FOR TWO DIMENSIONAL HARD DISK SYSTEM [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 1992, 9(1): 35-39.
[13]	Wang Yiren, Li Hong, Yao Jin, Wang Weizhong. THE EQUATION OF STATE AND SN EXPLOSION [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 1990, 7(3): 321-331.