Dynamics and Implementation of Memristive System Exhibiting Extreme Multistability

doi:10.19596/j.cnki.1001-246x.8760

Abstract

Abstract:

Based on a class of parameter-adjustable chaotic systems, an improved four-dimensional memristive chaotic system is established by replacing the gain resistor of the original system circuit with a memristor. Theoretical analysis demonstrates that the new system possesses two line equilibrium points and can generate self-excited attractors. The dynamics of the new system are analyzed through numerical simulation such as bifurcation diagrams, Lyapunov exponents, phase diagrams, etc. With the variation of initial conditions, the memristive system with fixed parameters exhibits not only the extreme multistability phenomenon of coexisting infinitely many attractors but also complex transient behaviors. Finally, to validate the theoretical and numerical simulation results, an equivalent circuit of the memristive chaotic system is designed, and hardware circuit experiments as well as PSIM circuit simulations confirm the correctness of the MATLAB numerical simulations.

Key words: flux-controlled memristor, line equilibrium, extreme multistability, transient behavior

CLC Number:

TN711.4

Ji CHEN, Yi XU, Jinfu LIU, Tao LIU. Dynamics and Implementation of Memristive System Exhibiting Extreme Multistability[J]. Chinese Journal of Computational Physics, 2024, 41(4): 523-534.

Figures/Tables 17

Fig.1 Circuit construction of memristor chaotic system

Fig.2 Equivalent circuit of system (1) and realization circuit of memristor chaotic system

Fig.3 Equivalent circuit of memristor

Fig.4 Phase portrait of typical attractor (a) x-z plane; (b) w-y plane

Fig.5 Dynamics of system (5) with respect to z(0) (a) bifurcation diagram; (b) Lyapunov exponents spectra

Fig.6 Dynamics of system (5) with respect to x(0) (a) bifurcation diagram; (b) Lyapunov exponents spectra

Fig.7 Dynamics of system (5) with respect to w(0) (a) bifurcation diagram; (b) Lyapunov exponents spectra

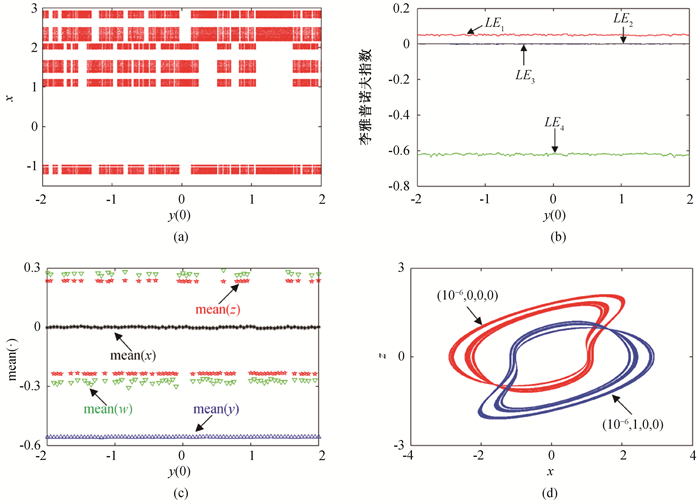
Fig.8 Dynamics of system (5) with respect to y(0) (a) bifurcation diagram; (b) Lyapunov exponents spectra; (c) mean values graph; (d)phase diagram of weak chaotic attractor

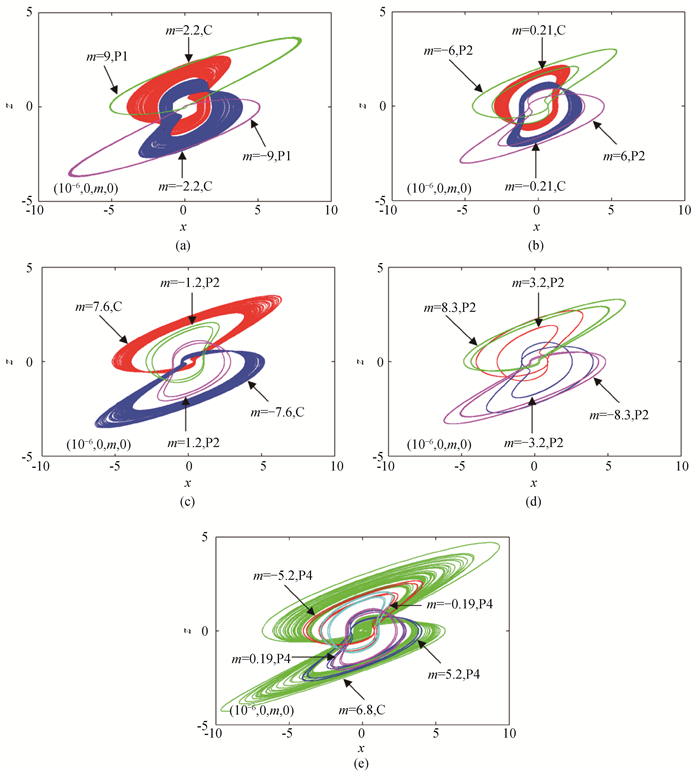
Fig.9 Phase portraits of the x-z plane with different initial conditions by MATLAB simulations (a) symmetrical single-wing chaotic attractor and symmetrical period-1 limitcycle; (b) symmetrical single-wing chaotic attractor and symmetrical period-2 limitcycle; (c) symmetrical single-wing chaotic attractor and symmetrical period-2 limitcycle; (d) four kinds of period-2 limitcycle; (e) two-wing chaotic attractor and four kinds of period-2 limitcycle

Table 1 Comparison of system (5) and some same type systems

系统	原系统编号	固定参数下共存吸引子数量
系统1^[31]	VB5	2
系统2^[32]	VB18	17
系统3^[33]	VB3	6
系统(5)	VB5	21

Fig.10 Time-domain waveform and phase portraits by MATLAB simulations with x(0) = 10-6, y(0) = w(0) = 0 at (a) z(0) = 0.28 and (b) z(0) = -0.29

Fig.11 Time-domain waveform and phase portraits by MATLAB simulations with x(0) = 10-6, y(0) = z(0) = 0, w(0) = -12.45

Table 2 Circuit parameter values of system(5)

参数	定义	数值	参数	定义	数值
R	电阻	36 kΩ	v_b	电压	1 V
C	电容	100 nF	R_w	电阻	36 kΩ
R_a	电阻	10 kΩ	R₁	电阻	3 kΩ
R_α	电阻	36 kΩ	R₂	电阻	10 kΩ
R_β	电阻	72 kΩ

Fig.12 Hardware circuit experiment (a) (vx-vz) plane phase portrait; (b) (vw-vy) plane phase portrait

Fig.13 Phase portraits in the (vx-vz) plane with different initial conditions by PSIM simulations (a)symmetrical single-wing chaotic attractor and symmetrical period-1 limitcycle; (b)symmetrical single-wing chaotic attractor and symmetrical period-2 limitcycle; (c)symmetrical single-wing chaotic attractor and symmetrical period-2 limitcycle; (d)four kinds of period-2 limitcycle; (e)two-wing chaotic attractor and four kinds of period-2 limitcycle

Fig.14 Time-domain waveform and phase portraits by PSIM simulations with vx(0) = 10-6 V, vy(0) = vw(0) = 0 V (a) vz(0) = 0.28 V; (b) vz (0) = -0.29 V

Fig.15 Time-domain waveform and phase portraits by PSIM simulations with vx(0) = 10-6 V, vy (0) = vz(0) = 0 V, vw(0) = -12.45 V

References 34

1	陈墨, 陈成杰, 包伯成, 等. 忆阻突触耦合Hopfield神经网络的初值敏感动力学[J]. 电子与信息学报, 2020, 42 (4): 870- 877.
2	MARCO D M , FORTI M , PANCIONI L , et al. Memristor neural networks for linear and quadratic programming problems[J]. IEEE Transactions on Cybernetics, 2022, 52 (3): 1822- 1835. DOI
3	王春华, 蔺海荣, 孙晶如, 等. 基于忆阻器的混沌、存储器及神经网络电路研究进展[J]. 电子与信息学报, 2020, 42 (4): 795- 810.
4	唐利红, 贺宗梅, 姚延立. 忆阻Hopfield神经网络动力学分析及其电路实现[J]. 计算物理, 2022, 39 (2): 244- 252.
5	周倩, 韦笃取. 场耦合忆阻神经网络的电活动[J]. 计算物理, 2020, 37 (6): 750- 756.
6	闵富红, 王珠林, 王恩荣, 等. 新型忆阻器混沌电路及其在图像加密中的应用[J]. 电子与信息学报, 2016, 38 (10): 2681- 2688.
7	WANG Leimin , DONG Tiandu , GE Mingfeng . Finite-time synchronization of memristor chaotic systems and its application in image encryption[J]. Applied Mathematics and Computation, 2019, 347, 293- 305. DOI
8	孙亮, 罗佳, 乔印虎. 忆阻Hopfield神经网络的初值位移调控动力学及其图像加密应用[J]. 计算物理, 2023, 40 (1): 106- 116.
9	GU Shuangquan , PENG Qiqi , LENG Xiangxin , et al. A novel non-equilibrium memristor-based system with multi-wing attractors and multiple transient transitions[J]. Chaos, 2021, 31 (3): 033105. DOI
10	BAO Bocheng , JIANG Tao , WANG Guangyi , et al. Two-memristor-based Chua's hyperchaotic circuit with plane equilibrium and its extreme multistability[J]. Nonlinear Dynamics, 2017, 89 (2): 1157- 1171. DOI
11	YUAN Fang , WANG Guangyi , WANG Xiaowei . Extreme multistability in a memristor-based multi-scroll hyper-chaotic system[J]. Chaos, 2016, 26 (7): 073107. DOI
12	刘娣, 杨芳艳, 周国鹏, 等. 一类四维忆阻混沌电路的动力学行为分析[J]. 计算物理, 2018, 35 (4): 458- 468.
13	BAO Bocheng , BAO Han , WANG Ning , et al. Hidden extreme multistability in memristive hyperchaotic system[J]. Chaos Solitons & Fractals, 2017, 94, 102- 111.
14	BAO Bocheng , MA Zhenghua , XU Jianping , et al. A simple memristor chaotic circuit with complex dynamics[J]. International Journal of Bifurcation and Chaos, 2011, 21 (9): 2629- 2645. DOI
15	WANG Chunhua , LIU Xiaoming , HU Xia . Multi-piecewise quadratic nonlinearity memristor and its 2N-scroll and 2N + 1-scroll chaotic attractors system[J]. Chaos, 2017, 27 (3): 033114. DOI
16	WU Huagan , YE Yi , CHEN Mo , et al. Periodically switched memristor initial boosting behaviors in memristive hypogenetic jerk system[J]. IEEE Access, 2019, 7, 145022- 145029. DOI
17	NGONGHALA C N , FEUDEL U , SHOWALTER K . Extreme multistability in a chemical model system[J]. Physical Review E Statistical Nonlinear and soft Matter Physics, 2011, 83 (5 Pt 2): 056206.
18	PATEL M S , PATEL U , SEN A , et al. Experimental observation of extreme multistability in an electronic system of two coupled Rössler oscillators[J]. Physical Review E Statistical Nonlinear and soft Matter Physics, 2014, 89 (2): 022918. DOI
19	HENS C , DANA S K , FEUDEL U . Extreme multistability: Attractor manipulation and robustness[J]. Chaos, 2015, 25 (5): 053112. DOI
20	闵富红, 金秋森. 双忆阻Shinriki振荡器的超级多稳态和反单调性分析[J]. 电子学报, 2019, 47 (11): 2263- 2270.
21	BAO Han , WANG Ning , BAO Bocheng , et al. Initial condition-dependent dynamics and transient period in memristor-based hypogenetic jerk system with four line equilibria[J]. Communications in Nonlinear Science and Numerical Simulation, 2018, 57, 264- 275. DOI
22	BAO Han , CHEN Mo , WU Huagan , et al. Memristor initial-boosted coexisting plane bifurcations and its extreme multi-stability reconstitution in two-memristor-based dynamical system[J]. Science China Technological Sciences, 2020, 63 (4): 603- 613.
23	李志军, 曾以成. 基于文氏振荡器的忆阻混沌电路[J]. 电子与信息学报, 2014, 36 (1): 88- 93.
24	BAO Han , LIU Wenbo , CHEN Mo . Hidden extreme multistability and dimensionality reduction analysis for an improved non-autonomous memristive FitzHugh-Nagumo circuit[J]. Nonlinear Dynamics, 2019, 96 (3): 1879- 1894.
25	ZHANG Jihong , LIAO Xiaofeng . Effects of initial conditions on the synchronization of the coupled memristor neural circuits[J]. Nonlinear Dynamics, 2019, 95 (2): 1269- 1282.
26	CHEN Mo , BAO Bocheng , JIANG Tao , et al. Flux-charge analysis of initial state-dependent dynamical behaviors of a memristor emulator-based Chua's circuit[J]. International Journal of Bifurcation and Chaos, 2018, 28 (10): 1850120.
27	FITCH A L , YU Dongsheng , IU H H C , et al. Hyperchaos in a memristor-based modified canonical Chua's circuit[J]. International Journal of Bifurcation and Chaos, 2012, 22 (6): 1250133.
28	MA Jun , WU Fuqiang , REN Guodong , et al. A class of initials-dependent dynamical systems[J]. Applied Mathematics and Computation, 2017, 298, 65- 76.
29	LI Chunbiao , SPROTT J C . Variable-boostable chaotic flows[J]. Optik, 2016, 127 (22): 10389- 10398.
30	BAO Bocheng , QIAN Hui , XU Quan , et al. Coexisting behaviors of asymmetric attractors in hyperbolic-type memristor based hopfield neural network[J]. Frontiers in Computational Neuroscience, 2017, 11, 81.
31	ZHANG Xin , LI Chunbiao , CHEN Yudi , et al. A memristive chaotic oscillator with controllable amplitude and frequency[J]. Chaos Solitons & Fractals, 2020, 139, 110000.
32	HUANG Lili , WANG Yanling , JIANG Yicheng , et al. A novel memristor chaotic system with a hidden attractor and multistability and its implementation in a circuit[J]. Mathematical Problems in Engineering, 2021, 2021, 7457220.
33	秦铭宏, 赖强, 吴永红. 具有无穷共存吸引子的简单忆阻混沌系统的分析与实现[J]. 物理学报, 2022, 71 (16): 86- 96.
34	DADRAS S , MOMENI H R , QI Guoyuan . Analysis of a new 3D smooth autonomous system with different wing chaotic attractors and transient chaos[J]. Nonlinear Dynamics, 2010, 62 (1): 391- 405.

[1]	Lihong TANG, Zongmei HE, Yanli YAO. Magnetic Induction HR Neuron with Hidden Extreme Multistability and Its Circuit Implementation [J]. Chinese Journal of Computational Physics, 2022, 39(5): 589-597.
[2]	FANG Sidong, WANG Weihong, WU Yonghui, CHENG Linsong. Transient Behavior Analysis of Fractured Horizontal Wells Based on an Improved Green Element Method [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(1): 69-78.