用运动控制器来终止心律失常

doi:10.19596/j.cnki.1001-246x.8243

摘要/Abstract

摘要：

采用Luo-Rudy相Ⅰ心脏模型对通过局部电击使细胞复极化来消除心脏中的螺旋波和时空混沌进行数值模拟。提出利用控制器局部电击螺旋波波头周围的心肌细胞来抑制螺旋波的旋转，使螺旋波漂移出边界，进而控制螺旋波和时空混沌。数值模拟表明：适当选择控制的格点数和膜电位控制阈值，螺旋波和时空混沌都可以被抑制。最少的控制格点数为9个，最短的单螺旋波控制时间小于150 ms，最短的时空混沌控制时间小于500 ms。

关键词: 心律失常, 螺旋波, 时空混沌, 膜电位控制阈值

Abstract:

A control method suppressing spiral wave and spatiotemporal chaos by using local electric shock produced by moving controller is proposed. The local electric shock is to myocardial cells around spiral wave tip to suppress the rotation of spiral wave tip, causing spiral wave tip to move out of the boundary. We studied numerically with Luo-Rudy phase I heart model. It shows that with appropriate number of grid points controlled by local electrical shock and the control thresholds of membrane potential, both spiral wave and spatiotemporal chaos can be suppressed. The minimum number of controlled grid points is 9. The shortest control times of spiral wave and spatiotemporal chaos are less than 150 ms and 500 ms, respectively.

Key words: arrhythmia, spiral wave, spatiotemporal chaos, control threshold of membrane potential

中图分类号:

O415.5

白婧, 黄志精, 唐国宁. 用运动控制器来终止心律失常[J]. 计算物理, 2021, 38(3): 352-360.

Jing BAI, Zhijing HUANG, Guoning TANG. Terminating Arrhythmia by Using Motion Controller[J]. Chinese Journal of Computational Physics, 2021, 38(3): 352-360.

图/表 9

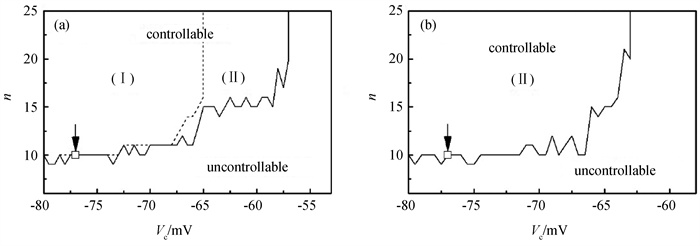
图1 在n-Vc参数平面上(a)螺旋波和(b)时空混沌的可控制区(□这个可控点及上方各点没有数值模拟确认。实线及上方为可控区，下方为不可控区。在虚线上方控制(Ⅰ)区螺旋波被快速控制。在可控制区(Ⅱ)螺旋波不能被快速控制。)

Fig.1 Controllable regions of (a) spiral wave and (b) spatiotemporal chaos in the n-Vc parameter plane (□ and the points above □ are controllable points that have not been confirmed by numerical simulation. The area above the solid curve is controllable area and the rest is uncontrollable area. The area above the dotted line in (a) is controllable area (Ⅰ) in which spiral wave can be controlled quickly. The other is controllable area (Ⅱ) in which spiral wave cannot be controlled quickly.)

图2 在n-Vc参数平面上(a)螺旋波和(b)时空混沌的控制时间分布

Fig.2 Control time distribution of (a) spiral wave and (b) spatiotemporal chaos in the n-Vc plane

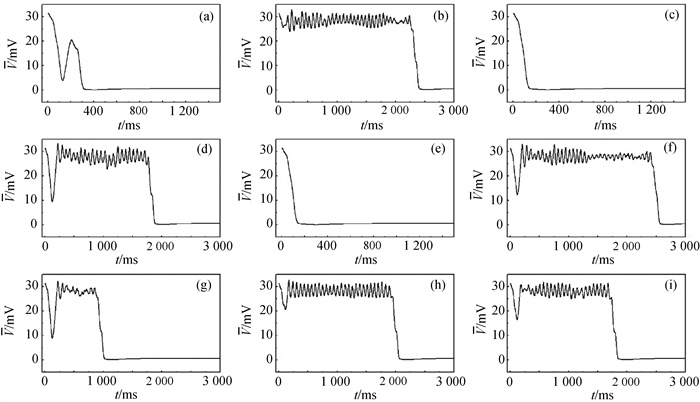
图3 ${\bar G}$si= 0.02 mS ·cm-2时平均膜电位差随时间的变化 (a) Vc=-78 mV，n= 9；(b)Vc=-73.5 mV，n= 9；(c) Vc=-73.5 mV，n= 10；(d) Vc= -65 mV，n= 15；(e) Vc= -65 mV，n= 16；(f) Vc= -62.5 mV，n= 16；(g) Vc= -62.5 mV，n= 25；(h) Vc= -59 mV，n= 16；(i) Vc= -59 mV，n= 25

Fig.3 Evolution of the mean membrane potential difference at ${\bar G}$si= 0.02 mS ·cm-2 (a) Vc=-78 mV, n= 9; (b) Vc=-73.5 mV, n= 9; (c) Vc=-73.5 mV, n= 10; (d) Vc= -65 mV, n= 15; (e) Vc= -65 mV, n= 16; (f) Vc= -62.5 mV, n= 16; (g) Vc= -62.5 mV, n= 25; (h)Vc= -59 mV, n= 16; (i) Vc= -59 mV, n= 25

图4 在${\bar G}$si= 0.02 mS ·cm-2，Vc = -73 mV和n = 10的情况下不同时刻的膜电位斑图 (a) t = 4 ms；(b) t = 20 ms；(c) t = 48 ms；(d) t = 104 ms

Fig.4 Patterns of membrane potential at different moments for ${\bar G}$si= 0.02 mS ·cm-2, Vc = -73 mV and n = 10 (a) t = 4 ms; (b) t = 20 ms; (c) t = 48 ms; (d) t = 104 ms

图5 图 4中各斑图的局部放大

Fig.5 Local blowup of patterns shown in Fig. 4

图6 在${\bar G}$si= 0.02 mS ·cm-2，Vc= -60 mV和n= 16情况不同时刻的膜电位斑图 (a) t= 4 ms；(b) t= 40 ms；(c) t= 248 ms；(d) t= 456 ms；(e) t= 712 ms；(f) t= 1 180 ms；(g) t= 1 560 ms；(h) t= 1 660 ms；(i) t= 1 760 ms

Fig.6 Patterns of membrane potential at different moments for ${\bar G}$si= 0.02 mS ·cm-2, Vc= -60 mV and n= 16 (a) t= 4 ms; (b) t= 40 ms; (c) t= 248 ms; (d) t= 456 ms; (e) t= 712 ms; (f) t= 1 180 ms; (g) t= 1 560 ms; (h) t= 1 660 ms; (i)t= 1 760 ms

图7 在${\bar G}$si= 0.02 mS ·cm-2螺旋波波头轨迹(a) Vc= -60 mV，n = 16；(b) Vc = -73 mV，n = 10

Fig.7 Trajectories of spiral wave tip at G si= 0.02 mS ·cm-2 (a) Vc= -60 mV, n = 16; (b) Vc= -73 mV, n = 10

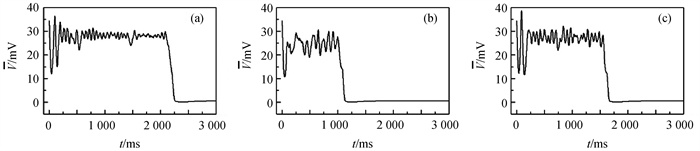
图8 在${\bar G}$si= 0.05 mS ·cm-2平均膜电位差随时间的变化(a) Vc= -72.5 mV，n = 10；(b) Vc= -72.5 mV，n = 20；(c) Vc= -63 mV，n = 20

Fig.8 Evolution of the mean membrane potential difference at ${\bar G}$si= 0.05 mS ·cm-2 (a) Vc= -72.5 mV, n = 10; (b) Vc= -72.5 mV, n = 20; (c) Vc= -63 mV, n = 20

图9 在${\bar G}$si= 0.05 mS ·cm-2，Vc= -66.5 mV和n = 12情况下不同时刻的膜电位斑图(a) t = 0 ms；(b) t = 20 ms；(c) t = 40 ms；(d) t = 140 ms；(e) t = 440 ms；(f) t = 800 ms；(g) t = 1 340 ms；(h) t = 1 580 ms；(i) t = 1 700 ms

Fig.9 Patterns of membrane potential at different moments for ${\bar G}$si= 0.05 mS ·cm-2, Vc= -66.5 mV and n = 12 (a) t = 0 ms; (b) t = 20 ms; (c) t = 40 ms; (d) t = 140 ms; (e) t = 440 ms; (f) t = 800 ms; (g) t = 1 340 ms; (h) t = 1 580 ms; (i) t = 1 700 ms

参考文献 34

1	DAVIDENKO J M, PERTSOV A V, SALOMONSZ R, et al. Stationary and drifting spiral waves of excitation in isolated cardiac muscle[J]. Nature, 1992, 355 (6358): 349- 351. DOI
2	DAVIDENKO J M, KENT P F, et al. Sustained vortex-like waves in normal isolated ventricular muscle[J]. Proceedings of the National Academy of Sciences, 1990, 87 (22): 8785- 8789. DOI
3	WITKOWSKI F X, LEON L J, PENKOSKE P A, et al. Spatiotemporal evolution of ventricular fibrillation[J]. Nature, 1998, 392 (6671): 78- 82. DOI
4	STEWART J A. Automated external defibrillators in the hospital: A case of medical reversal[J]. American Journal of Emergency Medicine, 2018, 36 (5): 871- 874. DOI
5	WALCOTT G P, KILLINGSWORTH C R, IDEKER R E. Do clinically relevant transthoracic defibrillation energies cause myocardial damage and dysfunction?[J]. Resuscitation, 2003, 59 (1): 59- 70. DOI
6	SANTANGELI P, MUSER D, MAEDA S, et al. Comparative effectiveness of antiarrhythmic drugs and catheter ablation for the prevention of recurrent ventricular tachycardia in patients with implantable cardioverter defibrillators: A systematic review and meta-analysis of randomized controlled trials[J]. Heart Rhythm, 2016, 13 (7): 1552- 1559. DOI
7	QIN D, LEEF G, ALAM M B, et al. Comparative effectiveness of antiarrhythmic drugs for rhythm control of atrial fibrillation[J]. Journal of Cardiology, 2016, 67 (5): 471- 476. DOI
8	BOKHARI F, NEWMAN D, GREENE M, et al. Long-term comparison of the implantable cardioverter defibrillator versus amiodarone eleven-year follow-up of a subset of patients in the Canadian implantable defibrillator study (CIDS)[J]. Circulation, 2004, 110 (2): 112- 116. DOI
9	HOLMQVIST F, KESEK M, ENGLUND A, et al. A decade of catheter ablation of cardiac arrhythmias in Sweden: Ablation practices and outcomes[J]. European Heart Journal, 2019, 40 (10): 820- 830. DOI
10	RAZMINIA M, WILLOUGHBY M C, DEMO H, et al. Fluoroless catheter ablation of cardiac arrhythmias: A 5-year experience[J]. Pacing and Clinical Electrophysiology, 2017, 40 (4): 425- 433. DOI
11	MARROUCHE N F, BRACHMANN J, ANDRESEN D, et al. Catheter ablation for atrial fibrillation with heart failure[J]. New England Journal of Medicine, 2018, 378 (5): 417- 427. DOI
12	NARAYAN S M, KRUMMEN D E, SHIVKUMAR K, et al. Treatment of atrial fibrillation by the ablation of localized sources[J]. Journal American College of Cardiology, 2012, 60 (7): 628- 636. DOI
13	NARAYAN S M, KRUMMEN D E, RAPPEL W J, et al. Clinical mapping approach to diagnose electrical rotors and focal impulse sources for human atrial fibrillation[J]. Journal of Cardiovascular Electrophysiology, 2012, 23 (5): 447- 454. DOI
14	CHENG E P, LIU C F, YEO I, et al. Risk of mortality following catheter ablation of atrial fibrillation[J]. Journal of the American College of Cardiology, 2019, 74 (18): 2254- 2264. DOI
15	BOHNEN M, STEVENSON W G, TEDROW U B, et al. Incidence and predictors of major complications from contemporary catheter ablation to treat cardiac arrhythmias[J]. Heart Rhythm, 2011, 8 (11): 1661- 1666. DOI
16	BINGEN B O, ENGELS M C, SCHALIJ M J, et al. Light-induced termination of spiral wave arrhythmias by optogenetic engineering of atrial cardiomyocytes[J]. Cardiovascular Research, 2014, 104 (1): 194- 205. DOI
17	MAJUMDER R, FEOLA I, TEPLENIN A S, et al. Optogenetics enables real-time spatiotemporal control over spiral wave dynamics in an excitable cardiac system[J]. eLife, 2018, 7, e41076. DOI
18	ZHANG H, CAO Z J, HU G, et al. Suppress winfree turbulence by local forcing excitable systems[J]. Physical Review Letters, 2005, 94 (18): 188301. DOI
19	ZHANG H, HU B, HU G. Suppression of spiral waves and spatiotemporal chaos by generating target waves in excitable media[J]. Physical Review E, 2003, 68 (2): 026134. DOI
20	YUAN G Y, YANG S P, et al. Elimination of spiral waves and spatiotemporal chaos by the pulse with a specific spatiotemporal configuration[J]. Chinese Physics B, 2008, 17 (5): 1925- 1934. DOI
21	王春妮, 马军. 分布式电流刺激抑制心肌组织中螺旋波[J]. 物理学报, 2013, 62 (8): 084501.
22	YANG C Y, LIU H Y, TANG G N. Simulation on control of spiral wave by two-stage pulse force[J]. Chinese Journal of Computational Physics, 2014, 31 (5): 625- 630.
23	潘军廷, 何银杰, 张宏, 等. 极化电场对可激发介质中螺旋波的控制[J]. 物理学报, 2020, 69 (8): 080503.
24	BOCCIA E, LUTHER S, PARLITZ U. Modelling far field pacing for terminating spiral waves pinned to ischaemic heterogeneities in cardiac tissue[J]. Philosophical Transactions of the Royal Society A, 2017, 375 (2096): 20160289. DOI
25	ZHONG M, TANG G N. Suppression of spiral waves and spatiotemporal chaos in cardiac tissues with controll of calcium and potassium ionic currents[J]. Chinese Journal of Computational Physics, 2011, 28 (1): 119- 124.
26	李倩昀, 黄志精, 唐国宁. 通过抑制波头旋转消除心脏中的螺旋波和时空混沌[J]. 物理学报, 2018, 67 (24): 248201. DOI
27	潘飞, 王小艳, 唐国宁, 等. 通过放慢钠通道开闭控制心脏中的螺旋波和时空混沌[J]. 物理学报, 2016, 65 (19): 198201. DOI
28	MA J, WU N J, et al. A local phase control of spiral and spatiotemporal chaos[J]. Chinese Journal of Computational Physics, 2006, 23 (2): 243- 248.
29	PANDIT S V, JALIFE J. Rotors and the dynamics of cardiac fibrillation[J]. Circulation Research, 2013, 112 (5): 849- 862. DOI
30	CHEN J X, WEI G N, LI B W, et al. Motion of spiral waves induced by local pacing[J]. Central European Journal of Physics, 2008, 6 (3): 427- 433.
31	LIU G Q, YING H P. Motion of spiral tip driven by local forcing in excitable media[J]. Chinese Physics B, 2014, 23 (5): 050502. DOI
32	LEE Y S, SONG J S, HWANG M, et al. A new efficient method for detecting phase singularity in cardiac fibrillation[J]. Plos One, 2016, 11 (12): e0167567. DOI
33	LUO C H, RUDY Y. A model of the ventricular cardiac action potential: Depolarization, repolarization, and their interaction[J]. Circulation Research, 1991, 68 (6): 1501- 1526. DOI
34	FAST V G, ROHR S, IDEKER R E. Nonlinear changes of transmembrane potential caused by defibrillation shocks in strands of cultured myocytes[J]. American Journal of Physiology-Heart and Circulatory Physiology, 2000, 278 (3): H688- H697. DOI

[1]	陈绍英, 王雪丽, 高志梅, 袁国勇. 环域反馈下复Ginzburg-Landau系统的螺旋波动力学行为[J]. 计算物理, 2022, 39(1): 118-126.
[2]	杜丹, 李帅, 阳璞琼, 冯军, 向东, 龚学余. 螺旋天线轴向长度对螺旋波传播、吸收的影响[J]. 计算物理, 2021, 38(6): 713-721.
[3]	关富荣, 李成乾, 邓敏艺. 激发介质相对不应态对螺旋波动力学行为的影响[J]. 计算物理, 2021, 38(6): 749-756.
[4]	黄志精, 白婧, 唐国宁. 单向耦合神经元网络中螺旋波的自发形成机制[J]. 计算物理, 2020, 37(5): 612-622.
[5]	张学良, 谭惠丽, 唐国宁, 邓敏艺. 心肌组织机械形变的元胞自动机模拟[J]. 计算物理, 2018, 35(3): 294-302.
[6]	杨翠云, 刘海英, 唐国宁. 两阶段脉冲控制螺旋波的数值模拟[J]. 计算物理, 2014, 31(5): 625-630.
[7]	陈茜琼, 邓敏艺, 唐国宁, 孔令江. 传导延迟对螺旋波动力学行为的影响[J]. 计算物理, 2013, 30(4): 620-626.
[8]	陈绍英, 袁国勇, 吴刚, 崔倩倩, 范红领. Lévy噪声与周期力共同驱动下的螺旋波动力学[J]. 计算物理, 2012, 29(4): 620-626.
[9]	黎广钊, 唐国宁. 激发介质中去极化对螺旋波动力学影响的数值研究[J]. 计算物理, 2011, 28(4): 626-632.
[10]	钟敏, 唐国宁. 通过控制钙和钾离子流抑制心脏中的螺旋波和时空混沌[J]. 计算物理, 2011, 28(1): 119-124.
[11]	马军, 吴宁杰, 应和平, 蒲忠胜. 局部相空间压缩实现对时空混沌和螺旋波的控制[J]. 计算物理, 2006, 23(2): 243-248.
[12]	岳丽娟, 沈柯. 耦合双稳映象格子模型的时空混沌控制[J]. 计算物理, 2005, 22(2): 130-136.
[13]	闫广武. 激励介质中非线性化学波的格子Boltzmann模型[J]. 计算物理, 2003, 20(4): 356-358.
[14]	张志东, 卢遵铭. 液晶胆甾相中的分子短程关联[J]. 计算物理, 2003, 20(3): 215-218.
[15]	王金兰, 陈光旨. 时空混沌系统的主动-间隙耦合同步[J]. 计算物理, 1999, 16(5): 511-516.