DLR-F11高升力构型的数值模拟

doi:10.19596/j.cnki.1001-246x.8612

摘要/Abstract

摘要：

基于国家数值风洞(NNW)风雷软件(PHengLEI), 针对AIAA第二届高升力会议DLR-F11全机构型开展气动特性数值模拟, 以评估软件对复杂高升力外形低速流动模拟能力。研究内容主要包括网格收敛性分析、雷诺数影响分析, 以及缝翼滑轨和襟翼滑轨整流罩影响分析。通过与试验结果、其他参考值对比分析表明: 对高升力外形, 软件在线性段的计算结果具有较高可信度, 在失速迎角附近的模拟结果也与参考值相当, 在考虑滑轨和滑轨整流罩等复杂构型后, 也能正确捕捉到关键分离流动特征。

关键词: 高升力构型, 计算流体力学, 风雷软件, 大迎角流动

Abstract:

In order to evaluate the simulation capability of the National Numerical Wind-tunnel CFD software PHengLEI for subsonic flows over the complex high lift configuration, the 2nd AIAA High-Lift Prediction Workshop DLR-F11 configuration is selected and simulated. The grid convergence analysis, the Reynolds number effects and the influence of the slat track as well as the flap track faring are presented. The comparison with the experimental data and reference values indicates that the results have good credibility and validity in the linear segment before stall, and the results near angle of stall agree well with reference values. With the additional components of the slat track and the flap track fairing, separated flow features on the wing can be correctly captured.

Key words: high lift configuration, computatinal fluid dynamics, NNW-PHengLEI, high alpha flows

郭勇颜, 曾志春, 何磊, 何乾伟, 严雪琴, 赵钟. DLR-F11高升力构型的数值模拟[J]. 计算物理, 2023, 40(4): 401-415.

Yongyan GUO, Zhichun ZENG, Lei HE, Qianwei HE, Xueqin YAN, Zhong ZHAO. Numerical Simulation of DLR-F11 High-lift Configuration[J]. Chinese Journal of Computational Physics, 2023, 40(4): 401-415.

图/表 21

表1 DLR-F11构型几何尺寸

Table 1 The geometry details of DLR-F11 model

Main dimensions	Half span/m	Wing Ref. area/m²	MAC/m	Aspect ratio	Taper ratio	0.25 Chord sweep/°	Fuselage length/m
Value	1.4	0.419 13	0.347 09	-9.353	0.3	30	3.077

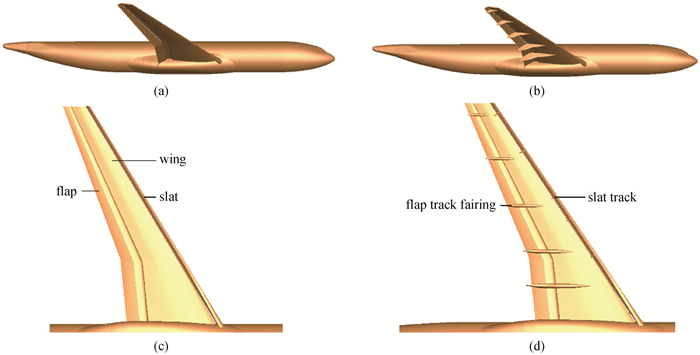
图1 DLR-F11几何构型(a) Case 1几何构型；(b)Case 2几何构型；(c) Case 1部件；(d) Case 2部件

Fig.1 The geometry of DLR-F11 model (a) configuration of Case 1; (b) configuration of Case 2; (c) component of Case 1; (d) component of Case 2

图2 Case 1的计算网格(a) 粗；(b) 中；(c) 细

Fig.2 Three types of computational grids of Case 1 (a) coarse; (b) medium; (c) fine

图3 Case 2的计算网格(a) 物面网格；(b) 缝翼滑轨；(c) 襟翼滑轨整流罩

Fig.3 Computational grids of Case 2 (a) surface grid; (b) slat track; (c) flap track faring

表2 DLR-F11计算网格信息

Table 2 Details of computational grids of DLR-F11

	grid name	单元数/10⁶	节点数/10⁶	第一层网格高度/(10^-7 m)
Case 1	coarse	15.15	5.99	7.0
	medium	24.87	8.71	6.1
	fine	38.65	12.36	5.3
Case 2	coarse	42.87	16.19	6.1
	medium	84.91	38.78	4.3
	fine	170.32	59.09	3.1

图4 Case 1网格收敛性分析(a) 升力系数；(b) 阻力系数

Fig.4 Grid convergence analysis for Case 1 (a) CL; (b) CD

图5 压力系数展向站位示意图

Fig.5 Sketch map of spanwise locations of pressure coefficient

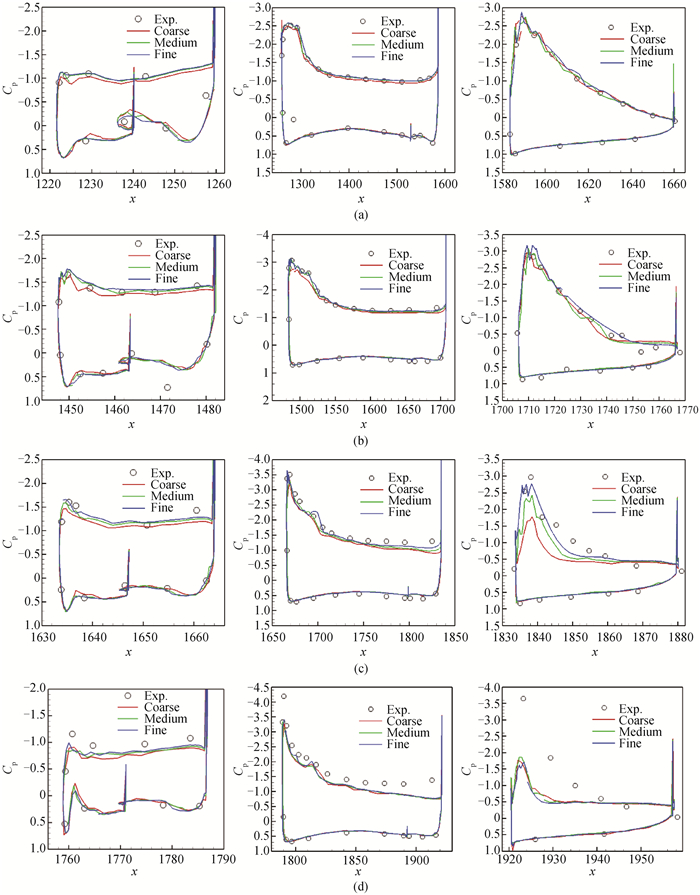
图6 Case 1中7°迎角下典型站位的物面压力系数分布(a) 28.8%站位；(b) 54.3%站位；(c) 75.1%站位；(d) 89.1%站位(左：缝翼; 中：主翼; 右：襟翼)

Fig.6 Pressure coefficient distribution at typical locations for Case 1 with α=7° (a)spanwise location =28.8%;(b) spanwise location =54.3%; (c) spanwise location =75.1%;(d)spanwise location =89.1% (left: slat; middle: wing; right: fllap)

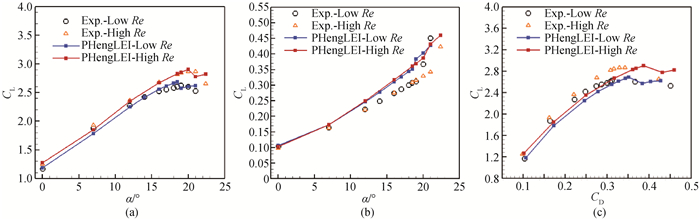
图7 Case 2Ⅱ高雷诺数下不同网格密度升力系数计算与试验结果

Fig.7 Lift coefficients between CFD and experiment for Case 2 Ⅱ under different grid densities

图8 Case 2气动力系数计算与试验结果(a) 升力系数随迎角变化；(b) 阻力系数随迎角变化；(c) 升力系数随阻力系数变化

Fig.8 Aerodynamic coefficient between CFD and experiment for Case 2 (a) CL vs α; (b) CD vs α; (c)CL vs CD

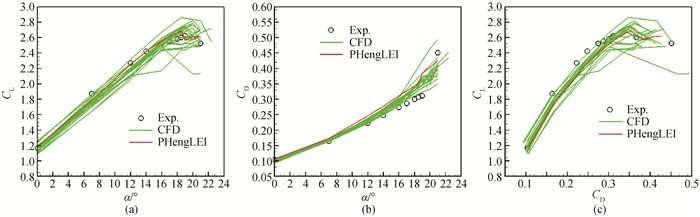
图9 低雷诺数Case 2Ⅰ气动力系数计算与参会结果(a) 升力系数随迎角变化；(b) 阻力系数随迎角变化；(c) 升力系数随阻力系数变化

Fig.9 Aerodynamic coefficient between PHengLEI and the other CFD softwares for Case 2Ⅰ(a) CL vs α; (b) CD vs α; (c)CL vs CD

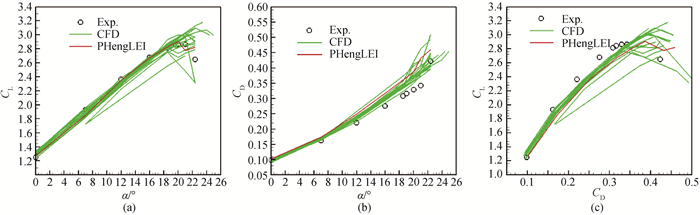
图10 高雷诺数Case 2Ⅱ气动力系数计算与参会结果(a) 升力系数随迎角变化；(b) 阻力系数随迎角变化；(c) 升力系数随阻力系数变化

Fig.10 Aerodynamic coefficient between PHengLEI and the other CFD softwares for Case 2Ⅱ(a) CL vs α; (b) CD vs α; (c)CL vs CD

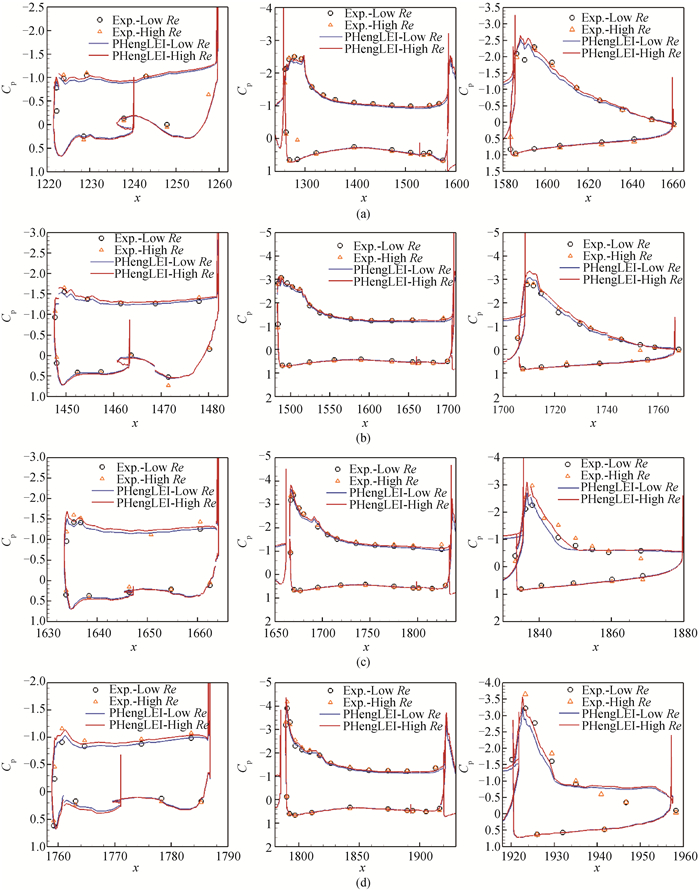
图11 Case 2，7°迎角下典型站位的物面压力系数分布(a)28.8%站位；(b) 54.3%站位；(c) 75.1%站位；(d) 89.1%站位(左：缝翼; 中：主翼; 右：襟翼)

Fig.11 Pressure coefficient distribution at typical locations for Case 2 with α=7° (a)spanwise location =28.8%;(b) spanwise location =54.3%; (c) spanwise location =75.1%; (d)spanwise location =89.1%(left: slat; middle: wing; right: fllap)

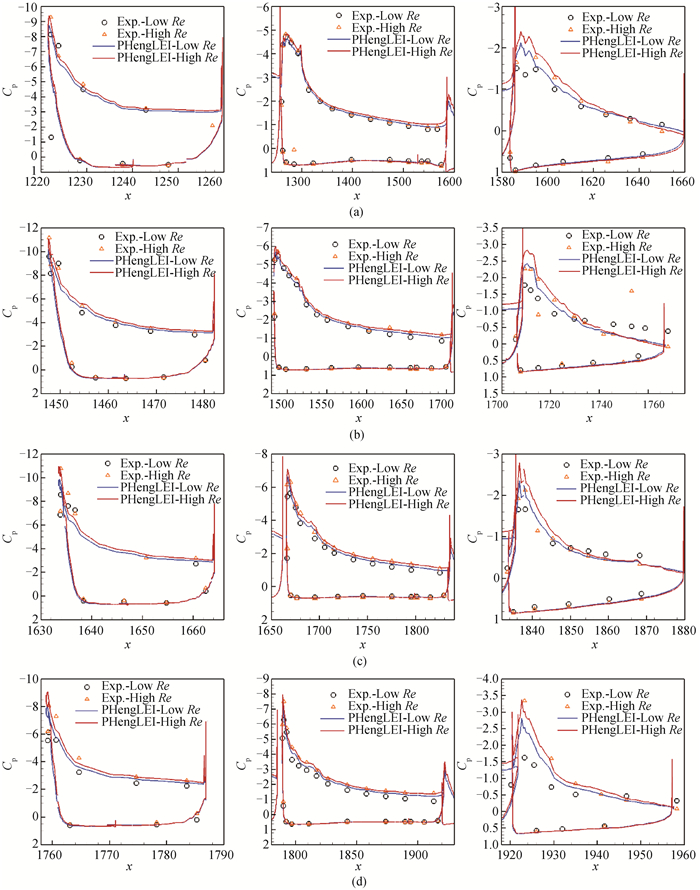
图12 Case 2, 18.5°迎角下典型站位的物面压力系数分布(a)28.8%站位；(b) 54.3%站位；(c) 75.1%站位；(d) 89.1%站位(左：缝翼; 中：主翼; 右：襟翼)

Fig.12 Pressure coefficient distribution at typical locations for Case 2 with α=18.5° (a) spanwise location =28.8%;(b) spanwise location =54.3%; (c) spanwise location =75.1%; (d) spanwise location =89.1%.(left: slat; middle: wing; right: fllap)

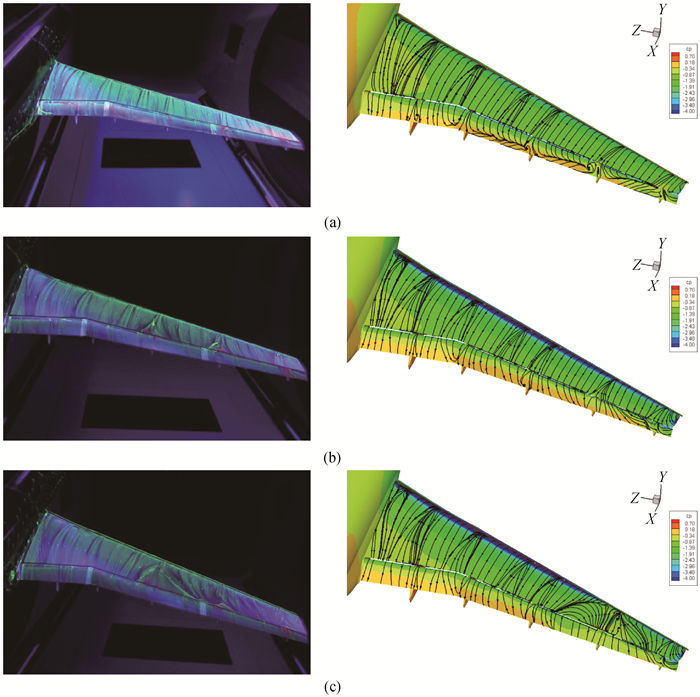
图13 Case 2Ⅰ壁面极限流线与试验油流图(a) 7°迎角；(b) 18.5°迎角；(c) 21°迎角

Fig.13 Surface streamlines between CFD and experiment for Case 2Ⅰ (a) α=7°; (b) α=18.5°; (c) α=21°

图14 Case 2Ⅱ空间流线(湍流粘性系数着色) (a) 16°迎角；(b) 18.5°迎角；(c) 21°迎角；(d) 22.4°迎角

Fig.14 Streamlines for space distribution for Case 2Ⅱ (colored by turbulent viscosity)(a) α=16°; (b) α=18.5°; (c) α=21°; (d) α=22.4°

图15 速度型位置示意图

Fig.15 Sketch map of locations of velocity profiles

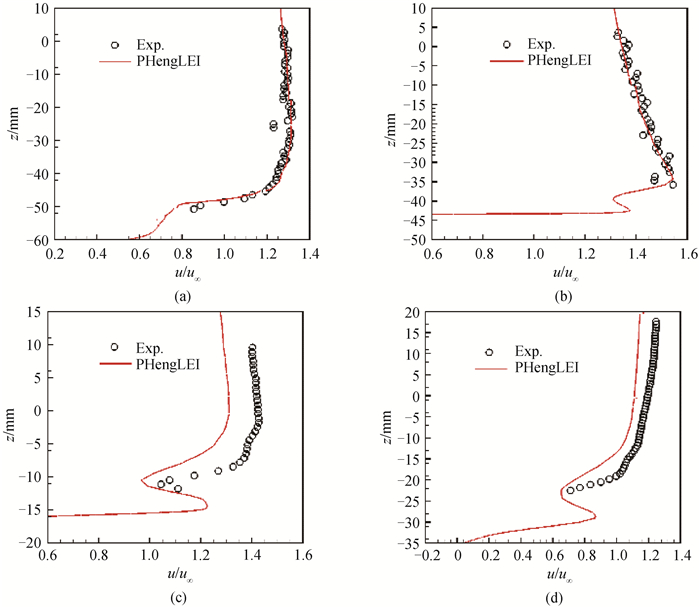
图16 Case 2Ⅰ, 7°迎角下典型位置速度型分布(a) R1B1；(b) R1B2；(c) R2E1；(d) R2E2

Fig.16 Velocity profiles at typical locations for Case 2 Ⅰ with α=7° (a) R1B1;(b) R1B2; (c) R2E1; (d) R2E2

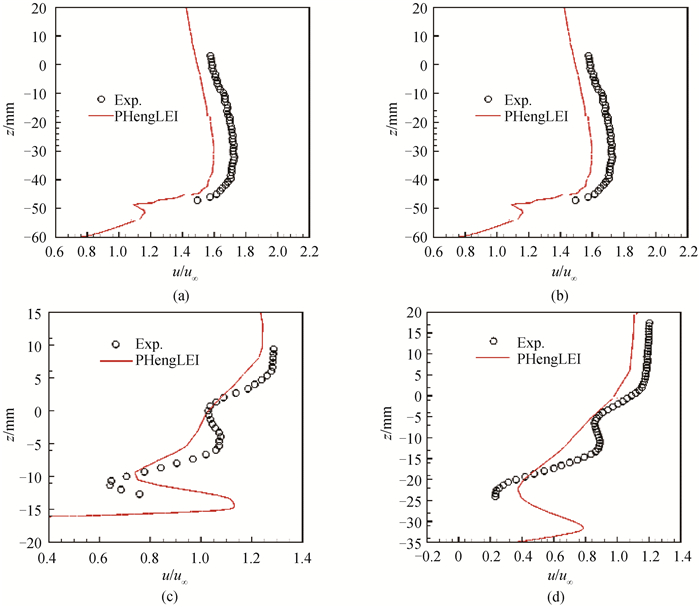
图17 Case 2Ⅰ, 18.5°迎角下典型位置速度型分布(a) R1B1；(b) R1B2；(c) R2E1；(d) R2E2

Fig.17 Velocity profiles at typical locations for Case 2Ⅰ with α=18.5° (a) R1B1; (b) R1B2; (c) R2E1; (d) R2E2

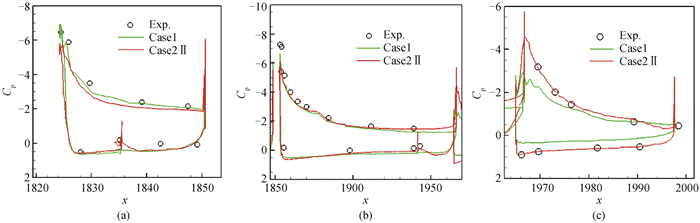
图18 21°迎角96%站位处压力分布(a) 缝翼；(b) 主翼；(c) 襟翼

Fig.18 Pressure coefficient distribution between Case 1 and Case 2Ⅱ at 96% span location with α=21° (a) slat; (b) wing; (c) flap

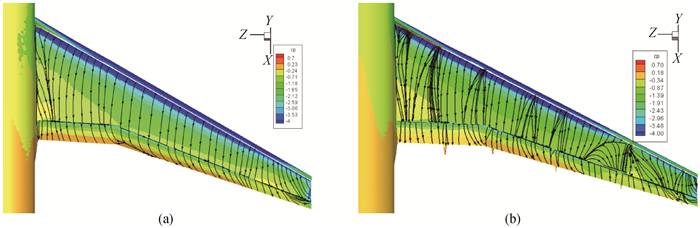
图19 21°迎角壁面极限流线(a) Case 1无滑轨；(b) Case 2Ⅱ有滑轨

Fig.19 Surface streamlines between Case 1 and Case 2Ⅱ with α=21° (a) Case 1: model with no slat track; (b) Case 2Ⅱ: model with the slat track

参考文献 26

1	邓小刚, 宗文刚, 张来平, 等. 计算流体力学中的验证和确认[J]. 力学进展, 2007, 37 (2): 279- 288.
2	朱自强, 陈迎春, 吴宗成, 等. 高升力系统外形的数值模拟计算[J]. 航空学报, 2005, 26 (3): 2576- 162.
3	RUMSEY C L, LONG M, STUEVER R A, et al. Summary of the first AIAA CFD high lift prediction workshop: AIAA-2011-939[R]. Reston, VA: AIAA, 2011.
4	RUMSEY C L , SLOTNICK J P . Overview and summary of the second AIAA high-lift prediction workshop[J]. Journal of Aircraft, 2015, 52 (4): 1006- 1025. DOI
5	RUMSEY C L , SLOTNICK J P , SCLAFANI A J . Overview and summary of the third AIAA high lift prediction workshop[J]. Journal of Aircraft, 2019, 56 (2): 621- 644. DOI
6	王运涛. HiLift-1~HiLiftPW-3数值模拟技术综述[J]. 航空学报, 2018, 39 (7): 021997.
7	HANKE J, SHANKARA H P, SNYDER D. Numerical simulation of DLR-F11 high lift configuration from HiLiftPW-2 using STAR-CCM+[C]//52nd Aerospace Sciences Meeting, 2014: 13-17.
8	ESCOBAR J A, SUARE C A, SILVA C, et al. Detached eddy simulation of the DLR-F11 wing/body configuration as a contribution to the 2nd AIAA CFD high lift prediction workshop[C]//32nd AIAA Applied Aerodynamics Conference, 2014: 16-20.
9	CHITALE K C , RASQUIN M , MARTIN J , et al. Finite element flow simulations of the EUROLIFT DLR-F11 high lift conguration[J]. Eprint Arxiv, 2014, 14- 18.
10	RASQUIN M, CHITALE K, ALI M, et al. Parallel adaptive detached eddy simulations of the EUROLIFT DLR-F11 high lift conguration[C]//32nd AIAA Applied Aerodynamics Conference, 2014: 16-20.
11	XUAN H , CHENG S , NING H , et al. The numerical simulation of civil transportation high-lift configuration[J]. Procedia Engineering, 2015, 99, 368- 376. DOI
12	赵钟, 赫新, 张来平, 等. HyperFLOW软件数值模拟TrapWing高升力外形[J]. 空气动力学学报, 2015, 33 (5): 594- 602.
13	赵钟, 何磊, 徐庆新, 等. 风雷软件数值模拟JSM高升力外形[C]//第十七届全国计算流体力学会议. 杭州, 2017: 108-112.
14	2nd AIAA CFD high lift prediction workshop[EB/OL]. (2021-01-09)[2022-03-01]. http://hiliftpw.larc.nasa.gov/index-workshop2.html.
15	陈坚强. 国家数值风洞(NNW)工程关键技术研究进展[J]. 中国科学: 技术科学, 2021, 51 (11): 1326- 1347.
16	赵钟, 张来平, 何磊, 等. 通用CFD软件风雷设计[J]. 计算机工程与科学, 2020, 42 (2): 210- 219.
17	陈坚强, 马燕凯, 闵耀兵, 等. 国家数值风洞(NNW)通用软件同构混合求解器设计[J]. 空气动力学学报, 2020, 38 (6): 1103- 1110.
18	赵钟, 张来平, 何磊, 等. 适用于任意网格的大规模并行CFD计算框架PHengLEI[J]. 计算机学报, 2019, 42 (11): 2368- 2383.
19	GAO L M , LI K T , LIU B , et al. General integral conservation from of Navier-Stokes equations and numerical application[J]. Chinese Journal of Computational Physics, 2008, 25 (2): 7.
20	HAN Z H , SONG W P , QIAO Z D . Numerical simulation of active stall control on high lift airfoil[J]. Chinese Journal of Computational Physics, 2009, 26 (6): 5.
21	SPALART P R, ALLMARAS S R A. One equation turbulence model for aerodynamic flows[C]//30th Aerospace Sciences Meeting & Exhibit, 1992: 1-22.
22	洪俊武, 王运涛, 李伟, 等. HiLiftPW-3高升力构型数值模拟[J]. 航空学报, 2019, 40 (3): 122391.
23	张彦军, 赵轲, 张同鑫, 等. 雷诺数变化对翼型边界层发展及失速特性的影响[J]. 航空工程进展, 2019, 10 (3): 319- 329.
24	DENG F , WU Y Z , LIU X Q . Simulation of vortex in separated flows with DES[J]. Chinese Journal of Computational Physics, 2008, 25 (6): 683- 688.
25	王运涛, 王光学, 张玉伦. 30P-30N多段翼型复杂流场数值模拟技术研究[J]. 空气动力学学报, 2010, 28 (1): 99- 103.
26	周云龙. WCNS-E-5在低速复杂流动中的应用研究[D]. 长沙: 国防科学技术大学, 2017.

[1]	孙天野, 祝宝山, 王红彪. 平面叶栅边界层的转捩试验及数值模拟[J]. 计算物理, 2023, 40(3): 307-313.
[2]	肖聪, 张士诚, 马新仿, 周彤, 侯腾飞. 基于模型降维和递归神经网络的油藏参数反演[J]. 计算物理, 2022, 39(5): 564-578.
[3]	张珑慧, 由长福. 基于有限体积虚拟区域方法的两相流动直接模拟[J]. 计算物理, 2019, 36(3): 291-297.
[4]	陈荣钱, 伍贻兆, 夏健. 应用随机模型方法预测汽车风噪声[J]. 计算物理, 2013, 30(1): 98-104.
[5]	邓枫, 覃宁, 伍贻兆. EGO方法的训练算法及应用[J]. 计算物理, 2012, 29(3): 326-332.
[6]	陈荣钱, 伍贻兆, 夏健. 基于SNGR方法的后缘噪声数值模拟[J]. 计算物理, 2011, 28(5): 698-704.
[7]	索奇峰, 吴晴, 钟易成, 李明水. 振动桥梁CFD数值模拟的网格运动算法[J]. 计算物理, 2011, 28(4): 547-553.
[8]	吴晴, 钟易成, 余少志, 胡骏. 基于LU-SGS的非结构弹簧网格迭代算法[J]. 计算物理, 2009, 26(6): 806-812.
[9]	成娟, 舒其望. 计算流体力学中的高精度数值方法回顾[J]. 计算物理, 2009, 26(5): 633-655.
[10]	王逸斌, 伍贻兆, 刘学强. 耦合辐射的三维热化学非平衡流数值模拟[J]. 计算物理, 2008, 25(4): 421-426.
[11]	招启军, 徐国华, 王适存. 基于CFD/Kirchhoff方法的直升机旋翼高速脉冲噪声模拟分析[J]. 计算物理, 2006, 23(2): 137-143.
[12]	汪建兵, 康宁. 粘性不可压流体流动问题用直角坐标网格的贴体解法[J]. 计算物理, 2004, 21(4): 290-298.
[13]	高智, 向华, 申义庆. 摄动有限体积法重构近似高精度的意义[J]. 计算物理, 2004, 21(2): 131-136.
[14]	白文, 刘国俊, 周天孝. 飞机构型Euler绕流结构网格方法计算的可信度[J]. 计算物理, 2000, 17(S1): 149-155.
[15]	吕晓斌, 兰黔章, 朱自强. 求解Euler方程的区域分解方法与并行算法[J]. 计算物理, 2000, 17(4): 360-366.