ITER具有内部输运垒方案中的离散阿尔芬本征模

doi:10.19596/j.cnki.1001-246x.8672

摘要/Abstract

摘要：

基于国际热核聚变实验堆(ITER)装置具有内部输运垒(ITB)的方案, 研究了离散阿尔芬本征模(αTAE)的物理特征, 其中α是等离子体压强梯度的标度参数。采用基于负离子的中性束注入(NNBI)加热和电流驱动能获得一个大且强的ITB以实现更高的性能, 并讨论该方案中αTAE的不稳定性。在纯射频方案中, 探究了ITB的收缩、维持和坍塌过程中的αTAE。模拟结果表明: αTAE发生于具有陡峭压强梯度的ITB区域, 形成的ITB越强会存在越多的αTAE, 且该模式的频率也越高。在高能量粒子条件下αTAE的多个分支容易变得不稳定, 被激发的αTAE其频率随着束能量的增加而增加。ITB作为高β_p方案的关键, 具有ITER稳态的许多理想特征, 因此关联性地探究了DIII-D高β_p方案中αTAE。

关键词: 阿尔芬本征模, 托卡马克, 等离子体不稳定性, 高能量粒子

Abstract:

The physical features of discrete Alfvén eigenmodes (αTAEs) bounded by the α-induced potential wells are investigated in ITER (International Thermonuclear Experimental Reactor) with the ITB (internal transport barrier) scenario, where α denotes a measure of the pressure gradient. The use of the negative-ion-based neutral beam injection (NNBI) heating and current driving can obtain a large and strong ITB for higher performance, and the instability of αTAE in this scheme is discussed. The αTAEs during sustaining, shrinking and erosion of ITB are discussed upon the pure radio frequency scenario. It is found that αTAEs exist in the ITB region due to the steep pressure gradient. More αTAEs exist in scenarios with strong ITB and the frequencies of these eigenmodes are higher. Multiple αTAEs are readily destabilized in the presence of energetic particles. The frequency of the excited αTAEs increases with increasing beam energy. The high β_p scenario with ITB on DIII-D has many of the desired properties of ITER steady-state. The αTAEs in high β_p scenarios are also studied.

Key words: Alfvén eigenmodes, tokamak, plasma instabilities, energetic particle

中图分类号:

TL631.24

欧阳思杰, 胡双辉, 欧阳学峰, 朱万坡, 兰源丹, 黄旋格. ITER具有内部输运垒方案中的离散阿尔芬本征模[J]. 计算物理, 2023, 40(6): 677-688.

Sijie OUYANG, Shuanghui HU, Xuefeng OUYANG, Wanpo ZHU, Yuandan LAN, Xuange HUANG. Discrete Alfvén Eigenmodes in ITER with the Internal Transport Barrier Scenario[J]. Chinese Journal of Computational Physics, 2023, 40(6): 677-688.

图/表 14

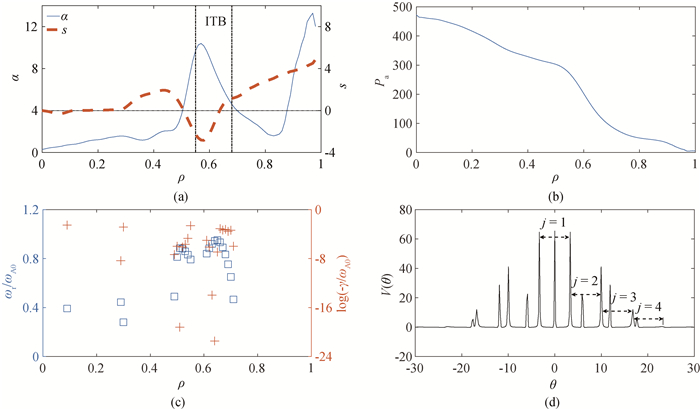
图1 (a)(s, α)参数和(b)压力沿ρ方向的剖面；(c)ωr/ωA0和log(-γ/ωA0)沿ρ方向的剖面分别用正方形(□)和加号(+)来表示；(d)为势阱结构

Fig.1 (a) The parameters (s, α) and (b) pressure profile versus ρ; (c) squares (□) and crosses (+) are used to describe ωr/ωA0 and log(-γ/ωA0) versus ρ, respectively; (d) structure of potential wells

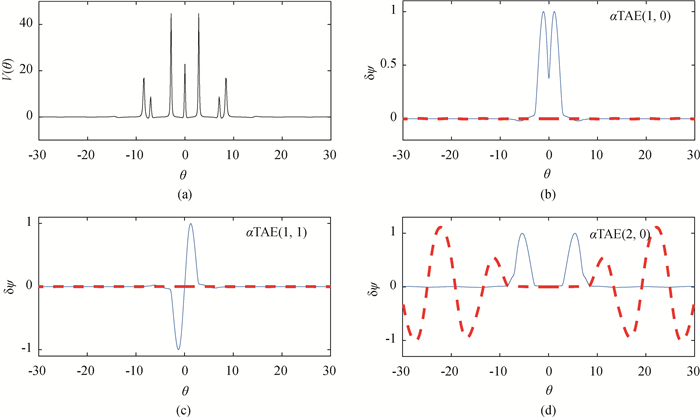
图2 (a) 势阱V以及MHD中s=0.61、α=5.98时的(b)(1, 0)模，(c)(1, 1)模，(d)(2, 0)模的模结构(图中δψ的实部和虚部分别用实线和虚线表示。)

Fig.2 (a) Potential V and (b) δψ(1, 0), (c) δψ(1, 1) and (d) δψ(2, 0) versus θ for α=5.98, s=0.61 in MHD (Real and imaginary δψ is plotted by solid and dashed line, respectively.)

图3 ρ=0.65，ωr/ωA0(—)和γ/ωA0(- - -)随kθρA0的变化

Fig.3 Real frequencies ωr/ωA0 (—) and growth rates γ/ωA0 (- - -) versus kθρA0 at ρ=0.65

图4 ρ=0.65，ωr/ωA0(—)和γ/ωA0(- - -)随vE/vA0的变化

Fig.4 Real frequencies ωr/ωA0 (—) and growth rates γ/ωA0 (- - -) versus vE/vA0 at ρ=0.65

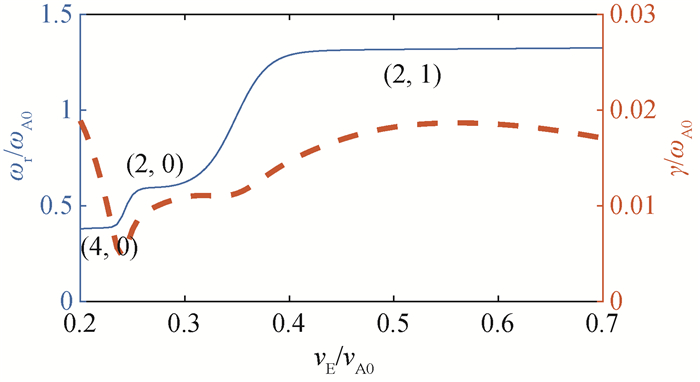
图5 ρ=0.65，θb∈[70°, 110°]，ωr/ωA0(—)和γ/ωA0(- - -)随vE/vA0的变化

Fig.5 Real frequencies ωr/ωA0 (—) and growth rates γ/ωA0 (- - -) versus vE/vA0 for θb∈[70°, 110°] at ρ=0.65

图6 ρ=0.65，ωr/ωA0(—)和γ/ωA0(- - -)随βE0的变化

Fig.6 Real frequencies ωr/ωA0 (—) and growth rates γ/ωA0 (- - -) versus βE0 at ρ=0.65

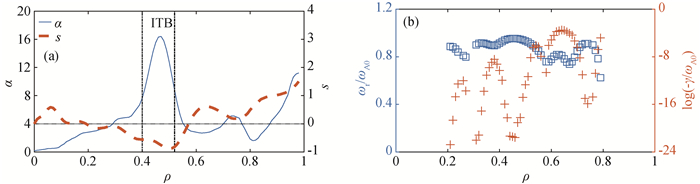
图7 (a) t=2 000 s，(s, α)参数沿着ρ方向的剖面；(b)ωr/ωA0和log(-γ/ωA0)沿着ρ方向的剖面，分别用正方形(□)和加号(+)表示

Fig.7 (a) The parameters (s, α) versus ρ at t=2 000 s; (b) Squares (□) and crosses (+) are used to describe the real frequencies ωr/ωA0 and the parameter relating to imaginary frequencies log(-γ/ωA0) versus ρ at t=2 000 s, respectively

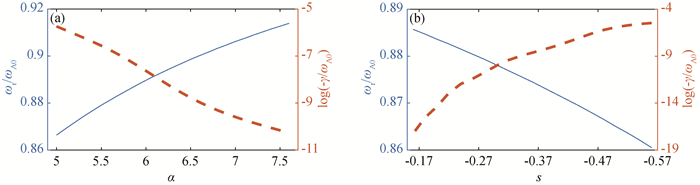
图8 (a) s=-0.56，ωr/ωA0和log(-γ/ωA0)随α的变化情况；(b)α=4.8，ωr/ωA0和log(-γ/ωA0)随s的变化情况(ωr/ωA0和log(-γ/ωA0)分别用实线(—)和虚线(-)表示。)

Fig.8 (a) Real frequencies ωr/ωA0 and the parameter relating to imaginary frequencies log(-γ/ωA0) versus α for s=-0.56; (b) ωr/ωA0 and log(-γ/ωA0) versus s for α=4.8 (ωr/ωA0and log(-γ/ωA0) are plotted by solid lines (—) and dashed lines (-), respectively.)

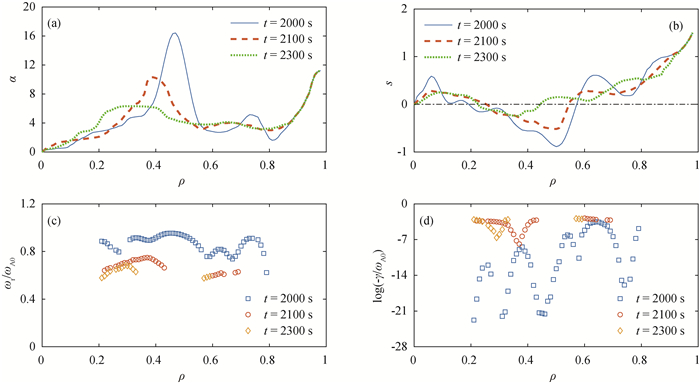
图9 (a) α和(b)s沿ρ方向的剖面；在t=2 000 s撤掉ECCD后(c)ωr/ωA0和(d)log(-γ/ωA0)沿着ρ的剖面

Fig.9 The parameters of (a) α and (b) s versus ρ; (c) real frequencies ωr/ωA0 and (d) the parameter relating to imaginary frequencies log(-γ/ωA0) versus ρ after the ECCD removed at t=2 000 s

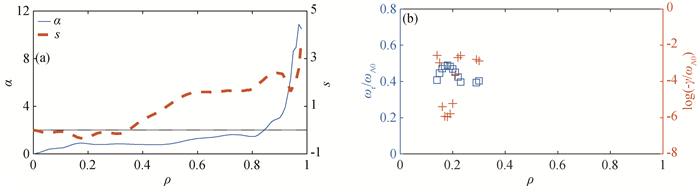
图10 在去除12 MW的ICH和LH系统和加入12 MW的NBI加热后，(a)t=2 300 s，(s, α)参数沿ρ方向的剖面和(b)t=2 300 s，αTAE沿ρ方向的发生区域(正方形(□)和加号(+)分别代表ωr/ωA0和log(-γ/ωA0)。)

Fig.10 After the addition of 12 MW of NBI heating by removing 12 MW of ICH and the LH system, (a) the parameters (s, α) versus ρ at t=2 300 s and (b) the range of αTAEs at t=2 300 s (Real frequencies ωr/ωA0 and the parameter relating to imaginary frequencies log(-γ/ωA0) are plotted by square (□) and crosses (+), respectively.)

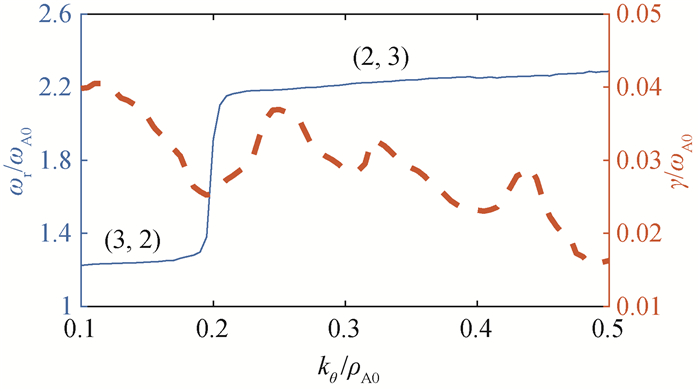
图11 t=2 000 s时，ρ=0.65处ωr/ωA0(—)和γ/ωA0(- - -)随kθρA0的变化

Fig.11 (a) Real frequencies ωr/ωA0 (—) and growth rates γ/ωA0 (- - -) versus kθρA0 at ρ=0.45 at t=2 000 s

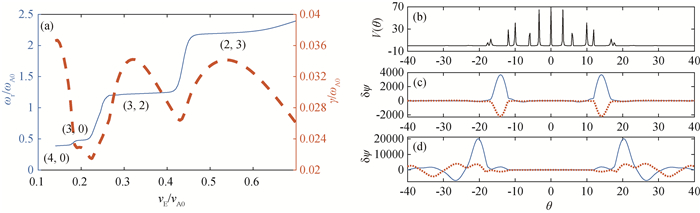
图12 t=2 000 s时，ρ=0.65处(a)ωr/ωA0(—)和γ/ωA0(- - -)随vE/vA0变化的情况；(b)势阱，混合模型下的αTAE；(c)(3, 0)模；(d)(4, 0)模

Fig.12 (a) Real frequencies ωr/ωA0 (—) and growth rate γ/ωA0 (- - -) versus vE/vA0 at ρ=0.45 at t=2 000 s; (b) potential well, (c) αTAEs (3, 0) and (d) (4, 0) verse θ in hybrid model

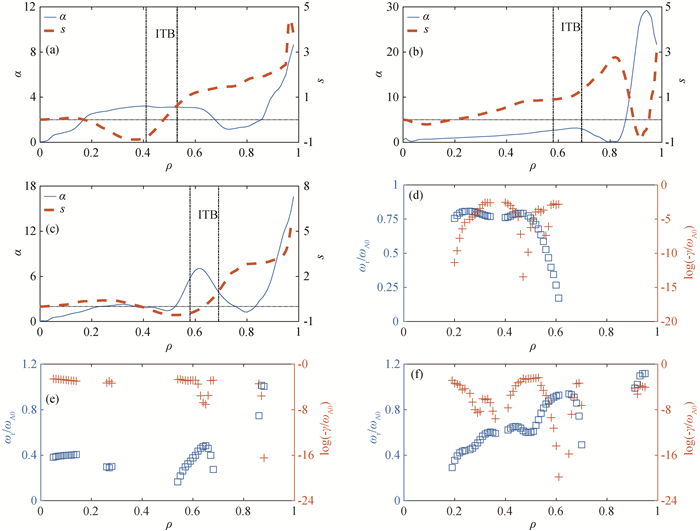
图13 (a)、(b)和(c)分别是方案1、方案2和方案3中(s, α)沿ρ方向的剖面；(d)、(e)和(f)分别是方案1、方案2和方案3中αTAE (1, 0)模沿ρ方向发生的区域(ωr/ωA0和log(-γ/ωA0)分别用正方形(□)和加号(+)表示。)

Fig.13 (a), (b) and (c) the parameters (s, α) versus ρ, corresponding to Case 1, Case 2 and Case 3; (d), (e) and (f) the frequency profiles of αTAE (1, 0), corresponding to Case 1, Case 2 and Case 3, respectively (Real frequencies ωr/ωA0 and the parameter relating to imaginary frequencies log(-γ/ωA0) are plotted by square (□) and crosses (+), respectively.)

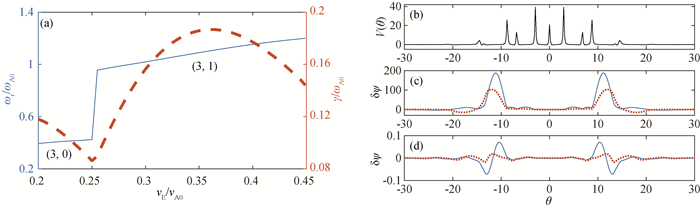
图14 方案3中，ρ=0.66, (a)ωr/ωA0(—)和γ/ωA0(- - -)随着vE/vA0变化的情况；(b)势阱；在混合模型下的αTAE(c)(3, 0)模和(d)(3, 1)模

Fig.14 In case 3, (a) real frequencies ωr/ωA0 (—) and growth rates γ/ωA0 (- - -) versus vE/vA0 at ρ=0.66; (b) potential well; (c) αTAE (3, 0) and (d) (3, 1) verse θ in hybrid model

参考文献 36

1	CHEN L . Theory of magnetohydrodynamic instabilities excited by energetic particles in Tokamaks[J]. Physics of Plasmas, 1994, 1 (5): 1519- 1522. DOI
2	CHENG C , CHEN L , CHANCE M . High-n ideal and resistive shear Alfvén waves in Tokamaks[J]. Annals of Physics, 1985, 161 (1): 21- 47. DOI
3	YANG W , LI G , HU Y , et al. Linear stability of toroidal Alfvén eigenmodes in the Chinese fusion engineering test reactor[J]. Fusion Engineering and Design, 2017, 114 (1): 118- 126.
4	ZHU X , WANG F , WANG Z . Nonlinear simulation of multiple toroidal Alfvén eigenmodes in tokamak plasmas[J]. Chinese Physics B, 2020, 29 (2): 025201. DOI
5	FU G , CHENG C . Theory of a high-n toroidicity-induced shear Alfvén eigenmode in tokamaks[J]. Physics of Fluids B: Plasma Physics, 1990, 2 (5): 985- 993. DOI
6	WEI S , WANG Y , SHI P , et al. Nonlinear coupling of reversed shear Alfvén eigenmode and toroidal Alfvén eigenmode during current ramp[J]. Chinese Physics Letters, 2021, 38 (3): 035201. DOI
7	CHEN W , YU L , LIU Y , et al. Destabilization of reversed shear Alfvén eigenmodes driven by energetic ions during NBI in HL-2A plasmas with q_min~1[J]. Nuclear Fusion, 2014, 54 (10): 104002. DOI
8	ZHANG T , LIU H , LI G , et al. Experimental observation of reverse-sheared Alfvén eigenmodes (RSAEs) in ELMy H-mode plasma on the EAST tokamak[J]. Plasma Science and Technology, 2018, 20 (11): 115101. DOI
9	WANG W , ZHOU D , HU Y , et al. Numerical simulation of the multiple reversed shear Alfvén eigenmodes associated with the triangularity Alfvén gap[J]. Chinese Physics B, 2018, 27 (12): 125202. DOI
10	HU S , CHEN L . Discrete Alfvén eigenmodes in high-β toroidal plasmas[J]. Physics of Plasmas, 2004, 11 (1): 1- 4. DOI
11	HU S , CHEN L . Discrete Alfvén eigenmodes excited by energetic particles in high-β toroidal plasmas[J]. Plasma Physics and Controlled Fusion, 2005, 47 (8): 1251- 1269. DOI
12	王帅, 龙超云, 胡双辉, 等. JET运行条件下高能量粒子激发的离散阿尔芬本征模[J]. 核聚变与等离子体物理, 2013, 33 (4): 301- 311.
13	孔冉, 胡双辉, 王帅, 等. JT-60U及JT-60SA运行条件下高能量粒子激发的离散阿尔芬本征模[J]. 核聚变与等离子体物理, 2013, 33 (2): 113- 120. DOI
14	王一如, 胡双辉, 姚龙宝, 等. DIII-D高性能运行参数下的离散阿尔芬本征模[J]. 核聚变与等离子体物理, 2012, 32 (2): 140- 147. DOI
15	WANG J , HU C , HU S , et al. Plasma science and technology, Alfvén instabilities excited by energetic particles in a parameter regime similar to EAST operation[J]. Plasma Science and Technology, 2013, 15 (8): 750- 754. DOI
16	WANG J , HU S , DAI Q , et al. Discrete Alfvén eigenmodes in international thermonuclear experimental reactor operations with negative magnetic shear[J]. Chinese Physics B, 2010, 19 (9): 095202. DOI
17	ZOU Y , CHAN V , HUANG J , et al. Validation of Alfvén eigenmode simulations on DIII-D and projection for CFETR scenario[J]. Nuclear Fusion, 2019, 59 (6): 066005. DOI
18	SHIMOMURA Y , MURAKAMI Y , POLEVOI A , et al. ITER: Opportunity of burning plasma studies[J]. Plasma Physics and Controlled Fusion, 2001, 43 (12A): A385- A394. DOI
19	SIPS A , GIRUZZI G , IDE S , et al. Progress in preparing scenarios for operation of the International Thermonuclear Experimental Reactor[J]. Physics of Plasmas, 2015, 22 (2): 021804. DOI
20	MURAKAMI M , PARK J , GIRUZZI G , et al. Integrated modelling of steady-state scenarios and heating and current drive mixes for ITER[J]. Nuclear Fusion, 2011, 51 (10): 103006. DOI
21	WOLF R . Internal transport barriers in tokamak plasmas[J]. Plasma Physics and Controlled Fusion, 2003, 45 (1): R1- R91. DOI
22	IDA K , FUJITA T . Internal transport barrier in tokamak and helical plasmas[J]. Plasma Physics and Controlled Fusion, 2018, 60 (3): 033001. DOI
23	VOITSEKHOVITCH I , GARBET X , BENKADD S , et al. Stabilization of ion temperature gradient driven turbulence and formation of an internal transport barrier in a tokamak[J]. Physics of Plasmas, 2002, 9 (11): 4671- 4684. DOI
24	JIAN G , HUANG L . The instability analysis of ion temperature gradient driven in a tokamak plasma with negative magnetic shear[J]. Chinese Journal of Computational Physics, 2001, 18 (6): 527- 530. DOI
25	LONG Y , MU Z , DONG J , et al. Numerical simulation and parallel efficiency of internal transport with barrier trigger in Tokamak plasmas[J]. Chinese Journal of Computational Physics, 2007, 24 (2): 141- 145.
26	LONG Y , MU Z , WANG A , et al. Numerical method for a kind of singular complex eigenequations[J]. Chinese Journal of Computational Physics, 2006, 23 (4): 436- 440. DOI
27	MCCLENAGHAN J , GAROFALO A , LAO L , et al. Transport at high β_p and development of candidate steady state scenarios for ITER[J]. Nuclear Fusion, 2020, 60 (4): 046025. DOI
28	GARCIA J , GIRUZZI G , ARTAUD J , et al. Integrated modeling of ITER steady-state scenarios[J]. Plasma Physics and Controlled Fusion, 2008, 50 (12): 124032. DOI
29	DING S , GAROFALO A , QIAN J , et al. Confinement improvement in the high poloidal beta regime on DIII-D and application to steady-state H-mode on EAST[J]. Physics of Plasmas, 2017, 24 (5): 056114. DOI
30	STAEBLER G , GAROFALO A , PAN C , et al. Transport barriers in bootstrap-driven tokamaks[J]. Physics of Plasmas, 2018, 25 (5): 056113. DOI
31	CONNOR J , HASTIE R , TAYLOR J . High mode number stability of an axisymmetric toroidal plasma transport barriers in bootstrap-driven tokamaks[J]. Proc R Soc Lond A, 1979, 365 (1720): 1- 17. DOI
32	CONNOR J , HASTIE R , TAYLOR J . Shear, periodicity, and plasma ballooning modes[J]. Physical Review Letters, 1978, 40 (6): 396- 399. DOI
33	CHEN L , HASEGAWA A . Kinetic theory of geomagnetic pulsations[J]. Journal of Geophysical Research, 1991, 96 (A2): 1503- 1512. DOI
34	PARKER S , LEE W . A fully nonlinear characteristic method for gyrokinetic simulation[J]. Physics of Fluids B: Plasma Physics, 1993, 5 (1): 77- 86. DOI
35	CHEN L , ZONCA F . Theory of shear Alfvén waves in toroidal plasma[J]. Physica Scripta, 1995, 1995 (T60): 81- 90.
36	ZHENG L , CHEN L , SANTORO R . Numerical simulations of toroidal Alfvén instabilities excited by trapped energetic ions[J]. Physics of Plasmas, 2000, 7 (6): 2469- 2476. DOI

[1]	朱万坡, 胡双辉, 欧阳学锋, 欧阳思杰, 兰源丹. EAST高约束运行条件下离散阿尔芬本征模的数值模拟[J]. 计算物理, 2023, 40(4): 461-472.
[2]	朱仁柱, 何家丰, 黄泰豪, 阮行磊, 徐宇晨, 郭晋, 刘天元, 毛世峰, 叶民友. 压力修正算法对刮削层等离子体输运方程数值求解性能的影响[J]. 计算物理, 2023, 40(1): 29-39.
[3]	郑书昱, 彭佳臻, 张先梅, 薛二兵, 虞立敏. 基于神经网络的托卡马克能量约束时间预测[J]. 计算物理, 2021, 38(4): 423-430.
[4]	刘祖光, 李新霞, 杨明. 低混杂波高N_‖分量对EAST等离子体电流驱动的影响[J]. 计算物理, 2020, 37(4): 467-472.
[5]	查学军, 钟德俊, 王福琼, 陈一平, 卢洪伟, 胡立群. EAST托卡马克杂质输运蒙特卡洛模拟[J]. 计算物理, 2015, 32(6): 715-721.
[6]	刘燕, 龚学余, 杨磊, 彭晓炜, 尹岚. 托卡马克中快波电流驱动下全波方程的数值求解[J]. 计算物理, 2012, 29(3): 375-382.
[7]	黄勤超, 王华忠, 罗家融, 袁旗平. EAST位形磁流体平衡的模拟[J]. 计算物理, 2006, 23(2): 231-236.
[8]	张先梅, 李有宜, 万宝年. 用MONTE CARLO方法计算托卡马克装置的中性氢原子密度分布[J]. 计算物理, 1999, 16(6): 606-609.
[9]	刘成安, 刘朝芬, 黄正丰, 刘忠兴. 聚变-裂变混合实验堆多维中子学的计算研究[J]. 计算物理, 1992, 9(3): 274-278.