碳纳米管内水吸附行为及等量吸附热的巨正则Monte Carlo模拟

doi:10.19596/j.cnki.1001-246x.8692

摘要/Abstract

摘要：

采用巨正则蒙特卡罗方法对单壁碳纳米管-水吸附体系进行计算模拟，通过对吸附和脱附等温线、局部密度分布、等量吸附热等进行表征，系统研究298 K时孔长、孔径以及表面强度对孔隙内水吸附行为的影响。结果表明：孔径效应对孔内水吸附行为影响显著，随着孔径逐渐增大，水分子先后以单链水、双链空心水环、水团簇的排列状态在孔内完成吸附。孔长在4~8 nm范围内时，随着孔长变大，发生吸附的初始压力越来越小，但当孔长增加到10 nm时，其对初始吸附压力的影响不再明显。最后，随着表面强度增大，发生水吸附的初始压力越来越小；同时，较小表面强度水分子的毛细蒸发相变过程瞬间完成，而当表面强度提高到40 K时，毛细蒸发相变过程则呈现出连续、逐渐完成的特点。

关键词: 碳纳米管, 吸附作用, 蒙特卡罗模拟, 等量吸附热, 相变

Abstract:

In this work, water adsorbed in single-walled carbon nanotube (SWCNT) is simulated by the Grand Canonical Monte Carlo (GCMC) method. The effects of pore length, pore size and surface strength on water adsorption behaviors at 298 K are systematically studied, via the characterization of isotherms, local density distribution and isosteric heat. There are hysteresis loops observed for water adsorbed and desorbed in SWCNTs with relatively large pore radii (PR=0.8, 1.0 nm), and the hysteresis loop disappears as the pore radius decreases to 0.55 nm. In addition, the water molecule packing manners are in the arrangement form of single chain, double helix chain and water clusters due to the pore size effects. When the pore length is in the range of 4~8 nm, the initial adsorption pressure becomes smaller and smaller as the pore length increases, but this effect rule gradually disappears with increasing pore length to 10 nm. Finally, the initial pressure of water adsorption decreases with surface strength; and when surface strengths are 20, 28, 32 K, the capillary evaporation phase transitions completed instantaneously. While the surface strength increases to 40 K, the capillary evaporation phase transition is shown gradually desorbed steps. As surface strengths increased from 20 K to 40 K, the isosteric adsorption heat at the pressure points of capillary condensation phase transition is 127.47, 117.98, 84.04, 59.16 kJ·mol^-1, respectively.

Key words: carbon nanotubes, adsorption, Monte Carlo simulation, isosteric adsorption heat, phase change

中图分类号:

TQ021.2

刘晨, 刘忠军, 赵明慧, 敖庆波. 碳纳米管内水吸附行为及等量吸附热的巨正则Monte Carlo模拟[J]. 计算物理, 2024, 41(2): 203-213.

Chen LIU, Zhongjun LIU, Minghui ZHAO, Qingbo AO. Grand Canonical Monte Carlo Simulation Study of Water Adsorption Behavior and Isosteric Adsorption Heat in Carbon Nanotubes[J]. Chinese Journal of Computational Physics, 2024, 41(2): 203-213.

图/表 9

图1 吸附体系模型示意图

Fig.1 Schematic diagram of adsorption system

表1 GCMC计算模拟中用到的势能模型参数

Table 1 Potential model parameters used in the GCMC simulations

Molecule		Molecule Parameters
Carbon^[23]		σ/nm	(ε/k_B)/k	ρ_s/nm^-2
Carbon^[23]		0.34	28.0	38.2
Water^[21]		σ/nm	(ε/k_B)/k	q/e
	O	0.316 6	78.23	-0.847 6
	H			0.423 8
		R_OM/nm	R_OH/nm	∠_HOH/°
		0.0	0.1	109.47

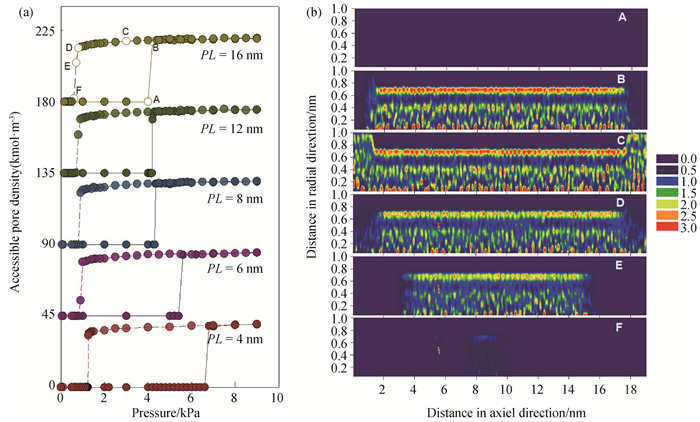
图2 (a) 298 K时孔半径1.0 nm、不同孔长SWCNT中的水吸附/脱附等温线; (为便于对比，PL=6、8、12、16 nm的等温线分别向上移动45、90、135、180。)(b)298 K时孔半径1.0 nm、孔长12 nm的SWCNT中水的局部密度分布图

Fig.2 (a) Isotherms of water adsorption and desorption in SWCNTs with pore radius of 1.0 nm and different pore lengths at 298 K; (To ease visualization, the isotherms of PL=6, 8, 12, 16 nm are shifted up by 45, 90, 135, 180, respectively.) (b) local density distributions of water adsorbed in 1.0 nm SWCNT with pore length of 12 nm at 298 K

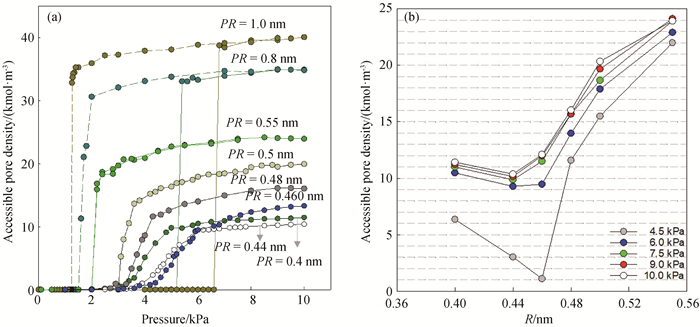
图3 (a) 298 K时，孔长为4.0 nm的不同孔径SWCNT中水吸附和脱附等温线；(为便于观察，PR=0.4、0.44、0.46、0.48、0.5 nm的SWCNT只给出了吸附支等温线。)(b)298 K时，不同吸附压力下SWCNT中水分子吸附量与孔径的关系

Fig.3 (a) Isotherms of water adsorption and desorption in SWCNTs with different pore radii and the pore length of 4 nm at 298 K; (For easy observation, SWCNT with PR=0.4, 0.44, 0.46, 0.48 and 0.5 nm only gives the isotherms of the adsorption branch.) (b) relations between pore densities of water adsorption and the pore radii of SWCNT at a series of pressures at 298 K

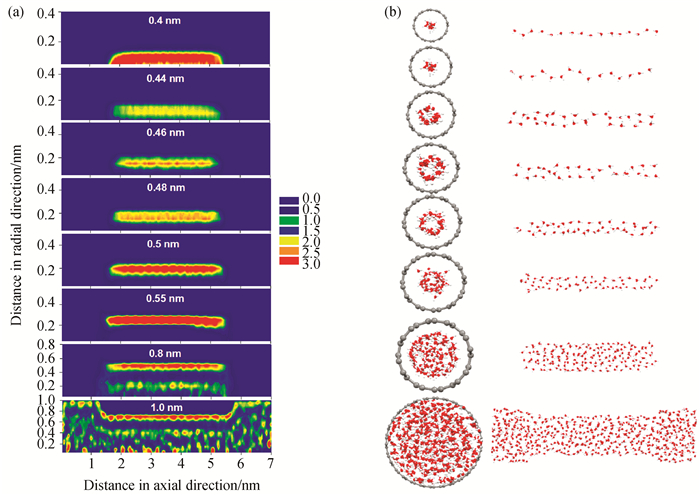
图4 (a) 298 K时、孔长为4 nm时的不同孔径SWCNT内水填充完成时的局部密度分布图；(b)与(a)对应条件下水吸附的瞬间构型图(孔半径由上至下依次为0.4、0.44、0.46、0.48、0.5、0.55、0.8、1.0 nm。)

Fig.4 (a) Local density distributions of water adsorbed in SWCNTs with different pore radii and pore length of 4 nm at 298 K; (b) the snapshots of water adsorption corresponding to the adsorption conditions in (a) (The pore radius is 0.4, 0.44, 0.46, 0.48, 0.5, 0.55, 0.8, and 1.0 nm from top to bottom.)

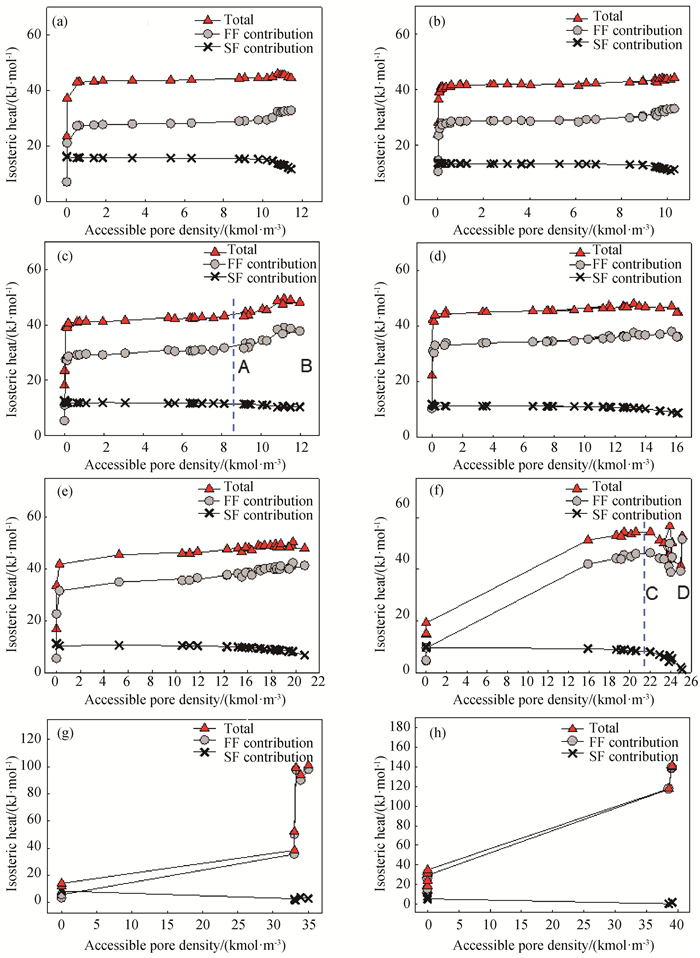
图5 298 K下，不同孔半径的SWCNT内水吸附的等量吸附热和可进入孔密度的关系(a) PR=0.4 nm；(b) PR=0.44 nm；(c) PR=0.46 nm；(d) PR=0.48 nm；(e) PR=0.5 nm；(f) PR=0.55 nm；(g) PR=0.8 nm；(h) PR=1.0 nm

Fig.5 Isosteric heats versus accessible pore density for water adsorption at 298 K in SWCNT with different pore radius (a) PR=0.4 nm; (b) PR=0.44 nm; (c) PR=0.46 nm; (d) PR=0.48 nm; (e) PR=0.5 nm; (f) PR=0.55 nm; (g) PR=0.8 nm; (h) PR=1.0 nm

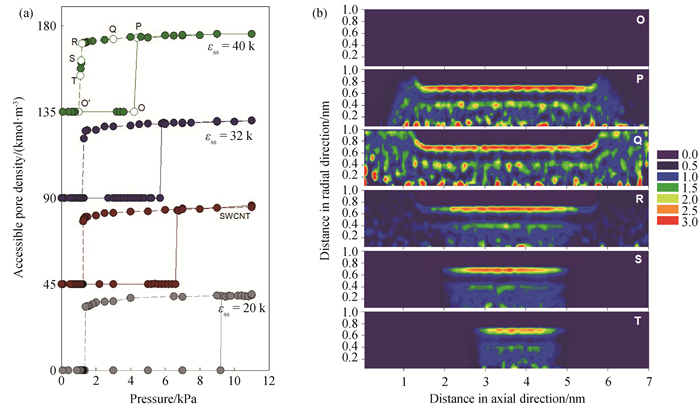
图6 (a) 298 K时孔半径为1.0 nm、孔长为4 nm、表面强度为20、28(SWCNT)、32、40 K的圆柱孔中的水吸附和脱附等温线; (为方便对比，SWCNT、εss=32、40 K的等温线分别向上移动45、90、135。)(b)表面强度为40 K时水吸附的局部密度分布图

Fig.6 (a) Isotherms of water adsorbed in tubes with pore radius of 1.0 nm, pore length of 4 nm and different surface strengths of 20, 28 (SWCNT), 32, 40 K at 298 K; (To ease visualization, the isotherms of SWCNT, εss=32, 40 K are shift up by 45, 90, 135 respectively.) (b) local density distributions of water adsorbed in pores with the surface strength of 40 K

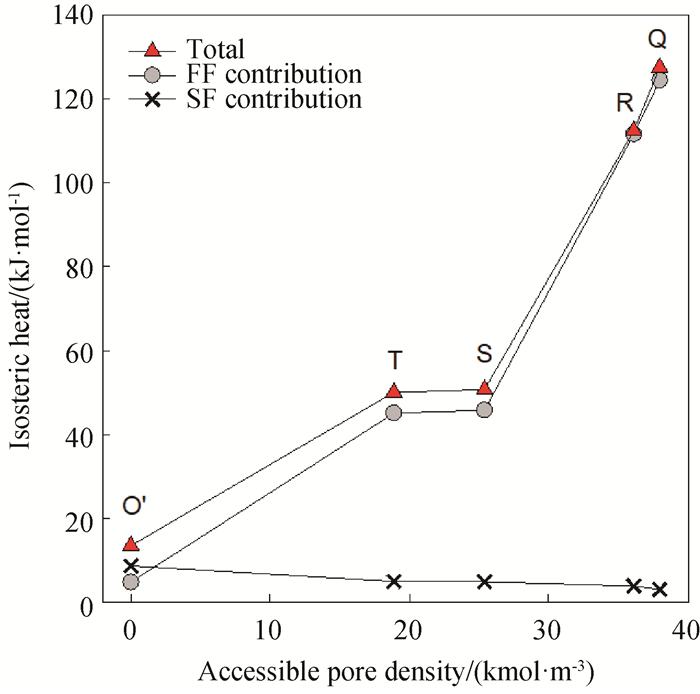
图7 298 K时孔半径为1.0 nm、孔长为4 nm、表面强度为40 K的水脱附等温线特殊压力点下的等量吸附热与可进入孔密度的关系

Fig.7 Isosteric heats at the pressures corresponding to the denoted points shown in 6(a) with the surface strength of 40 K at 298 K

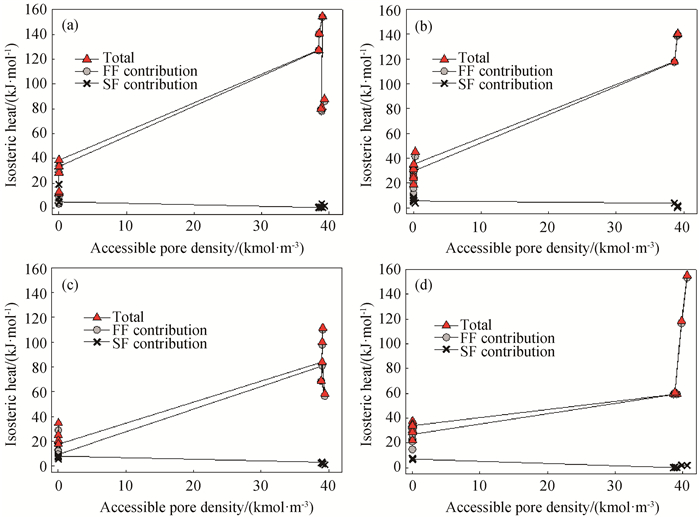
图8 298 K时不同表面强度的圆柱孔内水吸附等量吸附热与可进入孔密度的关系(a) εss=20 K；(b) SWCNT；(c) εss=32 K；(d) εss=40 K

Fig.8 Isosteric heats for water adsorption in cylindrical pores with different surface strengths at 298 K (a) εss=20 K; (b) SWCNT; (c) εss=32 K; (d) εss=40 K

参考文献 31

1	LIU L , ZENG W , TAN S J , et al. Microscopic insights into water adsorption in carbon nanopores-the role of acidic and basic functional groups and their configurations[J]. Phys Chem Phys, 2021, 23 (34): 18369- 18377. DOI
2	WANG C , XING Y , LEI Y , et al. Adsorption of water on carbon materials: The formation of "water bridge" and its effect on water adsorption[J]. Colloids and Surfaces A, 2021, 631, 127719. DOI
3	XU H , DO D D , NICHOLSON D . On the role of the quadrupole moment of carbon atom on water adsorption on graphite and in graphitic pores[J]. Chemical Engineering Journal, 2021, 409, 128236. DOI
4	SHI C , LIN C S , CHEN S , et al. Molecular dynamics simulation of characteristic water molecular arrangement on graphene surface and wetting transparency of graphene[J]. Acta Physica Sinica, 2019, 68 (8): 086801. DOI
5	HUANG Y , CHENG Q , WANG Z , et al. Competitive adsorption of benzene and water vapor on lignite-based activated carbon: Experiment and molecular simulation study[J]. Chemical Engineering Journal, 2020, 398, 125557. DOI
6	HORIKAWA T , YUASA R , YOSHIDA K , et al. Temperature dependence of water cluster on functionalized graphite[J]. Carbon, 2021, 183, 380- 389. DOI
7	OHBA T . Size-dependent water structures in carbon nanotubes[J]. Angew Chem Int Ed Engl, 2014, 53 (31): 8032- 8036. DOI
8	FARIMANI A B , ALURU N R . Spatial diffusion of water in carbon nanotubes: From fickian to ballistic motion[J]. J Phys Chem B, 2011, 115 (42): 12145- 12149. DOI
9	LIU B , SHI J Q , SHEN Y , et al. A molecular dynamics simulation of methane adsorption in graphite slit-pores[J]. Chinese Journal of Computational Physics, 2013, 30 (5): 692- 699.
10	HE M C , HU X X , ZHAO J . First-principles study of carbon monoxide adsorption liability on graphite (001)[J]. Chinese Journal of Computational Physics, 2016, 33 (6): 737- 742.
11	FENG L L , XU H T , WANG D , et al. Lattice Boltzmann simulation of formaldehyde adsorption by activated carbon[J]. Chinese Journal of Computational Physics, 2021, 38 (1): 69- 78.
12	WANG Y , DO D D , HERRERA L F , et al. On the condensation/evaporation pressures and isosteric heats for argon adsorption in pores of different cross-sections[J]. Colloids and Surfaces A, 2013, 420, 96- 102. DOI
13	TAN S J , PRASETYO L , DO D D , et al. On the growth of argon clusters on a weak adsorbent decorated with patches[J]. Colloid Interface Sci, 2019, 537, 431- 440. DOI
14	TAN S J , PRASETYO L , DO D D , et al. Interplay between wetting and filling of argon adsorption in slit pores with different surface energies transition from filling in micropores to capillary condensation in mesopores[J]. Ind Eng Chem Res, 2019, 58 (51): 23294- 23303. DOI
15	PRASETYO L , LOI Q K , TAN S J , et al. Effects of temperature on the transition from clustering to layering for argon adsorption on substrates of different strength-parametric map of wetting, pre-wetting and non-wetting[J]. Microporous and Mesoporous Materials, 2020, 304, 30648- 30656.
16	LOI Q K , XU H , DO D D , et al. On the description of argon adsorption on graphite for temperatures below the 2D-critical temperature[J]. Colloids and Surfaces A, 2021, 622, 126690. DOI
17	SONG W , YAO J , MA J , et al. Grand canonical Monte Carlo simulations of pore structure influence on methane adsorption in micro-porous carbons with applications to coal and shale systems[J]. Fuel, 2018, 215, 196- 203. DOI
18	LIU Y , WILCOX J . Effects of surface heterogeneity on the adsorption of CO₂ in microporous carbons[J]. Environ Sci Technol, 2012, 46 (3): 1940- 1947. DOI
19	CHIALVO A A , VLCEK L , CUMMINGS P T . Compounding effects of fluid confinement and surface strain on the wet-dry transition, thermodynamic response, and dynamics of water-graphene systems[J]. Molecular Physics, 2014, 113 (9-10): 1033- 1042.
20	NGUYEN P T M , DO D D , NICHOLSON D . On the hysteresis loop of argon adsorption in cylindrical pores[J]. The Journal of Physical Chemistry C, 2011, 115 (11): 4706- 4720. DOI
21	BERENDSEN H J C , GRIGERA J R , STRAATSMA T P . The missing term in effective pair potential[J]. Phys Chem, 1987, 91 (24): 6269- 6271. DOI
22	MAHONEY M W , JORGENSEN W L . A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions[J]. The Journal of Chemical Physics, 2000, 112 (20): 8910- 8922. DOI
23	STEELE W A . The physical interaction of gases with crystalline solids: Ⅰ. Gas-solid energies and properties of isolated adsorbed atoms[J]. Surface Science, 1973, 36 (1): 317- 352. DOI
24	PAN H , RITTER J A , BALBUENA P B . Examination of the approximations used in determining the isosteric heat of adsorption from the Clausius-Clapeyron equation[J]. Langmuir, 1998, 14 (21): 63230- 63277.
25	GARROD C . Statistical mechanics and thermodynamics[M]. New York: Oxford University Press, 1995: 622.
26	DO D D , DO H D , NICHOLSON D . Molecular simulation of excess isotherm and excell enthalpy change in gas-phase adsorption[J]. The Journal of Physical Chemistry B, 2009, 113 (4): 1030- 1040. DOI
27	GELB L D . The ins and outs of capillary condensation in cylindrical pores[J]. Molecular Physics, 2009, 100 (13): 2049- 2057.
28	赵明慧, 刘忠军, 姬帅, 等. 超临界氮气在单壁碳纳米管内吸附行为的GCMC模拟研究[J]. 物理学报, 2022, 71 (22): 12- 21.
29	DO D D , HERRERA LF , DO H D . A new method to determine pore size and its volume distribution of porous solids having known atomistic configuration[J]. Colloid Interface Sci, 2008, 328 (1): 110- 119. DOI
30	孙志伟, 何燕, 唐元政. 单壁碳纳米管受限空间内水的分布[J]. 物理学报, 2021, 70 (6): 151- 158.
31	EVERETT D H , POWL J C . Adsorption in slit-like and cylindrical micropores in the Henry's law region[J]. Journal of the Chemical Society, 1976, 72 (1): 619- 636.

[1]	付韬, 邬龙, 李晨光. 基于生成函数方法的现实网络座键渗流建模[J]. 计算物理, 2022, 39(2): 212-222.
[2]	杨波, 衷斌, 徐琪, 成立, 潘流俊, 沈华韵. (α, n)反应中子产额与能谱计算方法[J]. 计算物理, 2021, 38(4): 393-400.
[3]	王雪梅, 董斌, 朱子亮, 杨俊升. 聚合物分子与官能化纳米管相互作用及扩散特性的分子动力学模拟[J]. 计算物理, 2020, 37(5): 589-594.
[4]	王子墨, 李凌. 超短激光打孔中快速相变的格子玻尔兹曼模拟[J]. 计算物理, 2020, 37(3): 299-306.
[5]	魏志超, 王能平. 介质中双缺陷电荷对碳纳米管场效应晶体管量子输运特性的影响[J]. 计算物理, 2020, 37(3): 352-364.
[6]	李琼, 刘海风, 张弓木, 张其黎. 模拟退火算法在化学自由能模型中的应用[J]. 计算物理, 2019, 36(3): 259-264.
[7]	杨龙飞, 张业新, 都时禹. Matlab编程的Hückel分子轨道法计算研究掺杂纳米碳管的化学反应性[J]. 计算物理, 2017, 34(6): 685-696.
[8]	李胜强. 一种针对弱场搜寻态冷极性分子的可控静电表面囚禁方案[J]. 计算物理, 2017, 34(6): 731-739.
[9]	付元光, 郑建华, 上官丹骅, 李瑞, 李刚, 马彦, 邓力. 蒙特卡罗粒子输运软件JMCT的网格计数功能设计与实现[J]. 计算物理, 2016, 33(5): 581-586.
[10]	刘昌宇, 李仔武, 李栋. 含相变材料玻璃类围护结构传热系数分析[J]. 计算物理, 2016, 33(4): 427-433.
[11]	杨忠华, 刘贵立, 曲迎东, 李荣德. N掺杂碳纳米管环吸附Fe原子的第一性原理研究[J]. 计算物理, 2016, 33(3): 374-378.
[12]	吴海娜, 公卫江, 易光宇, 魏国柱. 纵向横向晶体场中自旋为1的量子伊辛二聚化链的基态[J]. 计算物理, 2015, 32(3): 374-378.
[13]	王伟, 张露, 李娜, 杨晓, 张婷, 岳工舒. 欠叠异质栅纳米碳管场效应管的量子输运特性[J]. 计算物理, 2015, 32(2): 229-239.
[14]	张旭辉, 郑委, 刘庆杰, 鲁晓兵. 裂隙多孔介质双重逾渗模型的算法实现[J]. 计算物理, 2014, 31(2): 191-199.
[15]	刘超, 石艺娜, 秦承森, 梁仙红. α铁冲击相变的离散元方法[J]. 计算物理, 2014, 31(1): 51-58.