基于混合算法的P-SV波叠前反演

doi:10.19596/j.cnki.1001-246x.8730

摘要/Abstract

摘要：

根据P-SV波反射系数近似公式, 建立关于各向异性参数的反演目标函数, 分别使用单一算法和混合算法实现TTI介质各向异性参数的反演, 结果表明: 混合算法反演精度更高, 过程更稳定; 进一步, 对理论模型数据加信噪比为5的高斯白噪声, 对抗噪性进行测试, 反演结果的误差较小, 抗噪能力较好。最后对改造后的Hess模型进行各向异性参数反演, 得到反演剖面, 与原始剖面吻合度较高, 验证了混合算法的有效性; 选取研究区, 对实际资料进行反演测试, 得到的反演效果较好, 精确度较高, 验证了混合算法在实际应用中的有效性。

关键词: 遗传算法, 模拟退火法, 混合算法, 转换波, 叠前反演

Abstract:

The simulated annealing method is introduced into genetic algorithm to form a hybrid algorithm, which can overcome the defects of genetic algorithm in optimization and avoid the premature phenomenon. According to the approximate formula of reflection coefficient of P-SV wave, the objective function of anisotropy parameter inversion is established. The anisotropy parameter inversion of TTI medium is achieved by using single algorithm and mixed algorithm respectively. The results show that the mixed algorithm inversion accuracy is higher and the process is more stable. Furthermore, Gaussian white noise with a signal-to-noise ratio of 5 is added to the data of the theoretical model to test the anti-noise property. The error of the inversion results is small and the anti-noise ability is good. Finally, the anisotropic parameter inversion of the modified Hess model is carried out, and the inversion profile is obtained, which is in good agreement with the original profile, and the effectiveness of the hybrid algorithm is verified. In addition, the research area is selected to perform inversion test on the actual data. The inversion results are good and the accuracy is high, which verifies the effectiveness of the hybrid algorithm in practical application.

Key words: genetic algorithm, simulated annealing method, hybrid algorithm, converted wave, prestack inversion

中图分类号:

P631

李勤, 张敏, 许莹. 基于混合算法的P-SV波叠前反演[J]. 计算物理, 2024, 41(3): 380-391.

Qin LI, Min ZHANG, Ying XU. P-SV Wave Prestack Inversion Based on Hybrid Algorithm[J]. Chinese Journal of Computational Physics, 2024, 41(3): 380-391.

图/表 18

图1 模拟退火算法搜索最优解示意图

Fig.1 Schematic of simulated annealing algorithm searching for optimal solution

表1 三组两层介质模型参数

Table 1 Model parameters of three sets of two-layer media

介质结构	ε	δ	γ	θ₂	φ
ISO/TTI	0/0.2	0/0.1	0/0.11	0/60	0/30
TTI/ISO	0.2/0	0.1/0	0.11/0	60/0	30/0
TTI/TTI	0.1/0.2	0.1/0.1	0.15/0.11	45/60	30/45

图2 不同介质模型近似反射系数

Fig.2 Approximate reflection coefficients of the medium models

表2 两层介质模型的各向异性参数

Table 2 Anisotropic parameters of two-layer medium model

介质结构	ε	δ	γ	θ₂	φ
	0.1~0.4	0.1	0.11
ISO/TTI	0.2	0.05~0.2	0.11	0/60	0/30
	0.2	0.1	0.06~0.21
	0.1~0.4	0.1	0.11
TTI/ISO	0.2	0.05~0.2	0.11	60/0	30/0
	0.2	0.1	0.06~0.21
	0.1~0.4	0.1	0.11
TTI/TTI	0.2	0.05~0.2	0.11	45/60	30/45
	0.2	0.1	0.06~0.21

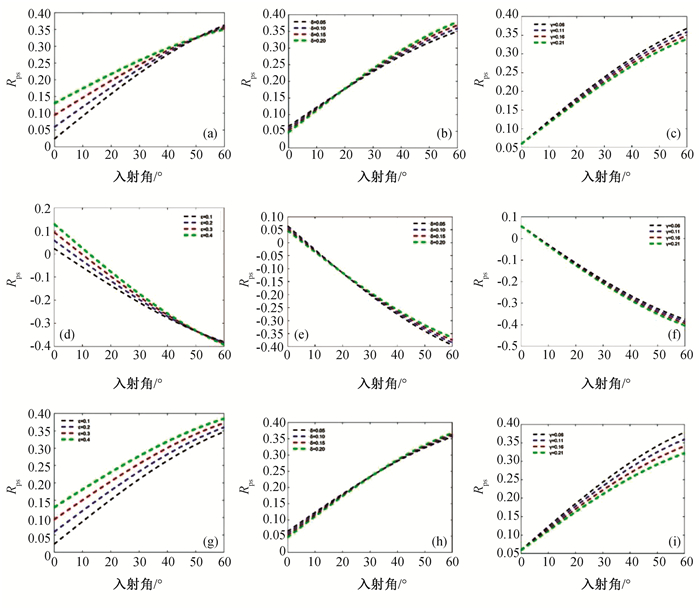
图3 三组模型中各向异性参数ε, δ, γ对RPS的影响(a) ISO/TTI(ε); (b) ISO/TTI(δ); (c) ISO/TTI(γ); (d) TTI/ISO(ε); (e) TTI/ISO(δ); (f) TTI/ISO(γ); (g) TTI/TTI(ε); (h) TTI/TTI(δ); (i) TTI/TTI(γ)

Fig.3 Effects of anisotropic parameters ε, δ, γ on RPS in three models (a) ISO/TTI(ε); (b) ISO/TTI(δ); (c) ISO/TTI(γ); (d) TTI/ISO(ε); (e) TTI/ISO(δ); (f) TTI/ISO(γ); (g) TTI/TTI(ε); (h) TTI/TTI(δ); (i) TTI/TTI(γ)

表3 ISO/TTI介质模型参数

Table 3 ISO/TTI media model parameters

介质	V_P/(m·s^-1)	V_S/(m·s^-1)	ρ/(g·cm^-3)	ε	δ	γ	θ₂	φ
ISO	3 000	1 750	2.4	0	0	0	0	0
TTI	2 900	1 650	2.6	0.43	0.35	0.11	60	30

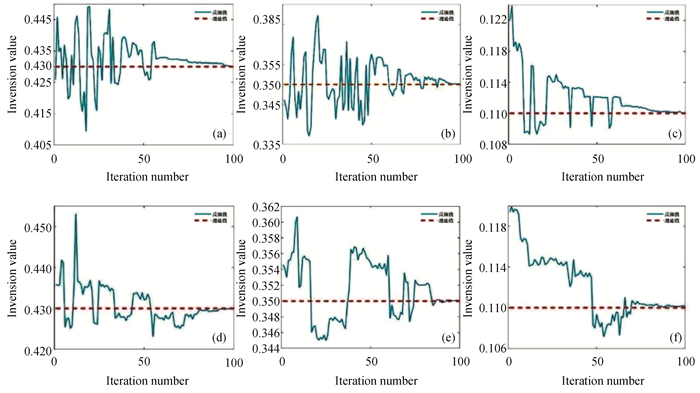
图4 TTI介质P-SV波单一算法参数ε, δ, γ反演(a) GA (ε); (b) GA (δ); (c) GA (γ); (d) SA (ε); (e) SA (δ); (f) SA (γ)

Fig.4 TTI medium P-SV wave inversion by single algorithm with ε, δ, γ (a) GA (ε); (b) GA (δ); (c) GA (γ); (d) SA (ε); (e) SA (δ); (f) SA (γ)

表4 TTI介质各向异性参数反演结果(GA, SA)

Table 4 Anisotropy parameter inversion results in TTI medium (GA, SA)

反演参数	GA			SA
反演参数	ε	δ	γ	ε	δ	γ
理论值	0.430	0.350	0.110	0.430	0.350	0.110
反演值	0.432	0.339	0.106	0.430 7	0.351 4	0.112
相对误差/%	0.469	3.143	3.290	0.166	0.408	1.950

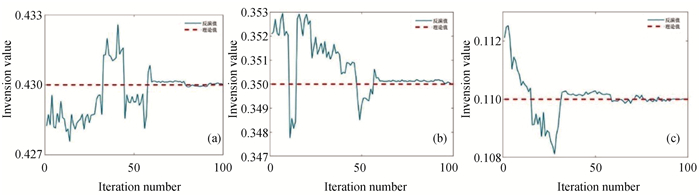
图5 TTI介质P-SV波混合算法反演ε, δ, γ (a) HGA(ε); (b) HGA(δ); (c)HGA(γ)

Fig.5 TTI medium P-SV wave inversion by hybrid algorithm with ε, δ, γ (a) HGA(ε); (b) HGA(δ); (c)HGA(γ)

表5 TTI介质各向异性参数反演结果(HGA)

Table 5 Anisotropy parameter inversion results in TTI medium (HGA)

	ε	δ	γ
理论值	0.430 0	0.350 0	0.110 0
反演值	0.429 6	0.350 6	0.110 6
相对误差/%	0.080 9	0.185 7	0.536 0

图6 信噪比为5 dB的高斯白噪声的角道集

Fig.6 Corner track set of white Gaussian noise with signal to noise ratio of 5 dB

表6 加噪声的TTI介质各向异性参数反演结果

Table 6 Inversion results of anisotropy parameters in TTI media with noise

	ε	δ	γ
理论值	0.430	0.350	0.110
反演值	0.452	0.313	0.119
相对误差/%	5.116	10.571	8.181

表7 N=50，100，T=100时，遗传算法、模拟退火法、混合算法反演结果

Table 7 With N = 50 or 100, T = 100, inversion results of genetic algorithm, simulated annealing algorithm and hybrid genetic algorithm

反演参数	GA		SA		HGA
反演参数	N=50	N=100	N=50	N=100	N=50	N=100
A/%	1.132	0.233	3.257	4.298	2.182	0.573
B/%	2.571	1.577	0.637	1.566	1.595	1.771
C/%	4.590	1.682	8.496	3.980	3.612	1.305

表8 T=50，150，N=80时，遗传算法、模拟退火法、混合算法反演结果

Table 8 With T = 50 or 100, N=80, inversion results of genetic algorithm, simulated annealing algorithm and hybrid genetic algorithm

反演参数	GA		SA		HGA
反演参数	T=50	T=150	T=50	T=150	T=50	T=150
A/%	0.264	0.256	3.488	4.235	0.343	0.003
B/%	1.103	0.409	0.192	1.514	1.218	1.761
C/%	0.349	3.490	2.410	2.563	2.727	0.666

图7 Hess-TTI介质模型及反演区域

Fig.7 Hess-TTI medium model and inversion region

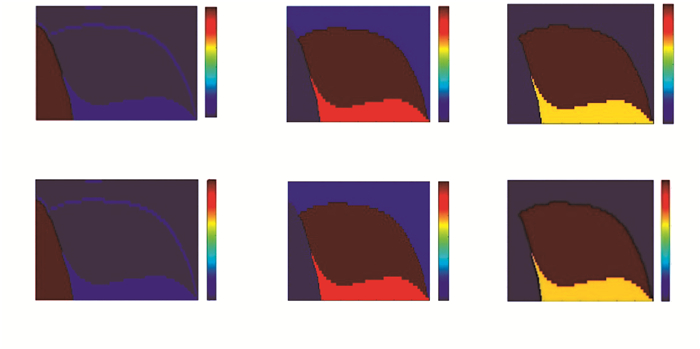
图8 Hess-TTI模型各向异性参数剖面(右侧颜色栏表示各向异性参数区间。)(a) ε原始剖面；(b) δ原始剖面；(c) γ原始剖面；(d) ε反演剖面；(e) δ反演剖面；(f) γ反演剖面

Fig.8 Profile of anisotropy parameters of the Hess-TTI model (Color bar on the right represents interval of anisotropy parameter.) (a) ε original profile; (b) δ original profile; (c) γ original profile; (d) ε inversion profile; (e) δ inversion profile; (f) γ inversion profile

图9 所选研究区块数据资料(a) 波阻抗反演剖面；(b) 合成角道集

Fig.9 Selected study block data (a) wave impedance inversion profile; (b) synthetic corner track set

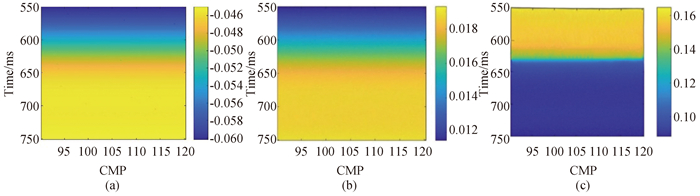
图10 实际数据资料各向异性参数反演剖面(右侧颜色栏表示各向异性参数区间。) (a) ε反演剖面；(b) δ反演剖面；(c) γ反演剖面

Fig.10 Anisotropy parameter inversion profile of actual data (Color bar on the right represents interval of anisotropic parameter.) (a) ε inversion profile; (b) δ inversion profile; (c) γ inversion profile

参考文献 48

1	强敏, 段志强, 张吉, 等. P-P、P-SV波叠前联合反演在致密气储层预测中的应用[J]. 地球物理学进展, 2018, 33 (4): 1540- 1544.
2	张凌远, 张宏兵, 尚作萍, 等. 基于Zoeppritz方程的叠前和叠后混合多参数非线性地震反演[J]. 石油地球物理勘探, 2021, 56 (1): 164- 171.
3	李爱山, 印兴耀, 张繁昌, 等. 叠前AVA多参数同步反演技术在含气储层预测中的应用[J]. 石油物探, 2007, 46 (1): 64-68, 93. DOI
4	喻岳钰, 杨长春, 王彦飞, 等. 叠前弹性阻抗反演及其在含气储层预测中的应用[J]. 地球物理学进展, 2009, 24 (2): 574- 580. DOI
5	张卫卫, 何敏, 颜承志, 等. AVO叠前反演技术在珠江口盆地白云深水区烃类检测中的应用[J]. 中国海上油气, 2010, 22 (3): 160-163, 167. DOI
6	郎晓玲, 彭仕宓, 康洪全, 等. 叠前同时反演方法在流体识别中的应用[J]. 石油物探, 2010, 49 (2): 164- 169. DOI
7	周义军, 蒲仁海, 曾令帮. 叠前储层描述技术在岩性气藏勘探中的研究与应用[J]. 地球物理学进展, 2011, 26 (1): 229- 234. DOI
8	刘涛, 方中于, 但志伟, 等. 叠前同步反演在涠西南凹陷储层预测中的应用[J]. 石油天然气学报, 2011, 33 (9): 77- 81. DOI
9	施行觉, 夏从俊, 吴永钢. 储层条件下波速的变化规律及其影响因素的实验研究[J]. 地球物理学报, 1998, 41 (2): 234- 241. DOI
10	阴可, 杨慧珠. 各向异性介质中的AVO[J]. 地球物理学报, 1998, 41 (3): 382- 391. DOI
11	DONATE M S , MARTIN N W . Making AVO analysis for converted waves a practical issue[J]. SEG Technical Program Expanded Abstracts, 1998, 17, 2060- 2063.
12	ALVAREZ K , DONATE M , ALDANA M . AVO analysis for converted waves[J]. SEG Technical Program Expanded Abstracts, 1999, 18, 876- 879.
13	NEFEDKINA T , BUZLUKOV V . Seismic dynamic inversion using multiwave AVO-data[J]. SEG Technical Program Expanded Abstracts, 1999, 18, 888- 891.
14	PŠENČÍK I , VAVRYČUK V . Weak contrast PP wave displacement R/T coefficients in weakly anisotropic elastic media[J]. Pure and Applied Geophysics, 1998, 151 (2/4): 699- 718.
15	VAVRYČUK V . Weak-contrast reflection/transmission coefficients in weakly anisotropic elastic media: P-wave incidence[J]. Geophysical Journal International, 1999, 138 (2): 553- 562. DOI
16	JÍLEK P . Converted PS-wave reflection coefficients in weakly anisotropic media[J]. Pure and Applied Geophysics, 2002, 159 (7/8): 1527- 1562.
17	ARTOLA F V A , LEIDERMAN R , FONTOURA S A B , et al. Zero-offset C-wave reflectivity in horizontally layered media[J]. SEG Technical Program Expanded Abstracts, 2003, 22, 761- 764.
18	BEHURA J , TSVANKIN I . Small-angle AVO response of PS-waves in tilted TI media[J]. SEG Technical Program Expanded Abstracts, 2005, 24, 206- 209.
19	MALLICK S . Model-based inversion of amplitude-variations-with-offset data using a genetic algorithm[J]. Geophysics, 1995, 60 (4): 939- 954. DOI
20	SEN M K , STOFFA P L . Simulated annealing, genetic algorithms and seismic waveform inversion[J]. SEG Technical Program Expanded Abstracts, 1991, 10, 945- 947.
21	STOFFA P L , SEN M K . Nonlinear multiparameter optimization using genetic algorithms; inversion of plane-wave seismograms[J]. Geophysics, 1991, 56 (11): 1794- 1810. DOI
22	方中于, 王丽萍, 杜家元, 等. 基于混合智能优化算法的非线性AVO反演[J]. 石油地球物理勘探, 2017, 52 (4): 797- 804.
23	成琥, 赵宪生, 王红霞, 等. 基于BP网络和遗传算法的波阻抗混合反演[J]. 石油物探, 2006, 45 (6): 574- 579. DOI
24	聂茹, 岳建华, 邓帅奇. 地震波阻抗反演的免疫粒子群算法[J]. 中国矿业大学学报, 2010, 39 (5): 733- 739.
25	徐善辉, 韩立国, 郭建. TTI介质各向异性参数多波反演与PS波AVO分析[J]. 地球物理学报, 2012, 55 (2): 569- 576.
26	王丽萍. 智能优化算法叠前AVO非线性反演研究[D]. 武汉: 中国地质大学, 2015.
27	METROPPOLIS N , ROSENBLUTH A W , ROSENBLUTH M N , et al. Equation of state calculations by fast computing machines[J]. The Journal of Chemical Physics, 1953, 21 (6): 1087- 1092. DOI
28	KIRKPATRIEK S , CELATT C D , VECCHI M P . Optimization by simulated annealing[J]. Science, 1983, 220 (4598): 671- 680. DOI
29	ROTHMAN D H . Nonlinear inversion, statistical mechanics, and residual statics estimation[J]. Geophysics, 1985, 50 (12): 2784- 2796. DOI
30	ROTHMAN D H . Automatic estimation of large residual statics corrections[J]. Geophysics, 1986, 51 (2): 332- 346. DOI
31	SEN M K , STOFFA P L . Nonlinear one-dimensional seismic waveform inversion using simulated annealing[J]. Geophysics, 1991, 56 (10): 1624- 1638. DOI
32	SEND M K , BHATTACHARYA B B , STOFFA P L . Nonlinear inversion of resistivity sounding data[J]. Geophysics, 1993, 58 (4): 496- 507. DOI
33	MA Xinquan . Simultaneous inversion of prestack seismic data for rock properties using a global simulated annealing[J]. Geophysics, 2002, 67 (6): 1877- 1885. DOI
34	任义庆, 徐仲达, 马在田. 应用模拟退火法反演横波速度[J]. 石油地球物理勘探, 1996, 31 (5): 677- 684.
35	师学明, 王家映. 一维层状介质大地电磁模拟退火反演法[J]. 地球科学, 1998, 23 (5): 543- 545.
36	桂卫华, 黄泰松, 阳春华. 一种改进遗传算法及其在企业原料采购优化中的应用[J]. 矿冶工程, 2001, 21 (3): 59- 62. DOI
37	吴浩扬, 常炳国, 朱长纯, 等. 基于模拟退火机制的多种群并行遗传算法[J]. 软件学报, 2000, 11 (3): 416- 420.
38	李勤, 赵斌, 马随波. TTI煤层群、相速度分析[J]. 计算物理, 2020, 37 (6): 709- 717.
39	倪小威, 徐思慧, 冯加明, 等. 基于自适应差分进化算法的阵列侧向测井快速反演[J]. 计算物理, 2019, 36 (4): 465- 473.
40	王黎翔, 王安琪, 黄志祥. 基于多算法优化SVM的粗糙面参数反演[J]. 计算物理, 2019, 36 (5): 577- 585.
41	杨练兵, 郑宏伟, 罗格平, 等. 基于遗传算法优化BP神经网络的土壤盐渍化反演[J]. 地理与地理信息科学, 2021, 37 (2): 12-21, 37. DOI
42	萧秋兰. 遗传模拟退火算法的优化研究[J]. 信息记录材料, 2022, 23 (12): 95- 98. DOI
43	李琼, 刘海风, 张弓木, 等. 模拟退火算法在化学自由能模型中的应用[J]. 计算物理, 2019, 36 (3): 259- 264.
44	KANG Zhou, QU Zhiyi. Application of BP neural network optimized by genetic simulated annealing algorithm to prediction of air quality index in Lanzhou[C]//2017 2nd IEEE International Conference on Computational Intelligence and Applications (ICCIA). Beijing, China: IEEE, 2017: 155-160.
45	印兴耀, 刘婵娟, 王保丽. 基于混合遗传算法的叠前随机反演方法[J]. 中国石油大学学报(自然科学版), 2017, 41 (4): 65- 70. DOI
46	李政伟, 谭国俊. 改进的退火遗传优化策略应用研究[J]. 计算机工程与应用, 2010, 46 (4): 245- 248. DOI
47	徐善辉. TTI介质PS波小角度AVO分析[D]. 长春: 吉林大学, 2009.
48	宋欢, 胡耀垓, 赵正予, 等. 基于混合遗传算法的斜测电离图参数反演[J]. 地球物理学报, 2014, 57 (3): 703- 714.

[1]	韩文敏, 戴耀东, 姚初清, 田家祥, 蒋丹枫, 周一帆. 遗传算法在中子-γ混合辐射场屏蔽材料优化设计中的应用[J]. 计算物理, 2024, 41(3): 357-366.
[2]	丁永龙, 胡琳萍, 张瑞勤. 一种基于迭代子空间直接求逆算法的高效子空间混合算法[J]. 计算物理, 2021, 38(4): 418-422.
[3]	屠丽娟, 周恩泽, 吴雪飞, 杨琪, 丁雪峰. 基于流量测点的热网变动阻力系数优化辨识[J]. 计算物理, 2021, 38(4): 498-504.
[4]	颜帆, 卢玫. 材料热物性与热源强度辨识的改进遗传算法[J]. 计算物理, 2015, 32(5): 623-630.
[5]	田炜, 任新成, 郭立新. 分形分层粗糙面电磁波透射特性的混合算法[J]. 计算物理, 2013, 30(1): 134-139.
[6]	邢小宁, 井西利, 马毅恒, 王全志, 许耀芸. 自适应混合遗传算法优化团簇[J]. 计算物理, 2012, 29(3): 459-465.
[7]	张帅, 龚书喜, 关莹, 龚琦. 大型平面阵列天线辐射方向图的小阵外推计算和综合方法[J]. 计算物理, 2011, 28(4): 554-560.
[8]	任师波, 韩鹏, 杨冠玲. 用于光子相关光谱颗粒粒度测量的实数编码混合遗传算法[J]. 计算物理, 2011, 28(1): 87-93.
[9]	李绍新. 动态光散射测量粒径分布的格雷码编码遗传算法反演运算[J]. 计算物理, 2008, 25(3): 323-329.
[10]	常珊, 孔韧, 李春华, 陈慰祖, 王存新. 基于MPI的分子对接并行算法[J]. 计算物理, 2008, 25(2): 241-246.
[11]	范小平, 李功胜. 确定地下水污染强度的一种改进的遗传算法[J]. 计算物理, 2007, 24(2): 187-191.
[12]	陈金春. Rh_n(n=2~20)团簇结构和磁特性[J]. 计算物理, 2005, 22(5): 437-443.
[13]	姚磊华. 用改进的遗传算法和高斯牛顿法联合反演三维地下水流模型参数[J]. 计算物理, 2005, 22(4): 311-318.
[14]	刘洪亮, 赵逸琼, 李永平, 付绍军, 张巍, 张晓波, 舒方杰. 一种用于均匀照明的衍射光学元件设计的快速模拟退火法[J]. 计算物理, 2005, 22(3): 240-244.
[15]	詹浩, 白俊强, 段卓毅, 华俊. 基于遗传算法和分布式计算的气动优化设计[J]. 计算物理, 2004, 21(4): 359-362.