计算物理 ›› 2024, Vol. 41 ›› Issue (1): 98-109.DOI: 10.19596/j.cnki.1001-246x.8791
• 面向超级计算机的性能优化技术与数值并行算法专刊 • 上一篇 下一篇
冯春生1,2( ), 李仕哲3, 刘生豪1, 张晨松3,*(
), 李仕哲3, 刘生豪1, 张晨松3,*( ), 赵梨1
), 赵梨1
收稿日期:2023-07-01
出版日期:2024-01-25
发布日期:2024-02-05
通讯作者:
张晨松
作者简介:冯春生, 男, 博士, 教授, 博士生导师, 研究方向为油藏数值模拟、并行计算, E-mail: spring@xtu.edu.cn
基金资助:
Chunsheng FENG1,2( ), Shizhe LI3, Shenghao LIU1, Chensong ZHANG3,*(
), Shizhe LI3, Shenghao LIU1, Chensong ZHANG3,*( ), Li ZHAO1
), Li ZHAO1
Received:2023-07-01
Online:2024-01-25
Published:2024-02-05
Contact:
Chensong ZHANG
摘要:
渗流力学模型由多个偏微分方程非线性耦合而成。在不同的应用问题中, 渗流力学问题的特性并不完全相同, 相应的求解方法也不相同。本文以油气藏开发中的典型数学模型为例, 介绍多孔介质中的多相多组分渗流力学方程的数学形式、应用特征以及其离散线性方程组的高效求解方法, 特别是一些常用的预条件方法。此外, 对标准算例进行适当的修改, 对部分预条件方法的共享内存并行效率进行了测试。
中图分类号:
冯春生, 李仕哲, 刘生豪, 张晨松, 赵梨. 面向渗流力学应用特征的预条件方法[J]. 计算物理, 2024, 41(1): 98-109.
Chunsheng FENG, Shizhe LI, Shenghao LIU, Chensong ZHANG, Li ZHAO. Application-oriented Preconditioning of Seepage Mechanics[J]. Chinese Journal of Computational Physics, 2024, 41(1): 98-109.
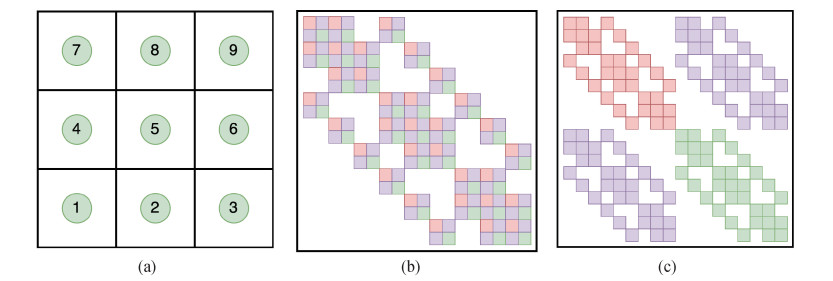
图1 2种自由度排序方式下的块稀疏矩阵非零结构示意图(a) 二维网格示意图(一个网格单元有2个自由度。); (b) 网格优先排序; (c) 物理量优先排序的稀疏矩阵块结构
Fig.1 Schematic diagram of non-zeros structure of block sparse matrix for the two degrees of freedom sorting methods (a) 2D gridschematic diagram (A grid element has 2 degrees of freedom.); (b) sparse matrix block structure of grid prioritization; (c) sparse matrix block structure of physical quantities prioritization
| 解法器 | CPR-FGMRES(30) | ||||
| 线程数 | 1 | 2 | 4 | 8 | 16 |
| 时间步数 | 53 | 53 | 53 | 53 | 53 |
| 牛顿迭代次数 | 214 | 214 | 214 | 214 | 214 |
| 线性迭代次数 | 5 322 | 5 322 | 5 322 | 5 322 | 5 322 |
| 解法器时间/s | 5 738.62 | 3 125.07 | 1 795.88 | 1 140.44 | 935.73 |
| 并行加速比 | 1.00 | 1.84 | 3.20 | 5.03 | 6.13 |
表1 算例1的并行CPR预条件的数值结果
Table 1 Results of the parallel CPR preconditioner for Example 1
| 解法器 | CPR-FGMRES(30) | ||||
| 线程数 | 1 | 2 | 4 | 8 | 16 |
| 时间步数 | 53 | 53 | 53 | 53 | 53 |
| 牛顿迭代次数 | 214 | 214 | 214 | 214 | 214 |
| 线性迭代次数 | 5 322 | 5 322 | 5 322 | 5 322 | 5 322 |
| 解法器时间/s | 5 738.62 | 3 125.07 | 1 795.88 | 1 140.44 | 935.73 |
| 并行加速比 | 1.00 | 1.84 | 3.20 | 5.03 | 6.13 |
| 解法器 | CPR-FGMRES(30) | ||||
| 线程数 | 1 | 2 | 4 | 8 | 16 |
| 时间步数 | 267 | 267 | 267 | 267 | 267 |
| 牛顿迭代次数 | 1 083 | 1 083 | 1 083 | 1 083 | 1 083 |
| 线性迭代次数 | 16 389 | 16 393 | 16 390 | 16 389 | 16 388 |
| 解法器时间/s | 5 605.10 | 3 067.03 | 1 801.19 | 1 177.64 | 915.39 |
| 并行加速比 | 1.00 | 1.83 | 3.11 | 4.76 | 6.12 |
表2 算例2的并行CPR预条件的数值结果
Table 2 Results of the parallel CPR preconditioner for Example 2
| 解法器 | CPR-FGMRES(30) | ||||
| 线程数 | 1 | 2 | 4 | 8 | 16 |
| 时间步数 | 267 | 267 | 267 | 267 | 267 |
| 牛顿迭代次数 | 1 083 | 1 083 | 1 083 | 1 083 | 1 083 |
| 线性迭代次数 | 16 389 | 16 393 | 16 390 | 16 389 | 16 388 |
| 解法器时间/s | 5 605.10 | 3 067.03 | 1 801.19 | 1 177.64 | 915.39 |
| 并行加速比 | 1.00 | 1.83 | 3.11 | 4.76 | 6.12 |
| 解法器 | CPR-FGMRES(30) | ||||
| 线程数 | 1 | 2 | 4 | 8 | 16 |
| 时间步数 | 147 | 147 | 147 | 147 | 147 |
| 牛顿迭代次数 | 362 | 362 | 362 | 362 | 362 |
| 线性迭代次数 | 3 741 | 3 737 | 3 735 | 3 736 | 3 741 |
| 解法器时间/s | 2 685.36 | 1519.28 | 931.29 | 637.65 | 512.10 |
| 并行加速比 | 1.00 | 1.77 | 2.88 | 4.21 | 5.24 |
表3 算例3的并行CPR预条件的数值结果
Table 3 Results of the parallel CPR preconditioner for Example 3
| 解法器 | CPR-FGMRES(30) | ||||
| 线程数 | 1 | 2 | 4 | 8 | 16 |
| 时间步数 | 147 | 147 | 147 | 147 | 147 |
| 牛顿迭代次数 | 362 | 362 | 362 | 362 | 362 |
| 线性迭代次数 | 3 741 | 3 737 | 3 735 | 3 736 | 3 741 |
| 解法器时间/s | 2 685.36 | 1519.28 | 931.29 | 637.65 | 512.10 |
| 并行加速比 | 1.00 | 1.77 | 2.88 | 4.21 | 5.24 |
| 解法器 | BILU(0)-FGMRES(30) | ||||
| 线程数 | 1 | 2 | 4 | 8 | 16 |
| 时间步数 | 55 | 55 | 55 | 55 | 55 |
| 牛顿迭代次数 | 215 | 215 | 215 | 215 | 215 |
| 线性迭代次数 | 12 198 | 12 384 | 12 313 | 12 143 | 12 189 |
| 解法器时间/s | 14 036.60 | 7 577.14 | 3 989.75 | 2 248.55 | 1 471.24 |
| 并行加速比 | 1.00 | 1.85 | 3.52 | 6.24 | 9.54 |
表4 算例4的并行BILU(0) 预条件的数值结果
Table 4 Results of the parallel BILU(0) preconditioner for Example 4
| 解法器 | BILU(0)-FGMRES(30) | ||||
| 线程数 | 1 | 2 | 4 | 8 | 16 |
| 时间步数 | 55 | 55 | 55 | 55 | 55 |
| 牛顿迭代次数 | 215 | 215 | 215 | 215 | 215 |
| 线性迭代次数 | 12 198 | 12 384 | 12 313 | 12 143 | 12 189 |
| 解法器时间/s | 14 036.60 | 7 577.14 | 3 989.75 | 2 248.55 | 1 471.24 |
| 并行加速比 | 1.00 | 1.85 | 3.52 | 6.24 | 9.54 |
| 解法器 | BAMG-FGMRES(30) | ||||
| 线程数 | 1 | 2 | 4 | 8 | 16 |
| 时间步数 | 55 | 55 | 55 | 55 | 55 |
| 牛顿迭代次数 | 215 | 215 | 215 | 215 | 215 |
| 线性迭代次数 | 2 900 | 2 900 | 2 900 | 2 900 | 2 900 |
| 解法器时间/s | 7 284.81 | 4 307.80 | 2 728.25 | 1 961.85 | 1 658.78 |
| 并行加速比 | 1.00 | 1.69 | 2.67 | 3.71 | 4.39 |
表5 算例4的并行BAMG预条件的数值结果
Table 5 Results of the parallel BAMG preconditioner for Example 4
| 解法器 | BAMG-FGMRES(30) | ||||
| 线程数 | 1 | 2 | 4 | 8 | 16 |
| 时间步数 | 55 | 55 | 55 | 55 | 55 |
| 牛顿迭代次数 | 215 | 215 | 215 | 215 | 215 |
| 线性迭代次数 | 2 900 | 2 900 | 2 900 | 2 900 | 2 900 |
| 解法器时间/s | 7 284.81 | 4 307.80 | 2 728.25 | 1 961.85 | 1 658.78 |
| 并行加速比 | 1.00 | 1.69 | 2.67 | 3.71 | 4.39 |
| 解法器 | CPTR-FGMRES(30) | ||||
| 线程数 | 1 | 2 | 4 | 8 | 16 |
| 时间步数 | 55 | 55 | 55 | 55 | 55 |
| 牛顿迭代次数 | 215 | 215 | 215 | 215 | 215 |
| 线性迭代次数 | 3 676 | 3 676 | 3 676 | 3 676 | 3 676 |
| 解法器时间/s | 5 491.50 | 3 097.00 | 1 809.18 | 1 204.83 | 984.68 |
| 并行加速比 | 1.00 | 1.77 | 3.04 | 4.56 | 5.58 |
表6 算例4的并行CPTR预条件的数值结果
Table 6 Results of the parallel CPTR preconditioner for Example 4
| 解法器 | CPTR-FGMRES(30) | ||||
| 线程数 | 1 | 2 | 4 | 8 | 16 |
| 时间步数 | 55 | 55 | 55 | 55 | 55 |
| 牛顿迭代次数 | 215 | 215 | 215 | 215 | 215 |
| 线性迭代次数 | 3 676 | 3 676 | 3 676 | 3 676 | 3 676 |
| 解法器时间/s | 5 491.50 | 3 097.00 | 1 809.18 | 1 204.83 | 984.68 |
| 并行加速比 | 1.00 | 1.77 | 3.04 | 4.56 | 5.58 |
| 1 |
BEAR J .Dynamics of fluids in porous media[J].Soil Science,1975,120(2):162-163.
DOI |
| 2 |
袁益让.计算石油地质等领域的一些新进展[J].计算物理,2003,20(4):283-290.
DOI |
| 3 |
程林松, 肖双爱.稠油油藏蒸汽-泡沫驱油数值模拟方法[J].计算物理,2003,20(5):463-466.
DOI |
| 4 | AZIZ K , SETTARI A .Petroleum reservoir simulation[M].London: Applied Science Publishers,1979. |
| 5 | CHEN Zhangxin , HUAN Guanren , MA Yuanle .Computational methods for multiphase flows in porous media[M].Philadelphia: Society for Industrial and Applied Mathematics,2006. |
| 6 | ABOU-KASSEM J H , ISLAM M R , ALI S M F .Petroleum reservoir simulation[M].2nd edAmsterdam: Gulf Professional Publishing,2020. |
| 7 | DOGRU A H, FUNG L S K, MIDDYA U, et al. A next-generation parallel reservoir simulator for giant reservoirs[C]//SPE Reservoir Simulation Symposium. The Woodlands, Texas: SPE, 2009: SPE-119272-MS. |
| 8 | WANG H F .Theory of linear poroelasticity with applications to geomechanics and hydrogeology[M].Princeton: Princeton University Press,2000. |
| 9 |
DOUGLAS J Jr , PEACEMAN D W , RACHFORD H H Jr , et al.A method for calculating multi-dimensional immiscible displacement[J].Transactions of the AIME,1959,216(1):297-308.
DOI |
| 10 | DARCY H .Les fontaines publiques de la ville de Dijon[M].Paris: Dalmont,1856. |
| 11 |
叶继根, 吴向红.油气藏三维三相组分模型软件研制与应用[J].计算物理,2000,17(5):548-552.
DOI |
| 12 |
PENG D , ROBINSON D B .A rigorous method for predicting the critical properties of multicomponent systems from an equation of state[J].AIChE Journal,1977,23(2):137-144.
DOI |
| 13 | QIAO Changhe. General purpose compositional simulation for multiphase reactive flow with a fast linear solver[D]. Pennsylvania: Pennsylvania State University, 2015. |
| 14 |
BIOT M A .General theory of three-dimensional consolidation[J].Journal of Applied Physics,1941,12(2):155-164.
DOI |
| 15 |
BIOT M A .Theory of elasticity and consolidation for a porous anisotropic solid[J].Journal of Applied Physics,1955,26(2):182-185.
DOI |
| 16 | 张晨松.油藏数值模拟中的线性解法器[J].数值计算与计算机应用,2022,43(1):1-26. |
| 17 |
BEHIE A , VINSOME P K W .Block iterative methods for fully implicit reservoir simulation[J].Society of Petroleum Engineers Journal,1982,22(5):658-668.
DOI |
| 18 |
BEHIE G A , FORSYTH P A Jr .Incomplete factorization methods for fully implicit simulation of enhanced oil recovery[J].SIAM Journal on Scientific and Statistical Computing,1984,5(3):543-561.
DOI |
| 19 |
CHOW E , PATEL A .Fine-grained parallel incomplete LU factorization[J].SIAM Journal on Scientific Computing,2015,37(2):C169-C193.
DOI |
| 20 | BRANDT A, MCCORMICK S F, RUGE J. Algebraic multigrid (AMG) for automatic multigrid solution with application to geodetic computations[R]. Fort Collins: Institute for Computational Studies, 1983. |
| 21 | STVBEN K, CLEES T, KLIE H, et al. Algebraic multigrid methods (AMG) for the efficient solution of fully implicit formulations in reservoir simulation[C]//SPE Reservoir Simulation Symposium. Houston, Texas, U.S.A. : SPE, 2007: SPE-105832-MS. |
| 22 |
VANěK P , MANDEL J , BREZINA M .Algebraic multigrid by smoothed aggregation for second and fourth order elliptic problems[J].Computing,1996,56(3):179-196.
DOI |
| 23 | WALLIS J R. Incomplete gaussian elimination as a preconditioning for generalized conjugate gradient acceleration[C]//SPE Reservoir Simulation Symposium. San Francisco, California: SPE, 1983: SPE-12265-MS. |
| 24 |
ROY T , JÖNSTHÖVEL T B , LEMON C , et al.A constrained pressure-temperature residual (CPTR) method for non-isothermal multiphase flow in porous media[J].SIAM Journal on Scientific Computing,2020,42(4):B1014-B1040.
DOI |
| 25 | CAI Mingchao , ZHANG Guoping .Comparisons of some iterative algorithms for Biot equations[J].International Journal of Evolution Equations,2015,10(3/4):267-282. |
| 26 | ADLER J H, GASPAR F J, HU Xiaozhe, et al. Robust block preconditioners for Biot's model[C]//International Conference on Domain Decomposition Methods: Domain Decomposition Methods in Science and Engineering XXIV. Svalbard, Norway: Springer, 2018: 3-16. |
| 27 | HONG Qingguo , KRAUS J , LYMBERY M , et al.Parameter-robust convergence analysis of fixed-stress split iterative method for multiple-permeability poroelasticity systems[J].Multiscale Modeling & Simulation,2020,18(2):916-941. |
| 28 |
BERGAMASCHI L , FERRONATO M , GAMBOLATI G .Mixed constraint preconditioners for the iterative solution of FE coupled consolidation equations[J].Journal of Computational Physics,2008,227(23):9885-9897.
DOI |
| 29 | CHRISTIE M A , BLUNT M J .Tenth SPE comparative solution project: A comparison of upscaling techniques[J].SPE Reservoir Evaluation & Engineering,2001,4(4):308-317. |
| 30 |
ODEH A S .Comparison of solutions to a three-dimensional black-oil reservoir simulation problem (includes associated paper 9741)[J].Journal of Petroleum Technology,1981,33(1):13-25.
DOI |
| 31 | KILLOUGH J E, KOSSACK C A. Fifth comparative solution project: evaluation of miscible flood simulators[C]//SPE Symposium on Reservoir Simulation. San Antonio, Texas: SPE, 1987: SPE-16000-MS. |
| 32 | SAAD Y .Iterative methods for sparse linear systems[M].2nd edPhiladelphia: Society for Industrial and Applied Mathematics,2003. |
| 33 | 冯春生. 油藏数值模拟中面向异构体系的多水平法及高效解法器研究[D]. 湘潭: 湘潭大学, 2014. |
| 34 | ZHAO Li , FENG Chunsheng , ZHANG Chensong , et al.Parallel multi-stage preconditioners with adaptive setup for the black oil model[J].Computers & Geosciences,2022,168,105230. |
| 35 |
ZHAO Li , LI Shizhe , ZHANG Chensong , et al.An improved multistage preconditioner on GPUs for compositional reservoir simulation[J].CCF Transactions on High Performance Computing,2023,5(2):144-159.
DOI |
| 36 | ReservoirTeam. OpenCAEPoro: An open-sourse multicomponent multiphase porous media flow simulator[EB/OL]. (2023-02-05)[2023-08-29]. https://github.com/OpenCAEPlus/OpenCAEPoro. |
| 37 | FaspTeam. FASP solver project[EB/OL]. (2023-07-11)[2023-08-29]. https://github.com/FaspDevTeam/faspsolver. |
| [1] | 舒适, 岳孝强, 何剑萌, 徐小文, 莫则尧. 多群辐射扩散问题特征驱动的并行AMG法[J]. 计算物理, 2024, 41(1): 87-97. |
| [2] | 舒适, 黄云清, 阳莺, 蔚喜军, 肖映雄. 一类三维等代数结构面剖分下的代数多重网格算法[J]. 计算物理, 2005, 22(6): 18-22. |
| [3] | 刘朝霞, 常谦顺. 由扩散张量导出的各向异性扩散模型的隐式数值模拟[J]. 计算物理, 2005, 22(4): 365-370. |
| [4] | 李晓峰, 朱本仁. Radon变换在渗流力学反问题中的应用[J]. 计算物理, 2001, 18(2): 115-118. |
| [5] | 付汉清, 常谦顺. 用代数多重网格法求解一维分裂格式的Euler方程[J]. 计算物理, 1997, 14(1): 19-25. |
| [6] | 刘兴平. 非对称线性代数方程组的并行算法[J]. 计算物理, 1994, 11(3): 353-361. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||
版权所有 © 《计算物理》编辑部
地址:北京市海淀区丰豪东路2号 邮编:100094 E-mail:jswl@iapcm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发
