基于残差神经网络的激光转塔气动光学效应快速预测

doi:10.19596/j.cnki.1001-246x.8853

摘要/Abstract

摘要：

采用残差神经网络对来流Ma_∞在0.3~0.8范围内球柱型激光转塔模型的稳态流场开展机器学习, 建立此范围内任意来流条件下的亚声速/跨声速流场预测, 并针对不同视场角下的光束波前畸变评估此模型的预估精度。学习模型可再现转塔流动中的边界层、流动分离以及分离剪切层等流动特征, 尤其包括跨声速流动中的非锚定激波间断现象。基于预测流场计算的不同视场角下的波前分布与根据传统计算流体力学(CFD)模拟流场的结果基本一致。该机器学习方法为工程领域中激光转塔气动光学效应自适应校正提供了策略。

关键词: 激光转塔, 气动光学效应, 跨声速流动, 机器学习, 残差神经网络

Abstract:

The residual neural network is used to carry out machine learning on the steady-state flow field of the hemisphere-on-cylinder laser turret model in the range of Ma=0.3~0.8, and the subsonic/transonic flow field under any incoming flow conditions in this range is established. The prediction accuracy of this model is evaluated for beam wavefront distortion under different view-of-field angles. The learning model reproduces flow characteristics such as boundary layers, flow separation, and separated shear layers in turret flows, including in particular unanchored shock discontinuities in transonic flow. The wavefront distribution based on the predicted flow field under different viewing angles is basically consistent with that calculated based on the flow field of CFD. This machine learning method provides a strategy for adaptive correction of laser turret aero-optical effects in the engineering field.

Key words: laser turret, aero-optic effect, transonic flow, machine learning, residual neural network

陈周纬宇, 任翔, 张飞舟, 谷同祥. 基于残差神经网络的激光转塔气动光学效应快速预测[J]. 计算物理, 2025, 42(2): 160-170.

Zhouweiyu CHEN, Xiang REN, Feizhou ZHANG, Tongxiang GU. Rapid Prediction of Aero-optical Effects of Laser Turret Based on Residual Neural Networks[J]. Chinese Journal of Computational Physics, 2025, 42(2): 160-170.

图/表 12

图1 转塔构型与激光光束出射方向

Fig.1 Turret model and direction of laser beam emission

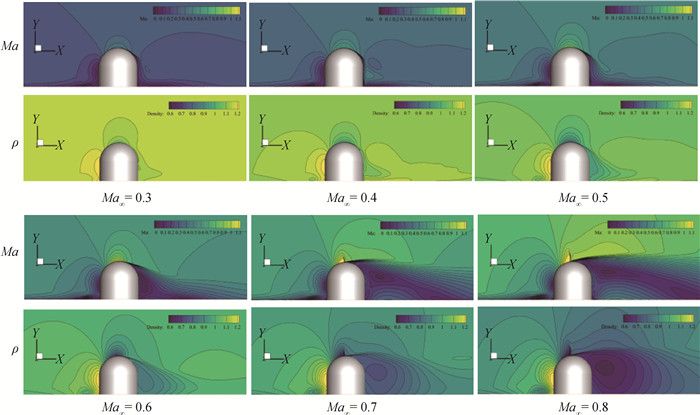
图2 Ma∞=0.3~0.8的部分状态下转塔中心截面上的马赫数和密度分布云图

Fig.2 Mach number and density distribution on center section of turret under partial conditions with Ma∞=0.3~0.8

图3 残差神经网络的结构

Fig.3 Basic structure of residual neural network

表1 三种神经网络的具体参数

Table 1 Parameters of three neural networks

网络	NN-1	NN-2	NN-3
输入	(x, y, z, Ma_∞, ρ_∞)	(x, y, z, Ma_∞, ρ_∞, SDF)	(x, y, z, Ma_∞, ρ_∞, SDF)
网络结构	FC(5, 64)	FC(6, 64)	FC(6, 64)
	ResBlock(32, 64)×4	ResBlock(32, 64)×4	ResBlock(32, 64)×6
	FC(64, 2)
输出	(Ma, ρ)

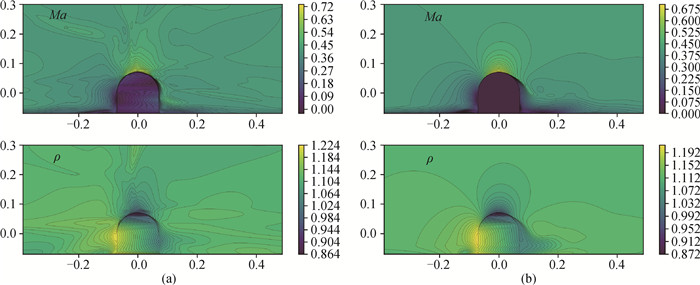
图4 残差神经网络未考虑分场时对来流Ma∞ = 0.42的预测流场和相应CFD的结果(a) 残差网络; (b) CFD

Fig.4 Predicted flow fields for freestream Ma∞=0.42 by residuals neural network without field-specific and CFD (a) residuals neural network; (b) CFD

图5 3种神经网络对CFD的马赫数场的训练结果

Fig.5 Training results of three neural networks on Mach number field of CFD

图6 3种神经网络对CFD的密度场的训练结果

Fig.6 Training results of three neural networks on density field of CFD

图7 3种神经网络预测来流Ma∞=0.42时转塔附近流场分布

Fig.7 Flow field distribution near turret predicted by three neural networks at the freestream flow of Ma∞=0.42

图8 3种神经网络预测来流Ma∞=0.76时转塔附近流场分布

Fig.8 Flow field distribution near turret predicted by three neural networks at the freestream flow of Ma∞=0.76

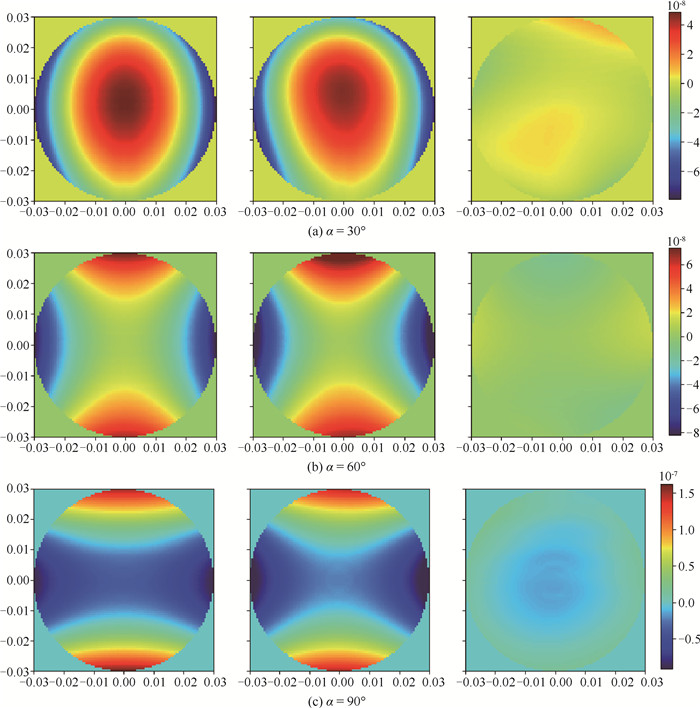
图9 第三种神经网络预测在来流Ma∞=0.42时，视窗角α为(a) 30°、(b) 60°和(c) 90°的波前分布

Fig.9 Wavefront distribution predicted by the third neural network at different α (a) 30°; (b) 60° and (c) 90° with Ma∞=0.42

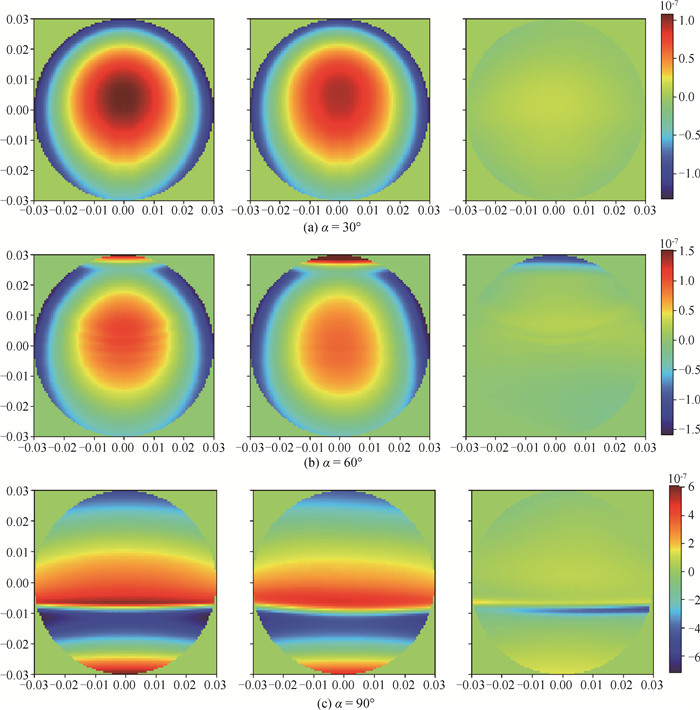
图10 基于第三种神经网络预测在来流Ma∞=0.76时(a)α=30°、(b) 60°和(c) 90°的波前分布

Fig.10 Wavefront distribution of α=30°, 60° and 90° predicted by the third neural networks with freestream flow Ma∞=0.76

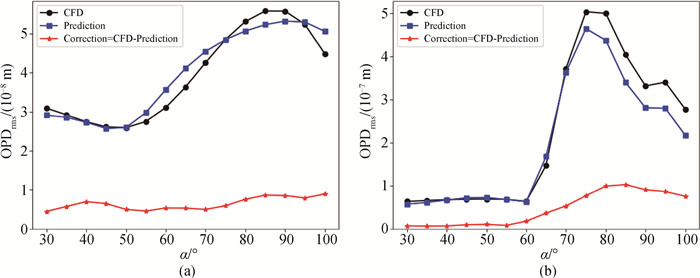
图11 基于第三种神经网络预测的在来流为(a) Ma∞=0.42和(b) Ma∞=0.76时不同视窗角(α=30°~100°) 下波前畸变OPDrms

Fig.11 Wavefront distortion OPDrms predicted by the third neural networks at different viewing window angles (α=30°-100°) with different freestream flows (a) Ma∞=0.42 and (b) Ma∞=0.76

参考文献 34

1	GORDEYEV S , JUMPER E . Fluid dynamics and aero-optics of turrets[J]. Progress in Aerospace Sciences, 2010, 46 (8): 388- 400. DOI
2	WANG Meng , MANI A , GORDEYEV S . Physics and computation of aero-optics[J]. Annual Review of Fluid Mechanics, 2012, 44, 299- 321. DOI
3	JUMPER E J , GORDEYEV S . Physics and measurement of aero-optical effects: Past and present[J]. Annual Review of Fluid Mechanics, 2017, 49 (1): 419- 441. DOI
4	MOLER J L, LAMBERSON S E. Airborne laser (ABL): A legacy and a future for high-energy lasers[C]//Gas and Chemical Lasers and Intense Beam Applications. Bellingham: SPIE, 1998: 99-105.
5	PERRAM G P, MARCINIAK M A, GODA M. High energy laser weapons: Technology overview[C]//Laser Technologies for Defense and Security, Bellingham: SPIE, 2004: 1-25.
6	JUMPER E J , ZENK M , GORDEYEV S , et al. Airborne aero-optics laboratory[J]. Optical Engineering, 2013, 52, 071408. DOI
7	JUMPER E J, GORDEYEV S, CAVALIERI D, et al. Airborne aero-optics laboratory-transonic(AAOL-T)[C]//53rd AIAA Aerospace Sciences Meeting. Kissimmee: American Institute of Aeronautics and Astronautics, 2015: 0675.
8	GORDEYEV S, VOROBIEV A, JUMPER E J, et al. Studies of flow topology around hemisphere at transonic speeds using time-resolved oil flow visualization[C]//54th AIAA Aerospace Sciences Meeting. San Diego: American Institute of Aeronautics and Astronautics, 2016: 1459.
9	NATARAJAN K , KUMAR R . Experimental characterization of supersonic flow over a wall-mounted hemisphere[J]. AIAA Journal, 2021, 59 (11): 4486- 4500. DOI
10	ROEDER A L , GORDEYEV S . Wake response downstream of a spanwise-oscillating hemispherical turret[J]. Journal of Fluids and Structures, 2022, 109, 103470. DOI
11	KIRIAKOS R M , RIVERO M J , KHAMSEH A P , et al. Unsteady motion in the supersonic flow over a wall-mounted hemisphere[J]. AIAA Journal, 2022, 60 (2): 688- 698. DOI
12	POND J E , SUTTON G W . Aero-optic performance of an aircraft forward-facing optical turret[J]. Journal of Aircraft, 2006, 43 (3): 600- 607. DOI
13	LADD J, MANI M, BOWER W. Validation of aerodynamic and optical computations for the unsteady flow field about a hemisphere-on-cylinder turret[C]//27th AIAA Applied Aerodynamics Conference. San Antonio: American Institute of Aeronautics and Astronautics, 2009: 4118.
14	MORGAN P E , VISBAL M R . Hybrid reynolds-averaged Navier-Stokes/large-eddy simulation investigating control of flow over a turret[J]. Journal of Aircraft, 2012, 49 (6): 1700- 1717. DOI
15	JELIC R , SHERER S , GREENDYKE R . Simulation of various turrets at subsonic and transonic flight conditions using OVERFLOW[J]. Journal of Aircraft, 2013, 50 (2): 398- 409. DOI
16	COIRIER W J, WHITELEY M, GOORSKEY D J, et al. Aero-optical evaluation of notional turrets in subsonic, transonic and supersonic regimes[C]//45th AIAA Plasma dynamics and Lasers Conference. Atlanta: American Institute of Aeronautics and Astronautics, 2014: 2355.
17	REN Xiang , YU Huahua , YAO Xianghong , et al. Shock boundary layer interaction and aero-optical effects in a transonic flow over hemisphere-on-cylinder turrets[J]. International Journal of Aerospace Engineering, 2022, 2022, 3397763.
18	LUCCA N D, GORDEYEV S, MORRIDA J J, et al. Modal analysis of the surface pressure field around a hemispherical turret using pressure sensitive paint[C]//2018 AIAA Aerospace Sciences Meeting. Kissimmee: American Institute of Aeronautics and Astronautics, 2018: 0932.
19	SAHBA S , SASHIDHAR D , WILCOX C C , et al. Dynamic mode decomposition for aero-optic wavefront characterization[J]. Optical Engineering, 2022, 61, 013105.
20	WERBOS P J . Backpropagation through time: What it does and how to do it[J]. Proceedings of the IEEE, 1990, 78 (10): 1550- 1560. DOI
21	YNAG Yuting, JIAO Licheng, LIU Xu, et al. Transformers meet visual learning understanding: A comprehensive review[EB/OL]. [2022-03-04]. https://arxiv.org/abs/2203.12944.
22	WONG Manfai , GUO Shangxin , HANG Chingnam , et al. Natural language generation and understanding of big code for AI-Assisted programming: A review[J]. Entropy, 2023, 25 (6): 888. DOI
23	张庆福, 姚军, 黄朝琴, 等. 裂缝性介质多尺度深度学习模型[J]. 计算物理, 2019, 36 (6): 665- 672. DOI
24	郑书昱, 彭佳臻, 张先梅, 等. 基于神经网络的托卡马克能量约束时间预测[J]. 计算物理, 2021, 38 (4): 423- 430. DOI
25	吴国正, 王发杰, 程隋福, 等. 基于物理信息神经网络的内部声场正反问题数值计算[J]. 计算物理, 2022, 39 (6): 687- 698. DOI
26	梁炜光, 桑建兵, 田红艳, 等. 基于数据驱动管道流体湍流模型的系数修正及流动特性分析[J]. 计算物理, 2023, 40 (1): 57- 66. DOI
27	SEKAR V , JIANG Qinghua , SHU Chang , et al. Fast flow field prediction over airfoils using deep learning approach[J]. The Physics of Fluids, 2019, 31 (5): 057103. DOI
28	DURU C , ALEMDAR H , BARAN O U . A deep learning approach for the transonic flow field predictions around airfoils[J]. Computers & Fluids, 2022, 236, 105312.
29	LI Jichao , BOUHLEL M A , MARTINS J R R A . Data-based approach for fast airfoil analysis and optimization[J]. AIAA Journal, 2019, 57 (2): 581- 596. DOI
30	CAI Guobiao , ZHANG Baiyi , LIU Lihui , et al. Fast vacuum plume prediction using a convolutional neural networks-based direct simulation Monte Carlo method[J]. Aerospace Science and Technology, 2022, 129, 107852. DOI
31	LECUN Y , BENGIO Y , HINTON G . Deep learning[J]. Nature, 2015, 521 (7553): 436- 444. DOI
32	GOODEFLLOW I , BENGIO Y , COURVILLE A . Deep learning[M]. Cambridge: MIT Press, 2016.
33	HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas: IEEE, 2016: 770-778.
34	WOLFE W L , ZISSIS G J . The infrared handbook[M]. Arlington: Office of Naval Research, 1978.

[1]	马天星, 郭婷, 黄忠兵, 林海青. 量子蒙特卡罗及其在凝聚态和温稠密物质中的应用[J]. 计算物理, 2024, 41(6): 701-716.
[2]	郭嘉玮, 王涵, 谷同祥. 求解时间发展方程的机器学习方法[J]. 计算物理, 2024, 41(6): 772-782.
[3]	黄灿, 田冷, 王恒力, 王嘉新, 蒋丽丽. 基于条件生成式对抗网络的油藏单井产量预测模型[J]. 计算物理, 2022, 39(4): 465-478.
[4]	潘宏禄, 李俊红, 程晓丽, 马汉东. 气动光学效应湍流脉动模型系数修正[J]. 计算物理, 2018, 35(2): 194-204.
[5]	王光学, 邓小刚, 王运涛, 刘化勇. 三角翼涡破裂的高精度数值模拟[J]. 计算物理, 2012, 29(4): 489-494.
[6]	史可天, 马汉东. 可压缩混合层气动光学效应研究[J]. 计算物理, 2010, 27(1): 65-72.