求解时间发展方程的机器学习方法

doi:10.19596/j.cnki.1001-246x.8987

摘要/Abstract

摘要：

近年来, 使用机器学习方法求解微分方程在不同领域受到越来越多的关注, 然而机器学习方法在求解时间发展方程上遇到许多问题。本文从数据驱动的深度学习方法和基于方程学习的深度学习方法两个方面对现阶段针对时间发展方程的机器学习求解方法进行总结, 并介绍在不同神经网络架构下针对性的求解算法。总结了使用物理信息引入的神经网络方法求解时间发展方程的训练特点与最新工作, 并对未来工作进行展望。

关键词: 神经网络方法, 机器学习方法, 时间发展方程

Abstract:

In recent years, the use of machine learning methods to solve differential equations has attracted increasing attention from researchers in different fields. However, with the deepening of the research, researchers have begun to identify numerous challenges associated with the use of machine learning methods for solving time development equations. This paper presents a summary of the machine learning methods for solving the evolution equation. First, we present a summary of data-driven methods and deep learning methods based on equation learning. Then we introduce targeted algorithms for solving the problem under different neural network architectures. Finally, this paper presents a summary of the training features and recent work on the use of PINN method for solving the evolution equation. It also provides an outlook for future work.

Key words: neural network methods, machine learning methods, evolution equations

郭嘉玮, 王涵, 谷同祥. 求解时间发展方程的机器学习方法[J]. 计算物理, 2024, 41(6): 772-782.

Jiawei GUO, Han WANG, Tongxiang GU. Machine Learning Methods for Solving Evolution Equation[J]. Chinese Journal of Computational Physics, 2024, 41(6): 772-782.

图/表 5

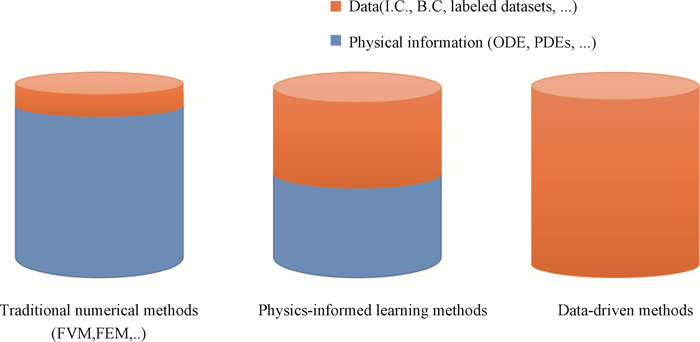
图1 传统数值算法、包含物理信息的学习方法和纯数据驱动方法的数据特征

Fig.1 Data characteristics of traditional numerical methods, physics-informed learning methods and data-driven methods

图2 PINN方法求解时间发展方程示意图

Fig.2 Solution of evolution equations with PINN method

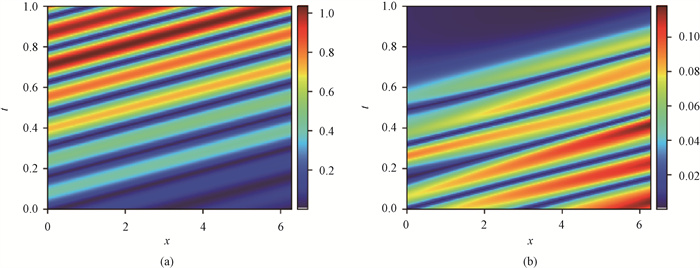
图3 PINN方法求解时间发展方程示意图(Adam优化算法迭代1 500步的训练结果) (a) 逐点误差; (b)逐点残差

Fig.3 Training results of PINN method for solving evolution equation with Adam optimization iteration step of 1 500 (a) point-wise error; (b) point-wise residual

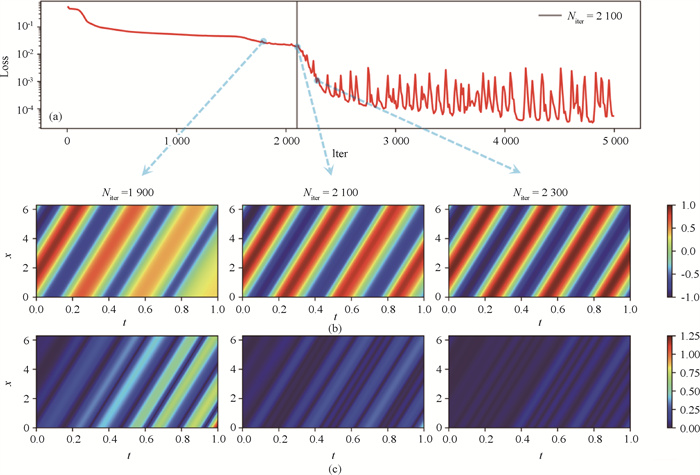
图4 标准PINN方法求解对流方程(2)的训练过程(a)损失函数变化曲线; (b)不同迭代步时神经网络的预测; (c)不同迭代步时神经网络预测的逐点误差

Fig.4 Training process of the standard PINN method for solving convection Eq.(2)(a) loss curves; (b) predictions of neural network at different iteration steps; (c) point-wise errors of neural network predictions at different iteration steps

图5 4种求解时间发展方程PINN方法的时间区间划分方式

Fig.5 Time interval division of four PINN methods for solving the time evolution equation

参考文献 59

1	KRIZHEVSKY A , SUTSKEVER I , HINTON G E . ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60 (6): 84- 90. DOI
2	LI Hang . Deep learning for natural language processing: Advantages and challenges[J]. National Science Review, 2018, 5 (1): 24- 26. DOI
3	LAKE B M , SALAKHUTDINOV R , TENENBAUM J B . Human-level concept learning through probabilistic program induction[J]. Science, 2015, 350 (6266): 1332- 1338. DOI
4	ALIPANAHI B , DELONG A , WEIRAUCH M T , et al. Predicting the sequence specificities of DNA-and RNA-binding proteins by deep learning[J]. Nature Biotechnology, 2015, 33 (8): 831- 838. DOI
5	HORNIK K , STINCHCOMBE M , WHITE H . Multilayer feedforward networks are universal approximators[J]. Neural Networks, 1989, 2 (5): 359- 366. DOI
6	CUOMO S , DI COLA V S , GIAMPAOLO F , et al. Scientific machine learning through physics-informed neural networks: Where we are and what's next[J]. Journal of Scientific Computing, 2022, 92 (3): 88. DOI
7	WANG Sifan , YU Xinling , PERDIKARIS P . When and why PINNs fail to train: A neural tangent kernel perspective[J]. Journal of Computational Physics, 2022, 449, 110768. DOI
8	BISHOP C . Pattern recognition and machine learning(information science and statistics)[M]. Berlin, Heidelberg: Springer, 2006.
9	RAJAN K . Materials informatics[J]. Materials Today, 2005, 8 (10): 38- 45. DOI
10	MONTÁNS F J , CHINESTA F , GÓMEZ B R , et al. Data-driven modeling and learning in science and engineering[J]. Comptes Rendus Mécanique, 2019, 347 (11): 845- 855. DOI
11	BRENEMAN C M , BRINSON L C , SCHADLER L S , et al. Stalking the materials genome: A data-driven approach to the virtual design of nanostructured polymers[J]. Advanced Functional Materials, 2013, 23 (46): 5746- 5752. DOI
12	KALIDINDI S R , NIEZGODA S R , SALEM A A . Microstructure informatics using higher-order statistics and efficient data-mining protocols[J]. JOM, 2011, 63 (4): 34- 41. DOI
13	KALIDINDI S R . Data science and cyberinfrastructure: Critical enablers for accelerated development of hierarchical materials[J]. International Materials Reviews, 2015, 60 (3): 150- 168. DOI
14	GUPTA A , CECEN A , GOYAL S , et al. Structure-property linkages using a data science approach: Application to a non-metallic inclusion/steel composite system[J]. Acta Materialia, 2015, 91, 239- 254. DOI
15	KIRCHDOERFER T , ORTIZ M . Data-driven computational mechanics[J]. Computer Methods in Applied Mechanics and Engineering, 2016, 304, 81- 101. DOI
16	GONZÁLEZ D , CHINESTA F , CUETO E . Thermodynamically consistent data-driven computational mechanics[J]. Continuum Mechanics and Thermodynamics, 2019, 31 (1): 239- 253. DOI
17	BAHMANI B , SUN W . Manifold embedding data-driven mechanics[J]. Journal of the Mechanics and Physics of Solids, 2022, 166, 104927. DOI
18	KOU Jiaqing , LE CLAINCHE S , FERRER E . Data-driven eigensolution analysis based on a spatio-temporal Koopman decomposition, with applications to high-order methods[J]. Journal of Computational Physics, 2022, 449, 110798. DOI
19	KARAPIPERIS K , STAINIER L , ORTIZ M , et al. Data-driven multiscale modeling in mechanics[J]. Journal of the Mechanics and Physics of Solids, 2021, 147, 104239. DOI
20	CARRARA P , DE Lorenzisl , STAINIER L , et al. Data-driven fracture mechanics[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 372, 113390. DOI
21	KIM S , KIM I , LEE J , et al. Knowledge integration into deep learning in dynamical systems: An overview and taxonomy[J]. Journal of Mechanical Science and Technology, 2021, 35, 1331- 1342. DOI
22	BAYDIN A G , PEARLMUTTER B A , RADUL A A , et al. Automatic differentiation in machine learning: A survey[J]. Journal of Machine Learning Research, 2017, 18 (1): 5595- 5637.
23	WEINAN E , YU Bing . The deep Ritz method: A deep learning-based numerical algorithm for solving variational problems[J]. Communications in Mathematics and Statistics, 2018, 6, 1- 12.
24	SIRIGNANO J , SPILIOPOULOS K . DGM: A deep learning algorithm for solving partial differential equations[J]. Journal of Computational Physics, 2018, 375, 1339- 1364. DOI
25	RAISSI M , PERDIKARIS P , KARNIADAKIS G E . Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378, 686- 707. DOI
26	ZANG Yaohua , BAO Gang , YE Xiaojing , et al. Weak adversarial networks for high-dimensional partial differential equations[J]. Journal of Computational Physics, 2020, 411, 109409. DOI
27	BERMAN D , BUCZAK A , CHAVIS J , et al. A survey of deep learning methods for cyber security[J]. Information, 2019, 10 (4): 122. DOI
28	CHEN Hongming , ENGKVIST O , WANG Yinhai , et al. The rise of deep learning in drug discovery[J]. Drug Discovery Today, 2018, 23 (6): 1241- 1250. DOI
29	LIANG Ying , NIU Ruiping , YUE Junhong , et al. A physics-informed recurrent neural network for solving time-dependent partial differential equations[J]. International Journal of Computational Methods, 2023, 20, 2341003.
30	DU Yifan , ZAKI T A . Evolutional deep neural network[J]. Physical Review E, 2021, 104 (4/2): 045303.
31	KAO T, ZHAO J, ZHANG L. pETNNs: Partial evolutionary tensor neural networks for solving time-dependent partial differential equations[DB/OL]. arXiv, 2024: 2403.06084(2024-03-10). https://arxiv.org/abs/2403.06084.
32	QU Jiagang , CAI Weihua , ZHAO Yijun . Learning time-dependent PDEs with a linear and nonlinear separate convolutional neural network[J]. Journal of Computational Physics, 2022, 453, 110928. DOI
33	ZHANG Xuan, HELWIG J, LIN Y, et al. SineNet: Learning temporal dynamics in time-dependent partial differential equations[DB/OL]. The Twelfth International Conference on Learning Representations. Vienna, Austria: ICLR, 2024.
34	SHI Xingjian, CHEN Zhourong, WANG Hao, et al. Convolutional LSTM network: a machine learning approach for precipitation nowcasting[C]//Proceedings of the 28th International Conference on Neural Information Processing Systems-Volume 1. Montreal, Canada: MIT Press, 2015: 802-810.
35	RAO Chengping, SUN Hao, LIU Yang. Hard encoding of physics for learning spatiotemporal dynamics[DB/OL]. arXiv, 2021: 2105.00557(2021-05-02). https://arxiv.org/abs/2105.00557.
36	GOSWAMI S , ANITESCU C , CHAKRABORTY S , et al. Transfer learning enhanced physics informed neural network for phase-field modeling of fracture[J]. Theoretical and Applied Fracture Mechanics, 2020, 106, 102447. DOI
37	LU Lu, JIN Pengzhan, KARNIADAKIS G E. Deeponet: Learning nonlinear operators for identifying differential equations based on the Universal approximation theorem of operators[J]. arXiv, 2019: 03193(2020-04-15) [2024-07-01]. https://arxiv.org/abs/1910.03193 .
38	BHATTACHARYA K, HOSSEINI B, KOVACHK N B, et al. Model reduction and neural networks for parametric PDEs[J]. arXiv, 2020: 03180(2021-01-17). https://arxiv.org/abs/2005.03180.
39	LI Z, KOVACHKI N, AZIZZADENESHELI K, et al. Neural operator: Graph kernel network for partial differential equations[J]. arXiv, 2020: 03485(2020-03-07), https://arxiv.org/abs/2003.03485.
40	CHEN R T Q, RUBANOVA Y, BETTENCOURT J, et al. Neural ordinary differential equations[C]//Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal, Canada: Curran Associates Inc., 2018: 6572-6583.
41	LU Lu , JIN Pengzhan , PANG Guofei , et al. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators[J]. Nature Machine Intelligence, 2021, 3 (3): 218- 229. DOI
42	LI Zongyi, KOVACHKI N, AZIZZADENESHELI K, et al. Fourier neural operator for parametric partial differential equations[DB/OL]. arXiv, 2020: 08895(2020-10-18). https://arxiv.org/abs/2010.08895.
43	GOSWAMI S, BORA A, YU Y, et al. Physics-informed deep neural operator networks[DB/OL]. arXiv, 2022: 05748(2020-07-08). https://arxiv.org/abs/2207.05748.
44	WANG Sifan , PERDIKARIS P . Long-time integration of parametric evolution equations with physics-informed DeepONets[J]. Journal of Computational Physics, 2023, 475, 111855. DOI
45	KRISHNAPRIYAN A, GHOLAMI A, ZHE Shandian, et al. Characterizing possible failure modes in physics-informed neural networks[C]//Advances in Neural Information Processing Systems 34(NeurIPS 2021). Online: NeurIPS, 2021: 26548-26560.
46	PENWARDEN M , JAGTAP A D , ZHE Shandian , et al. A unified scalable framework for causal sweeping strategies for physics-informed neural networks (PINNs) and their temporal decompositions[J]. Journal of Computational Physics, 2023, 493, 112464. DOI
47	KATSIARYNA H, ALEXANDER I. Improved training of Physics-Informed neural networks with model ensembleS[DB/OL]. arXiv, 2022: 05108(2023-01-11). https://arxiv.org/pdf/2204.05108.
48	GUO Jiawei , YAO Yanzhong , WANG Han , et al. Pre-training strategy for solving evolution equations based on physics-informed neural networks[J]. Journal of Computational Physics, 2023, 489, 112258. DOI
49	KINGMA D P, BA J. Adam: A method for stochastic optimization[J]. arXiv, 2014: 6980(2017-01-30). https://arxiv.org/abs/1412.6980.
50	WANG Sifan , SANKARAN S , PERDIKARIS P . Respecting causality for training physics-informed neural networks[J]. Computer Methods in Applied Mechanics and Engineering, 2024, 421, 116813. DOI
51	WANG Sifan , TENF Yujun , PERDIKARIS P . Understanding and mitigating gradient flow pathologies in physics-informed neural networks[J]. SIAM Journal on Scientific Computing, 2021, 43 (5): A3055- A3081. DOI
52	KASHEFI A , MUKERJI T . Physics-informed PointNet: A deep learning solver for steady-state incompressible flows and thermal fields on multiple sets of irregular geometries[J]. Journal of Computational Physics, 2022, 468, 111510. DOI
53	MOSELEY B , MARKHAM A , NISSEN-MEYER T . Finite basis physics-informed neural networks (FBPINNs): a scalable domain decomposition approach for solving differential equations[J]. Advances in Computational Mathematics, 2023, 49 (4): 62. DOI
54	MATTEY R , GHOSH S . A novel sequential method to train physics informed neural networks for Allen Cahn and Cahn Hilliard equations[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 390, 114474. DOI
55	COLBY , WIGHT L , ZHAO J . Solving allen-cahn and cahn-hilliard equations using the adaptive physics informed neural networks[J]. Communications in Computational Physics, 2021, 29 (3): 930- 954. DOI
56	LU Lu , MENG Xuhui , MAO Zhiping , et al. DeepXDE: A deep learning library for solving differential equations[J]. SIAM Review, 2021, 63 (1): 208- 228. DOI
57	MCCLENNY L D , BRAGA-NETO U M . Self-adaptive physics-informed neural networks[J]. Journal of Computational Physics, 2023, 474, 111722. DOI
58	JAGTAP A D , KARNIADAKIS G E . Extended physics-informed neural networks(XPINNs): A generalized space-time domain decomposition based deep learning framework for nonlinear partial differential equations[J]. Communications in Computational Physics, 2020, 28, 2002- 2041. DOI
59	KARNIADAKIS G E , KEVREKIDIS I G , LU Lu , et al. Physics-informed machine learning[J]. Nature Reviews Physics, 2021, 3 (6): 422- 440. DOI