计算物理 ›› 2024, Vol. 41 ›› Issue (5): 547-558.DOI: 10.19596/j.cnki.1001-246x.8855
收稿日期:2023-10-30
出版日期:2024-09-25
发布日期:2024-09-14
作者简介:王昆, 男, 博士, 副教授, 硕士生导师, 从事极端条件下材料力学行为机理、数值建模与模拟研究, E-mail: kwang_hnu@163.com
基金资助:
Kun WANG1( ), Jun CHEN2, Pei WANG2, Wenjun HU3, Zheng ZHONG1
), Jun CHEN2, Pei WANG2, Wenjun HU3, Zheng ZHONG1
Received:2023-10-30
Online:2024-09-25
Published:2024-09-14
摘要:
利用Ginzburg-Landau模型思路推广了传统复振幅扩展晶体相场(APFC)模型的发展思路, 提出一种描述不同晶体结构的简单有效方法, 即快速结构APFC模型。以方形相和矩形相为例, 系统地确定了快速结构APFC模型中与结构相关的模型参数, 并通过数值算例检验了该方法的有效性。特别是在处理矩形相的过程中, 研究发现这种方法不仅可以解决矩形相结构稳定性的问题, 还可以描述矩形相和正交层状相之间的结构相变, 证明了该模型具有描述多结构相变的能力。最后, 通过模拟研究经典的圆形晶粒转动-收缩问题, 检验了该模型对物理规律的准确预测能力, 并揭示了不同晶体对称性对晶粒转动-收缩规律的影响。
中图分类号:
王昆, 陈军, 王裴, 祝文军, 钟正. 基于Ginzburg-Landau方法的快速结构复振幅展开晶体相场模型[J]. 计算物理, 2024, 41(5): 547-558.
Kun WANG, Jun CHEN, Pei WANG, Wenjun HU, Zheng ZHONG. Fast Complex-amplitude Expanded Phase Field Crystal Model for Different Crystals through a Ginzburg-Landau Approach[J]. Chinese Journal of Computational Physics, 2024, 41(5): 547-558.
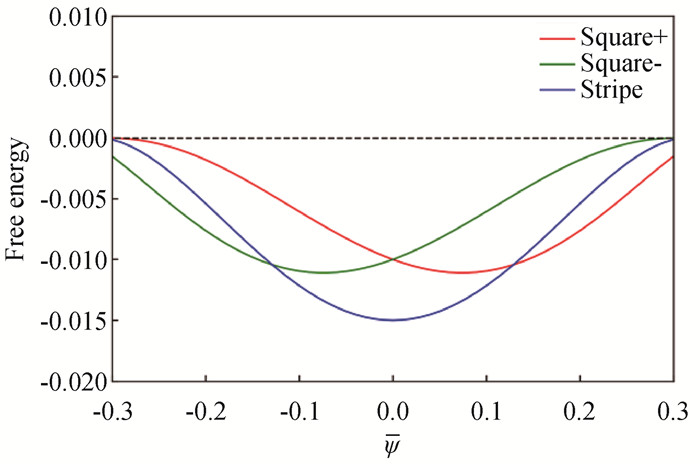
图1 ω4=λ/2,Δfsqmin和Δfstrmin与ψ的函数关系 square+和square-分别对应式(18) 中采用的正负号。
Fig.1 Δfsqmin and Δfstrmin as function of ψ for ω4=λ/2 Square+ and square-correspond to the positive and negative sign adopted in Eq. (18), respectively.

图2 (a) Δfrect和Δfstrmin与ψ的函数关系;(b) (ηⅠ, ηⅡ, ηⅢ)的最优值与ψ的函数关系
Fig.2 (a) Δfrect and Δfstrmin as function of ψ; (b) the optimal solution of (ηⅠ, ηⅡ, ηⅢ) versus ψ
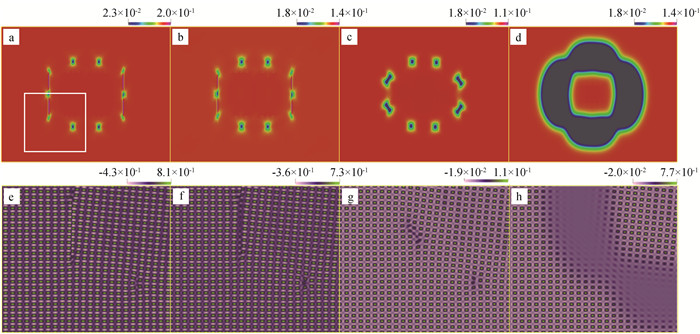
图3 快速APFC模型模拟的完美矩形矩阵中的圆形晶粒嵌入情况(a) ψ=0.1;(b) ψ=0.2;(c) ψ=0.3;(d) ψ=0.4,绘制的场为A2; (e)~(f)是(a)~(d)中同一区域的相应重建原子数密度场,图(a)中的白色实心方框对其进行了特别说明 ε=0.3,g=0,λ=3.0,$\stackrel{◆}{\omega}_4 $=2.1λ,A0=0.2,b=1.25,χani=1.0,κ=0.0。(e)和(f)中的结构显然不同于(g)和(h)中的结构,这是一种新的相,在本文中称为正交分层(OL)相, 在(d)或(h)中,液相开始在晶界处生长。
Fig.3 A circular grain embedding in a otherwise perfect rectangular matrix simulated by the fast APFC model with (a) ψ=0.1; (b) ψ=0.2; (c) ψ=0.3; (d) ψ=0.4, respectively. The field plotted is A2. The figure (e)-(f) is the corresponding reconstructed atom number density field of (a)-(d) from the same region which is specially illustrated in (a) by the white solid square (Other model parameters are ε=0.3, g=0, λ=3.0, $\stackrel{◆}{\omega}_4 $=2.1λ, A0=0.2, b=1.25, χani=1.0 and κ=0.0. The structure in (e) and (f) is apparently different from that of (g) and (h), which is a new phase, referred to as the orthogonal layered (OL) phase in this work. In the figure (d) or (h), the liquid phase begins to grow at the grain boundary.)
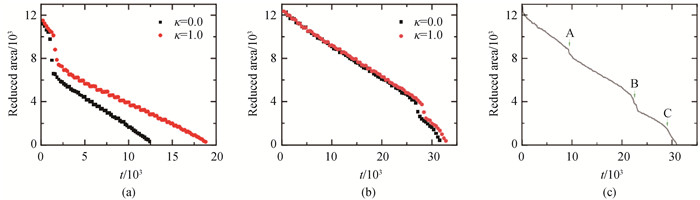
图4 快速APFC模型计算的(a)六角晶格、(b)方形晶格、(c)矩形晶格的圆形晶粒面积与时间的关系(对于矩形晶格,晶粒面积由ra× rb估算,ra (rb)是椭圆晶粒的长(短)轴。对于其他两个晶格,晶粒面积按圆形晶粒半径的平方估算。图(c)中用A、B和C标出了与收缩率变化相对应的三个拐点。)
Fig.4 Area of the circular grain versus time calculated by the fast APFC model for (a) hexagonal lattice; (b) square lattice and (c) rectangular lattice (For the rectangular lattice, the grain area is estimated by ra× rb, ra (rb) is the long (short) axis of the elliptical grain. For the other two lattices, the grain area is estimated by the square of the radius of the circular grain. In (c), the three knees corresponding to the change of the shrinking rate are marked by A, B and C.)
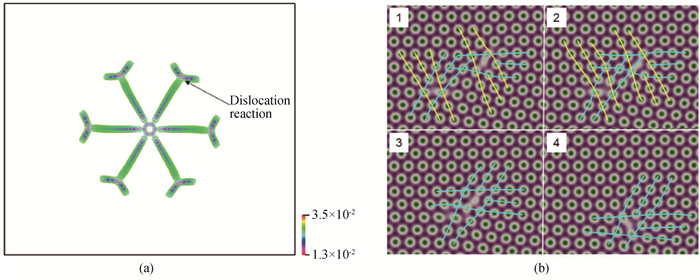
图5 (a) 六角晶中圆形晶粒的位错轨迹,颜色由A2编码;(b)图(a)中箭头所指位置重建的原子数密度演化(图(b)中1~4分别对应于600,800,1 000,1 200时刻,图中黄色和青色线条分别表示具有不同柏氏矢量的混合位错芯。特别地,[${\rm{\bar 1}}$2${\rm{\bar 1}}$0] 位错分量在位错反应后被抵消。)
Fig.5 (a) The trajectory of the dislocations of the circular grain in the hexagonal matrix, where the color is encoded by A2; (b) atom number density evolution reconstructed from the position as pointed by the arrow in the figure (a) ((b) 1-4 correspond to the moment of 600, 800, 1 000 and 1 200, where the mixed dislocation cores with different burgers vectors are depicted by the yellow and cyan lines mark. Specially, the [${\rm{\bar 1}}$2${\rm{\bar 1}}$0] dislocation components depicted by the yellow lines in the figure 1 or 2 of (b) cancel out after the dislocation reaction.)
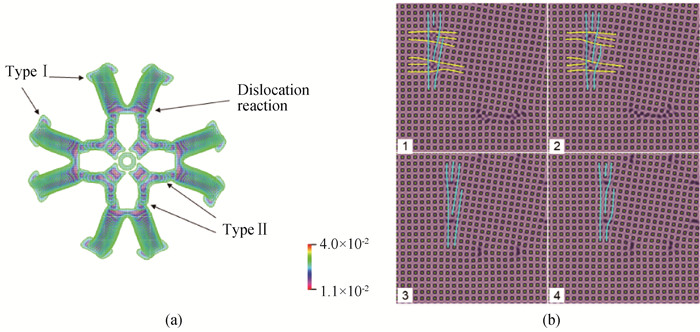
图6 (a) 方形晶中圆形晶粒的位错运动轨迹,其中颜色由A2编码;(b)图(a)中箭头所指位置重建的原子数密度演化(图(b)中1~4分别对应于260 000,268 000,272 000,276 000时刻,黄色和青色线条分别表示不同柏氏矢量的位错芯。特别地,图(b)中1和2中黄线所示的符号相反的<01>位错分量在位错反应后抵消。)
Fig.6 (a) The trajectory of the dislocations of the circular grain in the square matrix, where the color is encoded by A2; (b) Atom number density evolution reconstructed from the position as pointed by the arrow in the figure (a)((b) 1-4 correspond to the moment of 260 000, 268 000, 272 000 and 276 000, where the dislocation cores with different burgers vectors are depicted by the yellow and cyan lines mark. Specially, the <01> dislocation components with the opposite sign depicted by the yellow lines in 1 and 2 of (b) cancel out after the dislocation reaction.)
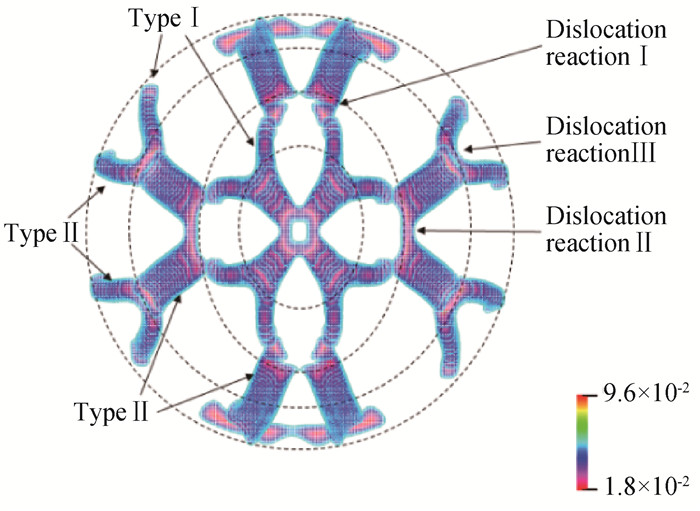
图7 矩形晶中圆形晶粒的位错轨迹和形状(颜色由A2编码同一虚线圆上的位错芯对应同一时刻。)
Fig.7 The trajectory and shape of the dislocations of the circular grain in the rectangular matrix (Where the color is encoded by A2.Dislocation cores on the same dashed circle corresponds to the same moment.)
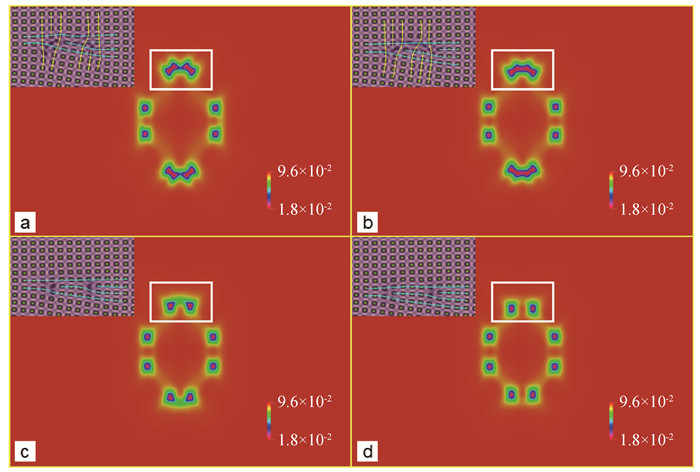
图8 位错反应Ⅱ的A2场,图(a)~(d)分别对应无量纲时间22 400,22 800,23 000,23 200 插图表示从白色实线方框标记的区域重建的原子数密度。黄色和青色线分别表示<10>和<01>位错。
Fig.8 (a) A2 field of dislocation reaction Ⅱ, figure (a)-(d) correspond to the moment of 22 400, 22 800, 2 3000 and 23 200, respectively (The inset shows the reconstructed atom number density from the region marked by the white solid square. The yellow and cyan lines depict the <10> and <01> dislocation, respectively.)
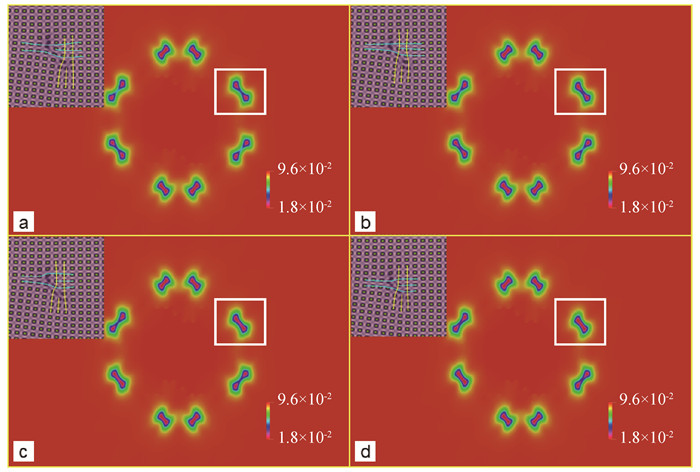
图9 位错反应Ⅲ的A2场,图(a)~(d)分别对应无量纲时间8 000,8 300,8 500,8 700(图中标记的含义与图 8相同。)
Fig.9 A2 field of dislocation reaction Ⅲ, figure (a)-(d) correspond to the moment of 8 000, 8 300, 8 500 and 8 700, respectively (Other conventions are the same as that of Fig. 8.)
| 1 |
ELDER K R , KATAKOWSKI M , HAATAJA M , et al. Modeling elasticity in crystal growth[J]. Physical Review Letters, 2002, 88 (24): 245701.
DOI |
| 2 | ATHREYA B P , GOLDENFELD N , DANTZIG J A . Renormalization-group theory for the phase-field crystal equation[J]. Physical Review E, 2006, 74 (1): 011601. |
| 3 | GOLDENFELD N , ATHREYA B P , DANTZIG J A . Renormalization group approach to multiscale simulation of polycrystalline materials using the phase field crystal model[J]. Physical Review, 2005, 72 (2): 020601. |
| 4 |
ELDER K R , PROVATAS N , BERRY J , et al. Phase-field crystal modeling and classical density functional theory of freezing[J]. Physical Review B, 2007, 75 (6): 064107.
DOI |
| 5 |
SKAUGEN A , ANGHELUTA L , VINALS J . Dislocation dynamics and crystal plasticity in the phase-field crystal model[J]. Physical Review B, 2018, 97 (5): 054113.
DOI |
| 6 |
SALVALAGLIO M , VOIGT A , ELDER K R . Closing the gap between atomic-scale lattice deformations and continuum elasticity[J]. Npj Computational Materials, 2019, 5, 48.
DOI |
| 7 |
AINSWORTH M , MAO Zhiping . Phase field crystal based prediction of temperature and density dependence of elastic constants through a structural phase transition[J]. Physical Review B, 2019, 100 (10): 104101.
DOI |
| 8 |
SALVALAGLIO M , BACKOFEN R , ELDER K R , et al. Defects at grain boundaries: A coarse-grained, three-dimensional description by the amplitude expansion of the phase-field crystal model[J]. Physical Review Materials, 2018, 2 (5): 053804.
DOI |
| 9 | SALVALAGLIO M , BACKOFEN R , VOIGT A , et al. Controlling the energy of defects and interfaces in the amplitude expansion of the phase-field crystal model[J]. Physical Review E, 2017, 96 (2/1): 023301. |
| 10 |
YAMANAKA A , MCREYNOLDS K , VOORHEES P W . Phase field crystal simulation of grain boundary motion, grain rotation and dislocation reactions in a BCC bicrystal[J]. Acta Materialia, 2017, 133, 160- 171.
DOI |
| 11 |
TARP J M , ANGHELUTA L , MATHIESEN J , et al. Intermittent dislocation density fluctuations in crystal plasticity from a phase-field crystal model[J]. Physical Review Letters, 2014, 113 (26): 265503.
DOI |
| 12 |
CHAN P Y , TSEKENIS G , DANTZIG J , et al. Plasticity and dislocation dynamics in a phase field crystal model[J]. Physical Review Letters, 2010, 105 (1): 015502.
DOI |
| 13 |
HU Nengwen , HUANG Yongfeng , WANG Kun , et al. Roles of triple and quadruple junctions on plasticity by phase-field crystal approach[J]. Physica B: Condensed Matter, 2022, 626, 413449.
DOI |
| 14 |
ZHOU Wenquan , WANG Jincheng , LIN Bo , et al. Yielding and jerky plasticity of tilt grain boundaries in high-temperature graphene[J]. Carbon, 2019, 153, 242- 256.
DOI |
| 15 |
GAO Yingjun , DENG Qianqian , QUAN Silong , et al. Phase field crystal simulation of grain boundary movement and dislocation reaction[J]. Frontiers of Materials Science, 2014, 8 (2): 176- 184.
DOI |
| 16 |
HIROUCHI T , TAKAKI T , TOMITA Y . Effects of temperature and grain size on phase-field-crystal deformation simulation[J]. International Journal of Mechanical Sciences, 2010, 52 (2): 309- 319.
DOI |
| 17 |
STEFANOVIC P , HAATAJA M , PROVATAS N . Phase field crystal study of deformation and plasticity in nanocrystalline materials[J]. Physical Review. E, 2009, 80 (4): 046107.
DOI |
| 18 |
HIROUCHI T , TAKAKI T , TOMITA Y . Development of numerical scheme for phase field crystal deformation simulation[J]. Computational Materials Science, 2009, 44 (4): 1192- 1197.
DOI |
| 19 |
WANG Kun , ZHANG Fengguo , HE Anmin , et al. Plasticity and phase transition of crystals under continuous deformations by phase field crystal approach[J]. International Journal of Plasticity, 2019, 122, 225- 243.
DOI |
| 20 |
SKOGVOLL V , SKAUGEN A , ANGHELUTA L , et al. Dislocation nucleation in the phase-field crystal model[J]. Physical Review B, 2021, 103 (1): 014107.
DOI |
| 21 |
SKOGVOLL V , ANGHELUTA L , SKAUGEN A , et al. A phase field crystal theory of the kinematics of dislocation lines[J]. Journal of the Mechanics and Physics of Solids, 2022, 166, 104932.
DOI |
| 22 |
WANG Kun , XIAO Shifang , CHEN Jun , et al. Exploring atomic mechanisms of microstructure evolutions in crystals under vacancy super-or undersaturation states by a kinetic amplitude-expanded phase-field-crystal approach[J]. International Journal of Plasticity, 2022, 157, 103386.
DOI |
| 23 |
MKHONTA S K , ELDER K R , HUANG Z F . Exploring the complex world of two-dimensional ordering with three modes[J]. Physical Review Letters, 2013, 111 (3): 035501.
DOI |
| 24 | WU K , PLAPP M , VOORHEES P W . Controlling crystal symmetries in phase-field crystal models[J]. Journal of Physics, 2010, 22 (36): 364102. |
| 25 | WU Kuoan , ADLAND A , KARMA A . Phase-field-crystal model for fcc ordering[J]. Physical Review E, 2010, 81 (6): 061601. |
| 26 |
GREENWOOD M , OFORI-OPOKU N , ROTTLER J , et al. Modeling structural transformations in binary alloys with phase field crystals[J]. Physical Review B, 2011, 84 (6): 064104.
DOI |
| 27 |
GREENWOOD M , PROVATAS N , ROTTLER J . Free energy functionals for efficient phase field crystal modeling of structural phase transformations[J]. Physical Review Letters, 2010, 105 (4): 045702.
DOI |
| 28 |
WU Kuoan , LIN Shangchun , KARMA A . Two-mode Ginzburg-Landau theory of crystalline anisotropy for fcc-liquid interfaces[J]. Physical Review B, 2016, 93 (5): 054114.
DOI |
| 29 |
WU Kuoan , KARMA A . Phase-field crystal modeling of equilibrium bcc-liquid interfaces[J]. Physical Review B, 2007, 76 (18): 184107.
DOI |
| 30 |
WU Kuoan , KARMA A , HOYT J J , et al. Ginzburg-Landau theory of crystalline anisotropy for bcc-liquid interfaces[J]. Physical Review B, 2006, 73 (9): 094101.
DOI |
| 31 |
SHIH W H , WANG Z Q , ZENG X C , et al. Ginzburg-Landau theory for the solid-liquid interface of bcc elements[J]. Physical Review A, 1987, 35 (6): 2611- 2618.
DOI |
| 32 |
TÓTH G I , PROVATAS N . Erratum: Advanced Ginzburg-Landau theory of freezing: A density-functional approach[J]. Physical Review B, 2014, 90 (17): 179901.
DOI |
| 33 |
TÓTH G I , PROVATAS N . Advanced Ginzburg-Landau theory of freezing: A density-functional approach[J]. Physical Review B, 2014, 90 (10): 104101.
DOI |
| 34 |
MAJANIEMI S , PROVATAS N . Deriving surface-energy anisotropy for phenomenological phase-field models of solidification[J]. Physical Review E, 2009, 79 (1): 011607.
DOI |
| 35 |
WU Kuoan , WANG Chinghao , HOYT J J , et al. Ginzburg-Landau theory of the bcc-liquid interface kinetic coefficient[J]. Physical Review B, 2015, 91 (1): 014107.
DOI |
| 36 |
WU Kuoan , VOORHEES P W . Phase field crystal simulations of nanocrystalline grain growth in two dimensions[J]. Acta Materialia, 2012, 60 (1): 407- 419.
DOI |
| 37 |
UPMANYU M , SROLOVITZ D J , LOBKOVSKY A E , et al. Simultaneous grain boundary migration and grain rotation[J]. Acta Materialia, 2006, 54 (7): 1707- 1719.
DOI |
| [1] | 马文婧, 王进, 郭慧, 吕美妮, 张宏泽, 李冬德. 晶体相场法研究金属微互连结构形变过程对界面Kirkendall空洞生长的抑制机理[J]. 计算物理, 2023, 40(4): 416-424. |
| [2] | 李建伟, 项璇, 王景栋, 胡石, 陈铮, 贺元骅. 不同温度和扰动应变作用下纳米微裂纹的晶体相场研究[J]. 计算物理, 2022, 39(6): 717-726. |
| [3] | 李宏明, 李茂生. 晶体塑性有限元方法研究辐照对多晶铜力学性能的影响[J]. 计算物理, 2022, 39(1): 6-16. |
| [4] | 郭怀民, 赵国忠, 姜丽娟. 磁电弹性体中螺型位错与唇口裂纹的相互作用[J]. 计算物理, 2022, 39(1): 33-40. |
| [5] | 郭怀民, 赵国忠. 磁电弹性体中多条位错与Griffith裂纹[J]. 计算物理, 2020, 37(2): 198-204. |
| [6] | 高英俊, 杨瑞琳, 黄礼琳, 刘瑶. 纳观尺度裂纹扩展微观机理的晶体相场法研究[J]. 计算物理, 2017, 34(4): 453-460. |
| [7] | 罗志荣, 高英俊, 毛鸿, 卢成健, 黄世叶. 相场法模拟第二相颗粒对柱状晶形成的影响[J]. 计算物理, 2016, 33(3): 367-373. |
| [8] | 高英俊, 罗志荣, 邓芊芊, 黄礼琳, 林葵. 韧性材料的微裂纹扩展与分叉的晶体相场模拟[J]. 计算物理, 2014, 31(4): 471-478. |
| [9] | 高英俊, 王江帆, 罗志荣, 卢强华, 刘瑶. 晶体相场方法模拟纳米孪晶结构[J]. 计算物理, 2013, 30(4): 577-581. |
| [10] | 庞卫卫, 张广财, 许爱国, 卢果. 面心立方铜晶体中空洞生长与贯通的尺寸效应[J]. 计算物理, 2011, 28(4): 540-546. |
| [11] | 卢果, 方步青, 张广财. 基于连续介质位错理论的位错原子分布构造方法[J]. 计算物理, 2010, 27(2): 195-202. |
| [12] | 王超营, 孟庆元, 李成祥, 钟康游, 杨志伏. Si中30度部分位错弯结运动特性的分子模拟[J]. 计算物理, 2008, 25(4): 488-492. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||
版权所有 © 《计算物理》编辑部
地址:北京市海淀区丰豪东路2号 邮编:100094 E-mail:jswl@iapcm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发
