基于Cahn-Hilliard相场方程的气体动理学格式

doi:10.19596/j.cnki.1001-246x.8862

摘要/Abstract

摘要：

在有限体积的框架下, 构造基于Cahn-Hilliard相场方程的气体动理学格式, 其界面通量由Chapman-Enskog一阶近似确定。进一步证明提出的模型可准确恢复至Cahn-Hilliard方程。通过若干算例对该模型进行测试, 并与相应的格子玻尔兹曼方法进行对比。结果表明, 该模型在界面捕捉方面具有较好的精度和数值稳定性。本文的研究拓展了气体动理学格式在相场理论的应用, 并为两相流体系统的模拟提供了方案。

关键词: 两相系统, 相场模型, 气体动理学格式, Chapman-Enskog展开

Abstract:

The gas kinetic scheme based on Cahn-Hilliard phase field equation with interfacial fluxes determined by the Chapman-Enskog first-order approximation is constructed in the framework of finite volume. It is further demonstrated that the proposed model can be accurately recovered to Cahn-Hilliard equation. The method is tested through several cases and compared with the corresponding lattice Boltzmann method. The results show that the method in this paper has excellent accuracy and numerical stability for interface trapping. The study extends application of the gas-kinetic scheme to phase-field theory and provides a new solution for the simulation of two-phase fluid systems.

Key words: two-phase system, phase field model, Gas-kinetic scheme, Chapman-Enskog expansion

钟豪, 朱炼华, 包进, 郭照立. 基于Cahn-Hilliard相场方程的气体动理学格式[J]. 计算物理, 2025, 42(2): 171-181.

Hao ZHONG, Lianhua ZHU, Jin BAO, Zhaoli GUO. Gas-kinetic Scheme Based on Cahn-Hilliard Phase-field Equation[J]. Chinese Journal of Computational Physics, 2025, 42(2): 171-181.

图/表 19

图1 GKS界面示意图

Fig.1 Interface diagram of GKS

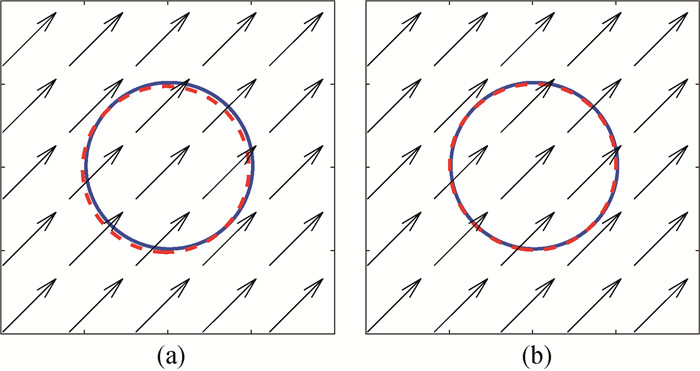
图2 沿对角线平移液滴的相界面形状(Pe=5) (a) LSG-LBM；(b) GKS(实线t=0，虚线t=1T)

Fig.2 Shape of phase interface of diagonally translating droplet (Pe=5) (a) LSG-LBM; (b) GKS (solid line t=0, dashed line t=1T)

图3 沿对角线平移液滴的相界面形状(Pe=5) (a) LSG-LBM; (b) GKS(实线t=0，虚线t=10T)

Fig.3 Shape of phase interface of diagonally translating droplet (Pe=5) (a) LSG-LBM; (b) GKS (solid line t=0, dashed line t=10T)

图4 沿对角线平移液滴的相界面形状(Pe=2 000) (a) LSG-LBM; (b) GKS(实线t=0，虚线t=1T)

Fig.4 Shape of phase interface of diagonally translating droplet (Pe=2 000) (a) LSG-LBM; (b) GKS (solid line t=0, dashed line t=1T)

图5 沿对角线平移液滴的相界面形状(Pe=2 000) (a) LSG-LBM; (b) GKS(实线t=0，虚线t=10T)

Fig.5 Shape of phase interface of diagonally translating droplet (Pe=2 000) (a) LSG-LBM; (b) GKS (solid line t=0, dashed line t=10T)

表1 不同Pe数在1个周期后沿对角线平移液滴的全局误差

Table 1 Global error of translating droplets along the diagonal after 1 period with different Pe numbers

Pe	$ \\|E(\phi)\\|_2$		$\\|E(\phi)\\|_{\max } $
Pe	LSG-LBM	GKS	LSG-LBM	GKS
5	0.112 3	0.036 4	0.611 4	0.223 7
50	0.160 3	0.083 7	0.518 0	0.382 5
500	0.240 2	0.103 5	0.479 6	0.328 0
2 000	0.290 4	0.132 9	0.481 6	0.356 4

图6 GKS和LBM方法L2相对误差随周期数变化

Fig.6 L2 relative error with number of periods for GKS and LBM methods

表2 不同Pe数时1个周期和10个周期后沿对角线平移液滴的质心距离误差

Table 2 Error of center-of-mass distance along diagonal translation of droplet after 1 and 10 periods at different Pe numbers

Pe	t=1T		t=10T
Pe	LSG-LBM	GKS	LSG-LBM	GKS
5	0.75	0.20	4.16	0.94
50	1.01	0.51	3.41	1.54
500	0.83	0.53	2.29	1.31
2 000	0.81	0.51	1.76	1.25

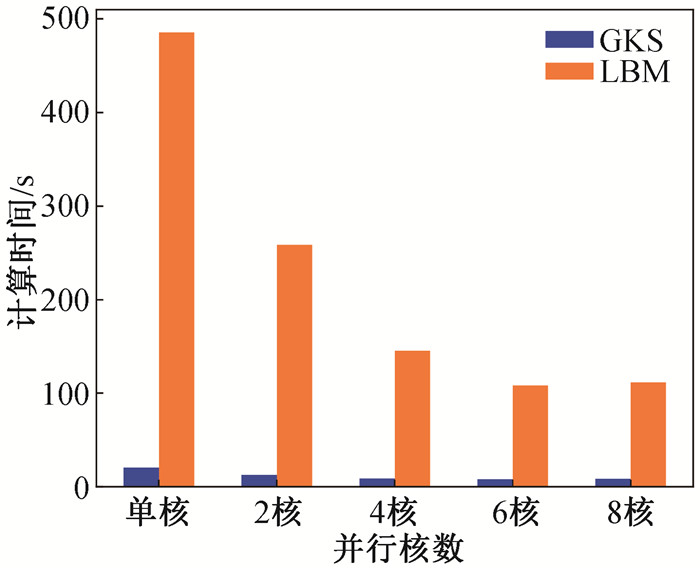
图7 沿对角线平移的液滴GKS和LBM方法的计算时间(Pe=500, n=10)

Fig.7 Computational time between GKS and LBM methods for along diagonal translation of droplet (Pe=500, n=10)

图8 Zalesak圆盘随时间旋转的过程

Fig.8 Rotation of Zalesak disc with time

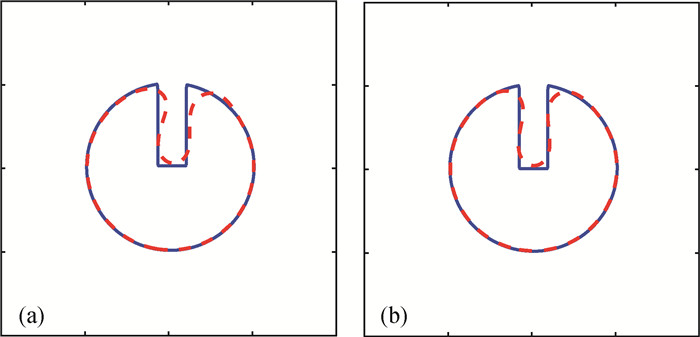
图9 旋转圆盘的相界面形状(Pe=5) (a) LSG-LBM；(b) GKS(实线：t=0，虚线：t=1T)

Fig.9 Shape of the phase interface of rotating disk (Pe=5) (a) LSG-LBM; (b) GKS (solid line t=0, dashed line t=1T)

图10 旋转圆盘的相界面形状(Pe=50) (a) LSG-LBM; (b) GKS(实线t=0，虚线t=1T)

Fig.10 Shape of the phase interface of rotating disk(Pe=50) (a) LSG-LBM; (b) GKS (solid line t=0, dashed line t=1T)

图11 旋转圆盘的相界面形状(Pe=2 000) (a) LSG-LBM; (b) GKS(实线t=0，虚线t=1T)

Fig.11 Shape of the phase interface of rotating disk (Pe=2 000) (a) LSG-LBM; (b) GKS (solid line t=0, dashed line t=1T)

表3 不同Pe数时旋转圆盘的全局误差

Table 3 Global errors of rotating discs at different Pe numbers

Pe	$ \\|E(\phi)\\|_2$		$ \\|E(\phi)\\|_{\max }$
Pe	LSG-LBM	GKS	LSG-LBM	GKS
5	0.072 6	0.055 7	0.978 3	0.972 5
50	0.069 6	0.042 4	0.915 0	0.900 9
500	0.088 0	0.055 8	0.947 5	0.810 5
2 000	1.017 0	0.073 2	4.859 2	0.781 6

图12 单涡剪切流不同时刻的界面重构图(n=2) (a) t=0; (b) t=0.25T; (c) t=0.5T；(d) t=0.75T; (e) t=T

Fig.12 Interface reconfiguration at different moments of single vortex shear flow(n=2) (a) t=0; (b) t=0.25T; (c) t=0.5T; (d) t=0.75T; (e) t=T

图13 单涡剪切流不同时刻的界面重构图(n=4) (a) t=0; (b) t=0.25T; (c) t=0.5T；(d) t=0.75T; (e) t=T

Fig.13 Interface reconfiguration at different moments of single vortex shear flow (n=4) (a) t=0; (b) t=0.25T; (c) t=0.5T; (d) t=0.75T; (e)t=T

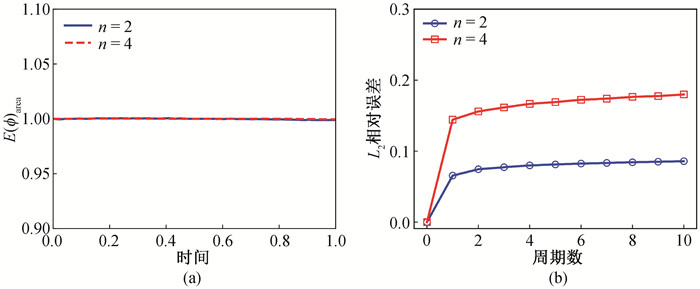
图14 (a) 一个周期内序参量守恒误差随时间的变化；(b) L2相对误差随周期数的变化

Fig.14 (a) Order parameter conservation errors over time in one period; (b) L2 relative error with number of periods

表4 一个周期时单涡剪切流在不同Pe数下的相对误差

Table 4 Relative error of single vortex shear flow at different Pe numbers after one period

Pe	$\\|E(\phi)\\|_2 $
Pe	n=2	n=4
5	0.038 2	0.112 9
50	0.048 3	0.089 6
500	0.065 5	0.144 3
2 000	0.052 9	0.140 2

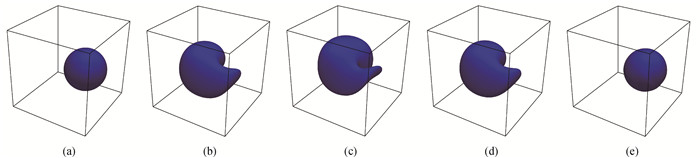
图15 3D单涡剪切流不同时刻的界面重构图(a) t=0; (b) t=0.25T; (c) t=0.5T；(d) t=0.75T; (e) t=T

Fig.15 Interfacial reconfiguration of 3D single-vortex shear flow at different moments of flow (a) t=0; (b) t=0.25T; (c) t=0.5T; (d) t=0.75T; (e) t=T

参考文献 47

1	HYMAN J M . Numerical methods for tracking interfaces[J]. Physica D. Nonlinear Phenomena, 1984, 12 (1/3): 396- 407.
2	王昭, 严红. 基于气液相界面捕捉的统一气体动理学格式[J]. 力学学报, 2018, 50 (4): 711- 721.
3	HIRT C W , NICHOLS B D . Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39 (1): 201- 225. DOI
4	SUSSMAN M , ALMGREN A S , BELL J B , et al. An adaptive level set approach for incompressible Two-Phase flows[J]. Journal of Computational Physics, 1999, 148 (1): 81- 124. DOI
5	ANDERSON D M , MCFADDEN G B , WHEELER A A . Diffuse-Interface methods in fluid mechanics[J]. Annual Review of Fluid Mechanics, 1998, 30, 139- 165. DOI
6	JACQMIN D . Calculation of Two-Phase navier-stokes flows using Phase-Field modeling[J]. Journal of Computational Physics, 1999, 155 (1): 96- 127. DOI
7	ROWLINSON J S . Translation of J. D. van der Waals' "The thermodynamik theory of capillarity under the hypothesis of a continuous variation of density"[J]. Journal of Statistical Physics, 1979, 20 (2): 197- 200. DOI
8	冯其红, 赵蕴昌, 王森, 等. 基于相场方法的孔隙尺度油水两相流体流动模拟[J]. 计算物理, 2020, 37 (4): 439- 447.
9	娄钦, 汤升, 王浩原. 基于格子Boltzmann大密度比模型的多孔介质内气泡动力学行为数值模拟[J]. 计算物理, 2021, 38 (3): 289- 300. DOI
10	SUSSMAN M , SMEREKA P , OSHER S . A level set approach for computing solutions to incompressible two-phase flow[J]. Journal of Computational Physics, 1994, 114 (1): 146- 159. DOI
11	AKHLAGHI AMIRI H A , HAMOUDA A A . Evaluation of level set and phase field methods in modeling two phase flow with viscosity contrast through dual-permeability porous medium[J]. International Journal of Multiphase Flow, 2013, 52, 22- 34. DOI
12	GINGOLD R A , MONAGHAN J J . Smoothed particle hydrodynamics: Theory and application to non-spherical stars[J]. Monthly Notices of the Royal Astronomical Society, 1977, 181 (3): 375- 389. DOI
13	XIONG Qingang , DENG Lijuan , WANG Wei , et al. SPH method for two-fluid modeling of particle-fluid fluidization[J]. Chemical Engineering Science, 2011, 66 (9): 1859- 1865. DOI
14	SHANG Xiaopeng , ZHANG Xuan , NGUYEN T B , et al. Direct numerical simulation of evaporating droplets based on a sharp-interface algebraic VOF approach[J]. International Journal of Heat and Mass Transfer, 2022, 184, 122282. DOI
15	CAHN J W , HILLIARD J E . Free energy of a nonuniform system. Ⅲ. nucleation in a Two-Component incompressible fluid[J]. The Journal of Chemical Physics, 1959, 31 (3): 688- 699. DOI
16	LOWENGRUB J , TRUSKINOVSKY L . Quasi-incompressible Cahn-Hilliard fluids and topological transitions[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1998, 454 (1978): 2617- 2654. DOI
17	HE Xiaoyi , CHEN Shiyi , ZHANG Raoyang . A lattice boltzmann scheme for incompressible multiphase flow and its application in simulation of rayleigh-taylor instability[J]. Journal of Computational Physics, 1999, 152 (2): 642- 663. DOI
18	ZHENG H W , SHU C , CHEW Y T . Lattice boltzmann interface capturing method for incompressible flows[J]. Physical Review. E, Statistical, Nonlinear, and soft Matter Physics, 2005, 72 (5 Pt 2): 056705.
19	ZU Y Q , HE S . Phase-field-based lattice Boltzmann model for incompressible binary fluid systems with density and viscosity contrasts[J]. Physical Review. E, Statistical, Nonlinear, and soft Matter Physics, 2013, 87 (4): 043301. DOI
20	LIANG Hong , XU Jiangrong , CHEN Jiangxing , et al. Phase-field-based lattice Boltzmann modeling of large-density-ratio two-phase flows[J]. Physical Review E, 2018, 97 (3/1): 033309.
21	ZHANG Chunhua , GUO Zhaoli , LI Yibao . A fractional step lattice Boltzmann model for two-phase flow with large density differences[J]. International Journal of Heat and Mass Transfer, 2019, 138, 1128- 1141. DOI
22	INAMURO T , OGATA T , TAJIMA S , et al. A lattice Boltzmann method for incompressible two-phase flows with large density differences[J]. Journal of Computational Physics, 2004, 198 (2): 628- 644. DOI
23	LEE T , LIU Lin . Lattice boltzmann simulations of micron-scale drop impact on dry surfaces[J]. Journal of Computational Physics, 2010, 229 (20): 8045- 8063. DOI
24	李洋, 苏婷, 梁宏, 等. 耦合界面力的两相流相场格子Boltzmann模型[J]. 物理学报, 2018, 67 (22): 224701.
25	FAKHARI A , MITCHELL T , LEONARDI C , et al. Improved locality of the phase-field lattice-Boltzmann model for immiscible fluids at high density ratios[J]. Physical Review E, 2017, 96 (5/1): 053301.
26	SCHWARZMEIER C , HOLZER M , MITCHELL T , et al. Comparison of free-surface and conservative Allen-Cahn phase-field lattice Boltzmann method[J]. Journal of Computational Physics, 2023, 473, 111753. DOI
27	娄钦, 臧晨强, 王浩原, 等. 微通道内不混溶气液两相二氧化碳界面动力学行为的格子Boltzmann研究[J]. 计算物理, 2019, 36 (2): 153- 164. DOI
28	GUO Zhaoli , XU Kun , WANG Ruijie . Discrete unified gas kinetic scheme for all Knudsen number flows: Low-speed isothermal case[J]. Physical Review. E, Statistical, Nonlinear, and soft Matter Physics, 2013, 88 (3): 033305. DOI
29	ZHANG Chunhua , YANG Kang , GUO Zhaoli . A discrete unified gas-kinetic scheme for immiscible two-phase flows[J]. International Journal of Heat and Mass Transfer, 2018, 126 (Part B): 1326- 1336.
30	ZHANG Chunhua , WANG Liangping , LIANG Hong , et al. Central-moment discrete unified gas-kinetic scheme for incompressible two-phase flows with large density ratio[J]. Journal of Computational Physics, 2023, 482, 112040. DOI
31	YANG Zeren , ZHONG Chengwen , ZHUO Congshan . Phase-field method based on discrete unified gas-kinetic scheme for large-density-ratio two-phase flows[J]. Physical Review E, 2019, 99 (4/1): 043302.
32	LIANG H , SHI B C , GUO Z L , et al. Phase-field-based multiple-relaxation-time lattice Boltzmann model for incompressible multiphase flows[J]. Physical Review. E, Statistical, Nonlinear, and soft Matter Physics, 2014, 89 (5): 053320. DOI
33	XU K. Gas-kinetic schemes for unsteady compressible flow simulations[C]//Computational Fluid Dynamics, Annual Lecture Series, 29th, Rhode-Saint-Genese. Belgium, 1998.
34	LI Qibing , FU Song . On the multidimensional gas-kinetic BGK scheme[J]. Journal of Computational Physics, 2006, 220 (1): 532- 548. DOI
35	LI Qibing , XU Kun , FU Song . A high-order gas-kinetic Navier-Stokes flow solver[J]. Journal of Computational Physics, 2010, 229 (19): 6715- 6731. DOI
36	ZHANG Chao , LI Qibing , FU Song , et al. A third-order gas-kinetic CPR method for the Euler and Navier-Stokes equations on triangular meshes[J]. Journal of Computational Physics, 2018, 363, 329- 353. DOI
37	PAN Liang , XU Kun , LI Qibing , et al. An efficient and accurate two-stage fourth-order gas-kinetic scheme for the Euler and NavierStokes equations[J]. Journal of Computational Physics, 2016, 326 (C): 197- 221.
38	XIE Qing , JI Xing , QIU Zihua , et al. High-Order spectral difference gas-kinetic schemes for euler and Navier-Stokes equations[J]. East Asian Journal on Applied Mathematics, 2023, 13 (3): 499- 523. DOI
39	YANG Yaqing , PAN Liang , XU Kun . Implicit high-order gas-kinetic schemes for compressible flows on three-dimensional unstructured meshes Ⅰ: Steady flows[J]. Journal of Computational Physics, 2024, 505, 112902. DOI
40	LI Qibing , FU Song , XU Kun . A compressible Navier-Stokes flow solver with scalar transport[J]. Journal of Computational Physics, 2005, 204 (2): 692- 714. DOI
41	KOLOBOV V I , ARSLANBEKOV R R . Towards adaptive kinetic-fluid simulations of weakly ionized plasmas[J]. Journal of Computational Physics, 2012, 231 (3): 839- 869. DOI
42	ZHAO Wenjin , CAO Guiyu , WANG Jianchun , et al. High-order gas-kinetic schemes with non-compact and compact reconstruction for implicit large eddy simulation[J]. Computers & Fluids, 2023, 256, 105846.
43	XU K . A kinetic method for hyperbolic-elliptic equations and its application in Two-Phase flow[J]. Journal of Computational Physics, 2001, 166 (2): 383- 399. DOI
44	LI Qibing , FU Song . A gas-kinetic BGK scheme for gas-water flow[J]. Computers & Mathematics With Applications, 2011, 61 (12): 3639- 3652.
45	佘邦伟, 赵桂萍. 可压缩非守恒型两相流模型的GKS方法[J]. 计算物理, 2012, 29 (1): 51- 57.
46	WANG Yu , WEN Mengke , LI Weidong . Gas-kinetic scheme based phase-field method for numerical simulations of dendrite growth[J]. Computers & Fluids, 2023, 251, 105737.
47	ZHANG Chunhua , GUO Zhaoli , LIANG Hong . High-order lattice-Boltzmann model for the Cahn-Hilliard equation[J]. Physical Review E, 2019, 99 (4/1): 043310.

[1]	徐云, 龙瑶, 向美珍, 陈军. 非均质炸药的Eshelby夹杂理论相场方法[J]. 计算物理, 2024, 41(5): 559-568.
[2]	魏雪丹, 戴厚平, 李梦军, 郑洲顺. 一维空间Riesz分数阶对流扩散方程的格子Boltzmann方法[J]. 计算物理, 2021, 38(6): 683-692.
[3]	段雅丽, 陈先进, 孔令华. Burgers-Korteweg-de Vries复合方程的格子Boltzmann方法模拟[J]. 计算物理, 2015, 32(6): 639-648.