计算物理 ›› 2022, Vol. 39 ›› Issue (6): 717-726.DOI: 10.19596/j.cnki.1001-246x.8509
李建伟1( ), 项璇1, 王景栋1, 胡石1, 陈铮2, 贺元骅1,*(
), 项璇1, 王景栋1, 胡石1, 陈铮2, 贺元骅1,*( )
)
收稿日期:2022-01-17
出版日期:2022-11-25
发布日期:2023-04-01
通讯作者:
贺元骅
作者简介:李建伟(1995-),男,硕士生,主要从事计算物理研究,E-mail: lijianwei5566@126.com
Jianwei LI1( ), Xuan XIANG1, Jingdong WANG1, Shi HU1, Zheng CHEN2, Yuanhua HE1,*(
), Xuan XIANG1, Jingdong WANG1, Shi HU1, Zheng CHEN2, Yuanhua HE1,*( )
)
Received:2022-01-17
Online:2022-11-25
Published:2023-04-01
Contact:
Yuanhua HE
摘要:
用晶体相场模型模拟扰动应变下纳米微裂纹的扩展行为,探讨扰动频率及温度对微裂纹扩展行为及稳定性的影响。结果表明: 温度提升在扰动频率较小时能引起脆韧转变,裂纹稳定性因温度升高而下降。扰动频率的提升在温度低于脆韧转变温度时,能在演化初期引起脆韧转变,之后将抑制脆性扩展,但无法引起韧脆转变;当温度高于脆韧转变温度时,扰动频率不再改变裂纹扩展模式。裂纹稳定性随扰动频率的增大先下降后上升。
李建伟, 项璇, 王景栋, 胡石, 陈铮, 贺元骅. 不同温度和扰动应变作用下纳米微裂纹的晶体相场研究[J]. 计算物理, 2022, 39(6): 717-726.
Jianwei LI, Xuan XIANG, Jingdong WANG, Shi HU, Zheng CHEN, Yuanhua HE. Propagation of Nanoscale Microcrack Under Disturbance Strain at Different Temperatures: Phase-Field-Crystal Model[J]. Chinese Journal of Computational Physics, 2022, 39(6): 717-726.
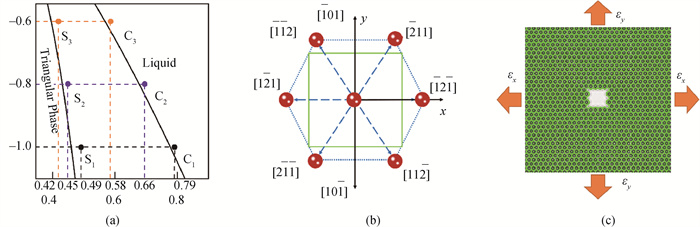
图1 (a) 单模晶体相场二维相图;(b)初始裂纹与三角晶格点阵之间的取向关系示意图(蓝色六边形框表示三角晶格,绿色方框表示初始裂纹。为便于对比,对两者尺寸进行了相对调整。);(c) 初始模拟体系(绿色区域表示三角晶格固相区,白色区域表示中心裂纹。)
Fig.1 (a) Two-dimensional phase diagram calculated with one-mode approximation; (b) A schematic of the orientation between the crack and the lattice (The blue hexagon box signifies the triangular lattice. The green square box indicates the crack. The dimensions are relatively adjusted to facilitate analysis.); (c) illustration of the initial simulation system(Green and white regions indicate triangular lattice and central crack, respectively.)
| 体系 | 温度r | 频率ω /(10-5Δt-1) | 体系 | 温度r | 频率ω /(10-5Δt-1) | 体系 | 温度r | 频率ω /(10-5Δt-1) | ||
| A1 | -1.0 | 无扰动 | A2 | -0.8 | 无扰动 | A3 | -0.6 | 无扰动 | ||
| B1 | -1.0 | 0.2 | B2 | -0.8 | 0.2 | B3 | -0.6 | 0.2 | ||
| C1 | -1.0 | 2 | C2 | -0.8 | 2 | C3 | -0.6 | 2 | ||
| D1 | -1.0 | 20 | D2 | -0.8 | 20 | D3 | -0.6 | 20 | ||
| E1 | -1.0 | 200 | E2 | -0.8 | 200 | E3 | -0.6 | 200 | ||
| F1 | -1.0 | 2 000 | F2 | -0.8 | 2 000 | F3 | -0.6 | 2 000 |
表1 模拟体系及选用参数
Table 1 Parameters of the simulation systems
| 体系 | 温度r | 频率ω /(10-5Δt-1) | 体系 | 温度r | 频率ω /(10-5Δt-1) | 体系 | 温度r | 频率ω /(10-5Δt-1) | ||
| A1 | -1.0 | 无扰动 | A2 | -0.8 | 无扰动 | A3 | -0.6 | 无扰动 | ||
| B1 | -1.0 | 0.2 | B2 | -0.8 | 0.2 | B3 | -0.6 | 0.2 | ||
| C1 | -1.0 | 2 | C2 | -0.8 | 2 | C3 | -0.6 | 2 | ||
| D1 | -1.0 | 20 | D2 | -0.8 | 20 | D3 | -0.6 | 20 | ||
| E1 | -1.0 | 200 | E2 | -0.8 | 200 | E3 | -0.6 | 200 | ||
| F1 | -1.0 | 2 000 | F2 | -0.8 | 2 000 | F3 | -0.6 | 2 000 |
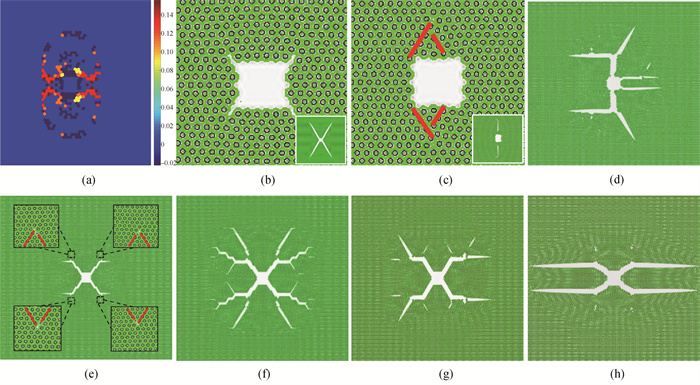
图2 (a) 体系A1在n = 27 000时的应变分布;(b) 体系A1在n = 27 000时的形貌,白色方框区域为体系在n = 60 000时的形貌;(c) 体系C1在n = 13 000时的形貌,白色方框区域为体系在n = 40 000时的中心裂纹的局部形貌,红色线段指示刃位错的多余原子面;(d) 体系C1在n = 57 000时的形貌;(e) 体系D1在n = 45 000时的裂纹形貌;(f) 体系D1在n = 60 000时的形貌;(g) 体系E1在n = 60 000时的形貌;(h) 体系F1在n = 67 000时的形貌
Fig.2 (a) Strain distribution pattern of system A1 at n = 27 000; (b) Morphology of system A1 at n = 27 000 (The inset is a local morphology around the central crack at n = 60 000.); (c) Morphology of system C1 at n = 13 000 (The inset is a local morphology around the central crack at n = 40 000.); (d) Morphology of system C1 at n = 57 000; (e) Morphology of system D1 at n = 45 000; (f) Morphology of system D1 at n = 60 000; (g) Morphology of system E1 at n = 60 000; (h) Morphology of system F1 at n = 67 000 (The extra half planes of atoms are indicated by the red lines.)
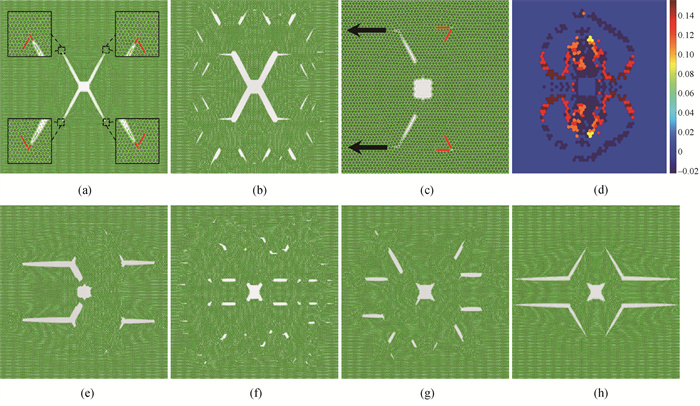
图3 (a) 体系B2在n = 38 000时的形貌,其中红色线段指示刃位错的多余原子面;(b) 体系B2在n = 55 000时的形貌;(c) 体系C2在n = 30 000时的形貌,黑色箭头指示裂纹尖端扩展方向;(d) 体系C2在n = 18 000时的应变分布;(e) 体系C2在n = 57 000时的形貌;(f) 体系D2在n = 60 000时的形貌;(g) 体系E2在n = 60 000时的形貌;(h) 体系F2在n = 60 000时的形貌
Fig.3 (a) Morphology of system B2 at n = 38 000 (The red lines indicate extra half planes of atoms.); (b) Morphology of system B2 at n = 55 000; (c) Morphology of system C2 at n = 30 000 (The black arrows indicate crack propagation direction.); (d) Strain distribution pattern of system C2 at n = 18 000; (e) Morphology of system C2 at n = 57 000; (f) Morphology of system D2 at n = 60 000; (g) Morphology of system E2 at n = 60 000; (h) Morphology of system F2 at n = 60 000

图4 (a) 体系A3在n = 50 000时的形貌;(b) 体系B3在n = 43 000时的形貌;(c) 体系C3在n = 49 000时的形貌;(d) 体系D3在n = 51 000时的形貌;(e) 体系E3在n = 50 000时的形貌;(f) 体系F3在n = 51 000时的形貌
Fig.4 (a) Morphology of system A3 at n = 50 000; (b) Morphology of system B3 at n = 43 000; (c) Morphology of system C3 at n = 49 000; (d) Morphology of system D3 at n = 51 000; (e) Morphology of system E3 at n = 50 000; (f) Morphology of system F3 at n = 51 000
| 体系 | 裂纹扩展模式 | 体系 | 裂纹扩展模式 | 体系 | 裂纹扩展模式 | ||
| A1 | 脆性扩展 | A2 | 脆性扩展 | A3 | 韧性扩展 | ||
| B1 | 脆性扩展 | B2 | 韧性扩展 | B3 | 韧性扩展 | ||
| C1 | 韧性扩展 | C2 | 韧性扩展 | C3 | 韧性扩展 | ||
| D1 | 韧性扩展 | D2 | 韧性扩展 | D3 | 韧性扩展 | ||
| E1 | 韧性扩展 | E2 | 韧性扩展 | E3 | 韧性扩展 | ||
| F1 | 韧性扩展 | F2 | 韧性扩展 | F3 | 韧性扩展 |
表2 各模拟体系的裂纹扩展模式
Table 2 Crack propagation modes of simulated systems
| 体系 | 裂纹扩展模式 | 体系 | 裂纹扩展模式 | 体系 | 裂纹扩展模式 | ||
| A1 | 脆性扩展 | A2 | 脆性扩展 | A3 | 韧性扩展 | ||
| B1 | 脆性扩展 | B2 | 韧性扩展 | B3 | 韧性扩展 | ||
| C1 | 韧性扩展 | C2 | 韧性扩展 | C3 | 韧性扩展 | ||
| D1 | 韧性扩展 | D2 | 韧性扩展 | D3 | 韧性扩展 | ||
| E1 | 韧性扩展 | E2 | 韧性扩展 | E3 | 韧性扩展 | ||
| F1 | 韧性扩展 | F2 | 韧性扩展 | F3 | 韧性扩展 |
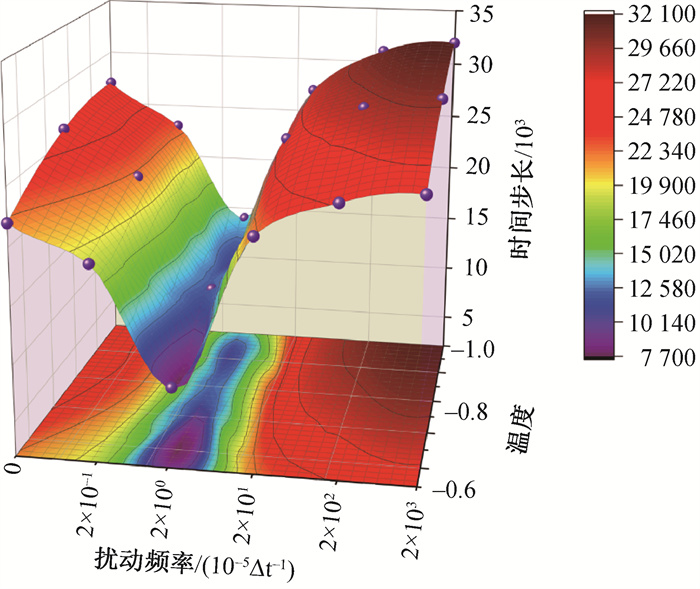
图5 不同扰动频率及体系温度下中心裂纹失稳开始时间步长
Fig.5 Time step number at which the central crack beginning to lose stability under different disturbance frequencies and system temperatures
| 1 |
DOI |
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
DOI |
| 7 |
|
| 8 |
陈成, 陈铮, 杨涛, 等. 晶体相场模型的研究进展[J]. 材料导报, 2012, 26 (9): 116- 119. 116-119, 141
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
吴璐, 潘荣剑, 张伟, 等. 双模晶体相场研究六方四方相变过程晶界和位错演化[J]. 稀有金属材料与工程, 2020, 49 (12): 4103- 4111.
|
| 14 |
DOI |
| 15 |
DOI |
| 16 |
DOI |
| 17 |
赵宇龙, 陈铮, 龙建, 等. 晶体相场法模拟纳米晶材料反霍尔-佩奇效应的微观变形机理[J]. 物理学报, 2013, 62 (11): 118102.
|
| 18 |
马文婧, 柯常波, 周敏波, 等. Sn/Cu互连体系界面和金属间化合物层Kirkendall空洞演化和生长动力学的晶体相场法模拟[J]. 金属学报, 2015, 51 (7): 873- 882.
|
| 19 |
DOI |
| 20 |
卢艳丽, 卢广明, 胡婷婷, 等. 晶体相场法研究Kirkendall效应诱发的相界空洞的形成和演变[J]. 金属学报, 2015, 51 (7): 866- 872.
|
| 21 |
|
| 22 |
郭刘洋, 陈铮, 龙建, 等. 晶体相场法研究应力状态及晶体取向对微裂纹尖端扩展行为的影响[J]. 物理学报, 2015, 64 (17): 178102.
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| [1] | 李洪, 章立新, 任燕, 高明, 刘婧楠. 基于灰色关联分析的BP神经网络对混流闭式冷却塔出水温度的预测[J]. 计算物理, 2022, 39(1): 53-59. |
| [2] | 杨展康, 牛奕. 温度及围护通风对独头巷道氡浓度分布的影响[J]. 计算物理, 2021, 38(4): 456-464. |
| [3] | 车闫瑾, 祁影霞, 潘帅, 王禹贺, 张华. 微通道脉管非线性交变振荡微观机理的分子动力学研究[J]. 计算物理, 2020, 37(5): 571-580. |
| [4] | 陈余, 邢永明. 静水压力对Al14Mn2P16磁光性质影响的密度泛函理论研究[J]. 计算物理, 2020, 37(2): 231-239. |
| [5] | 苏戈曼, 崔国民, 鲍中凯, 肖媛, 岑镇宇. 换热网络中温度交叉结构的分析与处理[J]. 计算物理, 2020, 37(1): 107-118. |
| [6] | 贺云龙, 李凌. 激光照射金颗粒在散射效应下的相变传热[J]. 计算物理, 2019, 36(2): 182-188. |
| [7] | 刘勇强, 査学军, 王清松, 杨振, 夏清豪, 吴斌. 局域热源对磁岛热输运的影响[J]. 计算物理, 2019, 36(2): 203-210. |
| [8] | 张克声, 张向群, 邵芳, 唐文勇. 多元可激发气体声弛豫频率的环境影响分析[J]. 计算物理, 2019, 36(1): 89-98. |
| [9] | 李细霞, 王丽, 戴海燕, 李长玉. 基于拓展分离变量法的非傅里叶传热研究[J]. 计算物理, 2018, 35(6): 685-692. |
| [10] | 祁鹏, 刘慧卿, 庞占喜, 刘化普, 陈宇. SAGD循环预热储层温度分析模型[J]. 计算物理, 2018, 35(1): 64-70. |
| [11] | 高英俊, 杨瑞琳, 黄礼琳, 刘瑶. 纳观尺度裂纹扩展微观机理的晶体相场法研究[J]. 计算物理, 2017, 34(4): 453-460. |
| [12] | 王然, 安连锁, 沈国清, 张世平. 基于正则化SVD算法的三维温度场声学重建[J]. 计算物理, 2015, 32(2): 195-201. |
| [13] | 李波, 甯波, 苏海洋, 刘虹, 位云生. 产水气井井筒温度压力计算方法[J]. 计算物理, 2014, 31(5): 573-580. |
| [14] | 高英俊, 罗志荣, 邓芊芊, 黄礼琳, 林葵. 韧性材料的微裂纹扩展与分叉的晶体相场模拟[J]. 计算物理, 2014, 31(4): 471-478. |
| [15] | 刘岩, 刘石, 雷兢, Schlaberg H I. 基于分子弛豫模型的混合气体多物理场二维重建算法[J]. 计算物理, 2014, 31(1): 67-74. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||
版权所有 © 《计算物理》编辑部
地址:北京市海淀区丰豪东路2号 邮编:100094 E-mail:jswl@iapcm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发
