基于格子玻尔兹曼方法的井筒热流固耦合数值模拟

doi:10.19596/j.cnki.1001-246x.8715

摘要/Abstract

摘要：

基于格子玻尔兹曼方法(LBM)建立一种求解井筒温度分布的模型。该模型可同时求解井筒内流体的温压耦合流动、流体流动中的强制热对流和井筒与地层的流固热交换三种效应的控制方程, 实现井筒内流体域流动场-流体域温度场-固体域温度场三场的耦合求解, 克服了传统模型井筒流速为定值的缺陷, 并且具有更广的适用范围。通过理论分析和对比分析, 验证模型的可靠性和精度。研究结果表明: 井筒内流体流速变化影响流体在井筒中的温度分布, 在产出条件下, 在同一深度处会造成流体中心温度高、流体边界处温度低的分布情况。流体沿井筒轴向的温度的下降趋势会经历缓-稳-缓三个阶段, 且此三个阶段受到流动雷诺数或者流体普朗特数的影响。

关键词: 井筒温度, 井筒压力, 格子玻尔兹曼, 普朗特数, 耦合计算

Abstract:

A model based on lattice Boltzmann method (LBM) is developed to solve the heat transfer problems in the wellbore, which can simultaneously solve the controlling equations of temperature-pressure coupled flow of fluid in the wellbore, forced thermal convection in fluid flow and fluid-solid heat exchange between the wellbore and the formation, so it can realize the coupling solution of fluid flow field, fluid temperature field and wellbore temperature field, and compared with the traditional model, it not only overcomes the defect that the velocity is constant in wellbore, but also has a wider scope of application and higher computational efficiency. The reliability and accuracy of the model have been verified by comparative analysis with previous studies. The results show that the change of fluid velocity in the wellbore affects the temperature distribution of the fluid in the wellbore. Under the production condition, the temperature distribution at the center of the fluid is high and the temperature at the boundary of the fluid is low at the same depth. The downward trend of fluid temperature along the shaft axis will go through three stages: slow, steady and slow, and these three stages are affected by flow Reynolds number or fluid Prandtl number.

Key words: wellbore temperature, wellbore pressure, lattice Boltzmann, Prandtl number, coupling simulation

中图分类号:

TE31

胡春余. 基于格子玻尔兹曼方法的井筒热流固耦合数值模拟[J]. 计算物理, 2024, 41(3): 316-324.

Chunyu HU. Lattice Boltzmann Model for Simulating Heat-fluid-solid Interaction in Wellbore[J]. Chinese Journal of Computational Physics, 2024, 41(3): 316-324.

图/表 12

图1 井筒结构示意图

Fig.1 Wellbore structure diagram

图2 含导热块的方腔自然对流示意图

Fig.2 Square medium containing discrete circular intrusions

表1 左壁面努森数对比

Table 1 Comparison of the Nusselt numbers on the left

λ_s/λ_f	本文	Ref.[25]	Ref.[26]	Ref.[22]
1	1.224	1.233	1.193	1.250
10	2.048	2.030	2.066	2.051
100	2.345	2.313	2.394	2.336

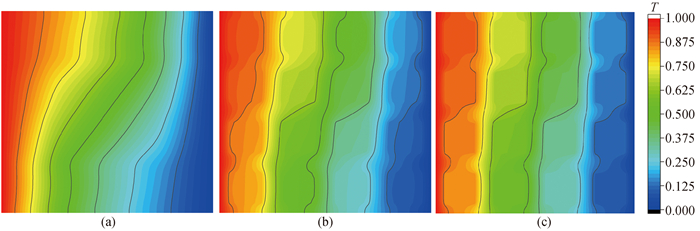
图3 含导热块方腔自然对流温度分布(a) λs/λf=1；(b) λs/λf=10；(c) λs/λf=100

Fig.3 Natural convection temperature distribution in square cavity with thermal conductive block at (a) λs/λf=1; (b) λs/λf=10; (c) λs/λf=100

表2 油田生产参数及准则数范围

Table 2 Typical range of oilfield production parameters and criterion number

油井深度/m	套管直径(外径)/mm	套管内径/mm	油管直径/mm	油管内径/mm	水泥环厚度/mm	Ra
1 000	177.8	159.4	73	62	32	10³~10⁹

油井日产液量	含水率/%	井底温度/℃	井口温度/℃	原油密度/(kg·m^-3)	原油运动黏度/ (m²·s^-1)	Re
1~100	0.1~99	40~60	20~30	800~1 000	50~10 × 10³	0.1~478

表3 准则数及模型参数

Table 3 Criterion number and model parameters

Pr	Ra	Re	下边界温度	上边界温度	径向网格数
1.0, 10, 100	10³, 10⁴, 10⁵	10, 100, 1 000	1.0	0.0	1 000

流体、环空导热系数	油管、套管导热系数	水泥环导热系数	地层导热系数	流体粘度	轴向网格数
1.0	319	4.42	15	0.01	1 000

图4 (a) 温度，(b) 密度和(c) 流速的分布云图

Fig.4 Distribution cloud map of (a) temperature; (b) density; (c) velocity

图5 井筒各部位中心点沿井筒轴向温度分布

Fig.5 Temperature distribution of the midpoint along the axial direction

图6 雷诺数对井筒径向温度分布的影响

Fig.6 Effect of Reynolds number on radial temperature distribution

图7 雷诺数对井筒轴向的流体温度分布的影响

Fig.7 Effect of Reynolds number on axial temperature distribution

图8 普朗特数对井筒径向温度分布的影响

Fig.8 Effect of Prandtl number on radial temperature distribution

图9 普朗特数对井筒轴向温度分布的影响

Fig.9 Effect of Prandtl number on axial temperature distribution

参考文献 26

1	RAMEY H J . Wellbore heat transmission[J]. Journal of Petroleum Technology, 1962, 14 (4): 427- 435. DOI
2	TANG Hewei , XU Boyue , HASAN A R , et al. Modeling wellbore heat exchangers: Fully numerical to fully analytical solutions[J]. Renewable Energy, 2019, 133, 1124- 1135. DOI
3	GUO Jianchun , LIU Zhuang , GOU Bo , et al. Study of wellbore heat transfer considering fluid rheological effects in deep well acidizing[J]. Journal of Petroleum Science and Engineering, 2020, 191, 107171. DOI
4	YANG Mou , LUO Dayu , CHEN Yuanhang , et al. Establishing a practical method to accurately determine and manage wellbore thermal behavior in high-temperature drilling[J]. Applied Energy, 2019, 238, 1471- 1483. DOI
5	ROOSTAIE M , LEONENKO Y . Analytical investigation of gas production from methane hydrates and the associated heat and mass transfer upon thermal stimulation employing a coaxial wellbore[J]. Energy Conversion and Management, 2020, 209, 112616. DOI
6	JAVADZADEGAN A , JOSHAGHANI M , MOSHFEGH A , et al. Accurate meso-scale simulation of mixed convective heat transfer in a porous media for a vented square with hot elliptic obstacle: An LBM approach[J]. Physica A: Statistical Mechanics and its Applications, 2020, 537, 122439. DOI
7	KRAVETS B , ROSEMANN T , REINECKE S R , et al. A new drag force and heat transfer correlation derived from direct numerical LBM-simulations of flown through particle packings[J]. Powder Technology, 2019, 345, 438- 456. DOI
8	ZHANG Ying , HUANG Yichen , XU Meng , et al. Flow and heat transfer simulation in a wall-driven porous cavity with internal heat source by multiple-relaxation time lattice Boltzmann method (MRT-LBM)[J]. Applied Thermal Engineering, 2020, 173, 115209. DOI
9	彭浩, 单鸣雷, 朱昌平, 等. LBM伪势MRT三维模型GPU并行计算的性能优化[J]. 计算物理, 2018, 35 (5): 554- 562.
10	孙金丛, 杜鹏, 李培生, 等. 基于LBM的部分热活跃边界下多孔腔体内自然对流换热[J]. 计算物理, 2017, 34 (5): 583- 592. DOI
11	董志强, 李维仲. 不同精度格式的格子Boltzmann热模型的传热分析[J]. 计算物理, 2009, 26 (1): 94- 100. DOI
12	喻西崇, 刘瑜, 宋永臣, 等. 基于LBM方法的天然气水合物沉积物中多相流动规律研究[J]. 中国石油大学学报(自然科学版), 2011, 35 (5): 99- 103. DOI
13	吴杰, 徐爽, 赵宁. 一种模拟大密度比多相流的混合算法[J]. 计算物理, 2013, 30 (1): 1- 10. DOI
14	SARITHA G , BANERJEE R . Development and application of a high density ratio pseudopotential based two-phase LBM solver to study cavitating bubble dynamics in pressure driven channel flow at low Reynolds number[J]. European Journal of Mechanics-B/Fluids, 2019, 75, 83- 96. DOI
15	SITOMPUL Y P , AOKI T . A filtered cumulant lattice Boltzmann method for violent two-phase flows[J]. Journal of Computational Physics, 2019, 390, 93- 120. DOI
16	WANG Kun , SUN W C . An updated Lagrangian LBM-DEM-FEM coupling model for dual-permeability fissured porous media with embedded discontinuities[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 344, 276- 305. DOI
17	WANG Yingda , CHUNG T , ARMSTRONG R T , et al. ML-LBM: Predicting and accelerating steady state flow simulation in porous media with convolutional neural networks[J]. Transport in Porous Media, 2021, 138 (1): 49- 75. DOI
18	SHAN Xiaowen . Simulation of Rayleigh-Bénard convection using a lattice Boltzmann method[J]. Physical Review E, 1997, 55 (3): 2780- 2788. DOI
19	郭照立, 郑楚光. 格子Boltzmann方法的原理及应用[M]. 北京: 科学出版社, 2009.
20	KARANI H , HUBER C . Lattice Boltzmann formulation for conjugate heat transfer in heterogeneous media[J]. Physical Review E, 2015, 91 (2): 023304. DOI
21	HU Yang , LI Decai , SHU Shi , et al. Full Eulerian lattice Boltzmann model for conjugate heat transfer[J]. Physical Review E, 2015, 92 (6): 063305. DOI
22	LU Jinhua , LEI Haiyan , DAI Chuanshan . A lattice Boltzmann algorithm for simulating conjugate heat transfer through virtual heat capacity correction[J]. International Journal of Thermal Sciences, 2017, 116, 22- 31. DOI
23	GUO Zhaoli , ZHENG Chuguang , SHI Baochang . Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method[J]. Chinese Physics, 2002, 11 (4): 366. DOI
24	何雅玲, 王勇, 李庆. 格子Boltzmann方法的理论及应用[M]. 北京: 科学出版社, 2009.
25	MERRIKH A A , LAGE J L . Natural convection in an enclosure with disconnected and conducting solid blocks[J]. International Journal of Heat and Mass Transfer, 2005, 48 (7): 1361- 1372. DOI
26	RAJI A , HASNAOUI M , NAÏMI M , et al. Effect of the subdivision of an obstacle on the natural convection heat transfer in a square cavity[J]. Computers & Fluids, 2012, 68, 1- 15.

[1]	王习文, 叶学民, 李丹, 李春曦. 大液滴撞击不同润湿性小球的三维格子Boltzmann方法模拟[J]. 计算物理, 2024, 41(2): 172-181.
[2]	张浏斌, 单彦广, 戎志成. 基于LBM的均匀电场池沸腾单气泡动力学模拟[J]. 计算物理, 2022, 39(5): 537-548.
[3]	郑江韬, 贾宁洪, 胡慧芳, 杨勇, 鞠杨, 王沫然. 分支通道内液-液自发渗吸规律研究[J]. 计算物理, 2021, 38(5): 543-554.
[4]	王子墨, 李凌. 超短激光打孔中快速相变的格子玻尔兹曼模拟[J]. 计算物理, 2020, 37(3): 299-306.
[5]	连小龙, 陈岳, 李培生, 张莹, 李伟, 刘强. 基于MRT-LB伪势模型的液滴撞击液膜数值研究[J]. 计算物理, 2020, 37(1): 79-87.
[6]	罗祝清, 娄钦, 徐洪涛, 杨茉. 热质双扩散与流固共轭传热及吸附的LBM模拟[J]. 计算物理, 2019, 36(1): 60-68.
[7]	周天, 李学敏, 刘峰. 二维平板间驻波声流的MRT-LBM数值研究[J]. 计算物理, 2018, 35(1): 39-46.
[8]	张东辉, 刘方贵, 张金存, 芮孝芳. 应用于非线性热传导方程的格子玻尔兹曼方法[J]. 计算物理, 2010, 27(5): 699-704.
[9]	陈瑜, 夏振华, 蔡庆东. 基于树网格的格子Boltzmann方法以及曲线边界的处理[J]. 计算物理, 2010, 27(1): 23-30.
[10]	聂小波. 激波的格子玻尔兹曼方法模拟[J]. 计算物理, 1998, 15(1): 1-5.
[11]	杭义洪, 陈贤林, 董振, 于志鲁, 范中波, 耿沪男. 石油射孔弹的数值模拟[J]. 计算物理, 1997, 14(S1): 404-406.