含裂缝线弹性问题的压缩预条件共轭梯度算法

doi:10.19596/j.cnki.1001-246x.8793

摘要/Abstract

摘要：

基于几何型扩展有限元离散, 研究含静态裂缝线弹性问题的高效压缩预条件算法。不仅构造适用于含裂缝线弹性问题的压缩子空间矩阵, 而且给出压缩点的选点原则。为进一步提高计算效率, 将该压缩技巧以乘性的方式与"裂尖型"区域分解预条件子相结合, 提出一类高效的自适应压缩预条件共轭梯度算法, 该算法能同时消去迭代求解中的高频误差和低频误差, 数值实验验证了算法的有效性。

关键词: 扩展有限元方法, 压缩技巧, 区域分解预条件子, 静态裂缝问题

Abstract:

This paper focuses on some efficient deflated preconditioners for static elastic crack problems modelled by the geometrical extended finite element method. We not only construct the deflation subspace matrix which is suitable for linear elastic crack problems, but also give the principle for selecting the deflated mesh nodes. To further accelerate the convergence, we combine the deflation technique with the "crack tip" domain decomposition preconditioners through multiplicative way, and propose efficient adapted deflated preconditioned conjugate gradient solvers which can eliminate the high-frequency and low-frequency errors simultaneously in the iterations. Numerical experiments demonstrate the effectiveness of our algorithm.

Key words: extended finite element method, deflation technique, domain decomposition preconditioners, static crack problems

中图分类号:

O357.41

刘杏康, 陈星玎, 余云龙. 含裂缝线弹性问题的压缩预条件共轭梯度算法[J]. 计算物理, 2024, 41(5): 619-629.

Xingkang LIU, Xingding CHEN, Yunlong YU. Deflated Preconditioned Conjugate Gradient Solvers for Linear Elastic Crack Problems[J]. Chinese Journal of Computational Physics, 2024, 41(5): 619-629.

图/表 13

图1 二维含裂缝线弹性体模型

Fig.1 A two-dimensional model of linear elastic body with a crack

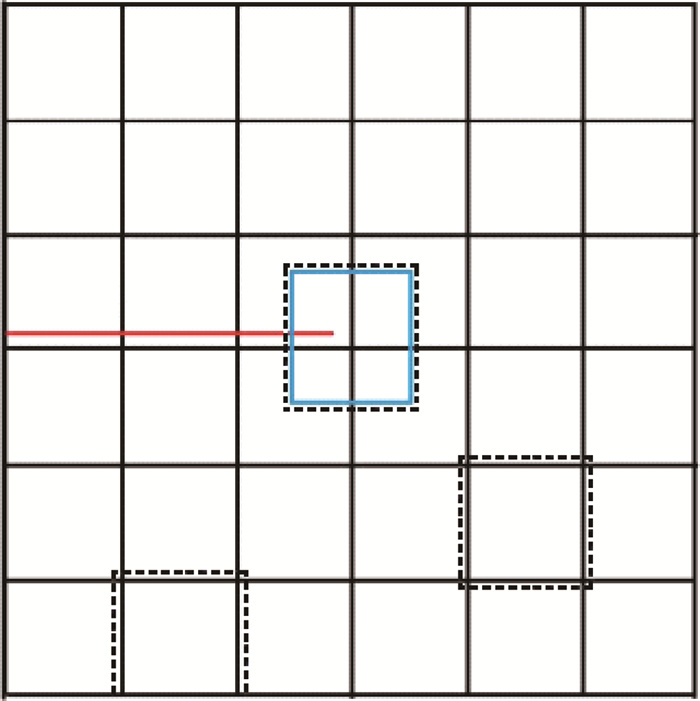
图2 “裂尖型”区域分解示意图(蓝色和黑色子区域分别代表裂尖子区域和常规子区域。)

Fig.2 Schematic of the "crack tip" domain decomposition (The blue subdomain denotes the "crack tip" subdomain, and the black subdomains denote "regular" subdomains.)

图3 单轴拉伸的边裂纹板模型

Fig.3 Model of uniaxial tensile single-edge crack plate

图4 几何型XFEM压缩子空间结点选取示意图(a) 网格剖分为39×39；(b) 只选择Heaviside增强结点；(c) 只选择裂尖增强结点；(d) 选择所有增强结点((b)~(d)为网格局部放大后的不同选点策略示意图。)

Fig.4 Schematic of deflation nodes selections in geometric XFEM (a) the mesh is dissected into 39×39; (b) only Heaviside enhancement nodes are selected; (c) only crack-tip enhancement nodes are selected; (d) all enhancement nodes are selected ((b)-(d) are the schematic representations of the different point selection strategies after local magnification.)

表1 选择不同压缩点的迭代次数

Table 1 The number of iterations for different selection of deflated nodes

网格剖分	CG_Jac	ADCG_H	ADCG_tip	ADCG_Htip
19×19	28	21	27	22
39×39	41	32	39	31
59×59	50	38	48	38
79×79	58	44	55	43
99×99	64	49	61	48
119×119	69	53	66	52
139×139	74	57	71	55

表2 不同选点策略所包含的结点个数

Table 2 The number of nodes included in different nodes selection strategies

网格剖分	ADCG_H	ADCG_tip	ADCG_Htip
19×19	16	12	28
39×39	32	52	84
59×59	48	112	160
79×79	64	192	256
99×99	80	308	388
119×119	96	448	544
139×139	112	608	720

图5 两子区域分解示意图

Fig.5 Decomposition schematic of two subdomains

表3 不同预条件子处理后M-1A的条件数(δ=2)

Table 3 The condition number of M-1A after different preconditioning (δ=2)

网格剖分	Cond_NPre	Cond_Jac	Cond_AS	Cond_RAS
19×19	2.25×10⁶	2.34×10⁵	8.24×10²	6.75×10²
39×39	1.62×10⁹	6.81×10⁷	1.04×10⁵	1.02×10⁵
59×59	3.05×10¹⁰	1.44×10⁹	1.23×10⁶	1.23×10⁶
79×79	1.86×10¹¹	1.08×10¹⁰	7.77×10⁶	7.76×10⁶
99×99	1.43×10¹²	1.35×10¹¹	5.08×10⁷	5.07×10⁷

表4 M-1取不同预条件子时，ADCG算法迭代步数(重叠度δ=2，E代表精确求解常规子区域。)

Table 4 The number of iterations of ADCG method using different preconditioners M-1 (Overlap δ=2 and E denotes exact solution in the regular domain.)

网格剖分	ADCG_Jac	ADCG_EAS	ADCG_ERAS	ADCG_AS	ADCG_RAS
19×19	21	3	3	3	3
39×39	32	5	5	5	5
59×59	38	7	7	9	10
79×79	44	9	10	11	12
99×99	49	13	13	16	18
119×119	53	13	16	20	22
139×139	57	15	17	23	25

表5 取不同重叠度δ时，ADCG算法迭代步数

Table 5 The number of iterations of ADCG method with different overlap δ

网格剖分	δ=1		δ=2		δ=3
网格剖分	ADCG_EAS	ADCG_ERAS	ADCG_EAS	ADCG_ERAS	ADCG_EAS	ADCG_ERAS
19×19	4	3	3	3	3	3
39×39	5	5	5	5	5	5
59×59	9	7	7	7	7	7
79×79	9	14	9	10	9	10
99×99	15	16	13	13	11	13
119×119	17	18	13	16	13	14
139×139	19	19	15	17	13	15

表6 多子区域划分下M RAS-1预条件CG算法的迭代步数

Table 6 The number of iterations for M RAS-1 preconditioned CG method with multi-subdomains

网格剖分	5×5		7×7		9×9
网格剖分	CG_ERAS	CG_RAS	CG_ERAS	CG_RAS	CG_ERAS	CG_RAS
39×39	21	23	28	29	27	31
59×59	25	27	30	32	35	42
79×79	29	37	33	48	39	60
99×99	32	42	37	56	43	86
119×119	36	43	39	57	48	93
139×139	38	60	43	68	48	101

表7 多子区域划分下采用不同预条件子的迭代步数

Table 7 The number of iterations for different preconditioners with multi-subdomains

网格剖分	ADCG_Jac	5×5		7×7		9×9
网格剖分	ADCG_Jac	ADCG_EAS	ADCG_ERAS	ADCG_EAS	ADCG_ERAS	ADCG_EAS	ADCG_ERAS
39×39	32	11	11	15	14	16	15
59×59	38	14	13	16	19	18	20
79×79	44	13	15	16	16	20	20
99×99	49	14	14	17	17	25	25
119×119	53	15	15	18	18	27	27
139×139	57	20	20	19	19	27	27

表8 多子区域划分下采用不同预条件子的迭代步数(常规子区域采用ILU非精确求解。)

Table 8 The number of iterations for different preconditioners with multi-subdomains (Inexact solutions using ILU are used in the regular domain.)

网格剖分	ADCG_Jac	5×5		7×7		9×9
网格剖分	ADCG_Jac	ADCG_AS	ADCG_RAS	ADCG_AS	ADCG_RAS	ADCG_AS	ADCG_RAS
39×39	32	11	11	14	14	16	16
59×59	38	12	14	17	17	18	21
79×79	44	14	13	16	16	20	20
99×99	49	16	14	17	17	25	25
119×119	53	21	15	21	21	29	26
139×139	57	22	20	22	22	28	27

参考文献 25

1	徐小文, 莫则尧, 胡少亮, 等. 特征修正并行预条件算法框架[J]. 计算物理, 2024, 41 (1): 64- 74.
2	杜旭林, 程林松, 牛烺昱, 等. 考虑水力压裂缝和天然裂缝动态闭合的三维离散缝网数值模拟[J]. 计算物理, 2022, 39 (4): 453- 464.
3	COLOMBO D , GIGLIO M . A methodology for automatic crack propagation modelling in planar and shell FE models[J]. Engineering Fracture Mechanics, 2006, 73 (4): 490- 504. DOI
4	余天堂. 扩展有限单元法——理论、应用及程序[M]. 北京: 科学出版社, 2014: 1- 12.
5	BELYTSCHKO T , BLACK T . Elastic crack growth in finite elements with minimal remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 45 (5): 601- 620. DOI
6	MOËS N , DOLBOW J , BELYTSCHKO T . A finite element method for crack growth without remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 46 (1): 131- 150. DOI
7	DAUX C , MOËS N , DOLBOW J , et al. Arbitrary branched and intersecting cracks with the extended finite element method[J]. International Journal for Numerical Methods in Engineering, 2000, 48 (12): 1741- 1760. DOI
8	MELENK J M , BABUŠKA I . The partition of unity finite element method: Basic theory and applications[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139 (1/4): 289- 314.
9	BABUŠKA I , BANERJEE U . Stable generalized finite element method (SGFEM)[J]. Computer Methods in Applied Mechanics and Engineering, 2012, 201/204, 91- 111. DOI
10	GUPTA V , DUARTE C A , BABUŠKA I , et al. A stable and optimally convergent generalized FEM (SGFEM) for linear elastic fracture mechanics[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 266, 23- 39. DOI
11	ZHANG Qinghui , BABUŠKA I , BANERJEE U . Robustness in stable generalized finite element methods (SGFEM) applied to Poisson problems with crack singularities[J]. Computer Methods in Applied Mechanics and Engineering, 2016, 311, 476- 502. DOI
12	TIAN Rong , WEN Longfei , WANG Lixiang . Three-dimensional improved XFEM (IXFEM) for static crack problems[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 343, 339- 367. DOI
13	MENK A , BORDAS S P A . A robust preconditioning technique for the extended finite element method[J]. International Journal for Numerical Methods in Engineering, 2011, 85 (13): 1609- 1632. DOI
14	BERGER-VERGIAT L , WAISMAN H , HIRIYUR B , et al. Inexact Schwarz-algebraic multigrid preconditioners for crack problems modeled by extended finite element methods[J]. International Journal for Numerical Methods in Engineering, 2012, 90 (3): 311- 328. DOI
15	CHEN Xingding , CAI Xiaochuan . Effective two-level domain decomposition preconditioners for elastic crack problems modeled by extended finite element method[J]. Communications in Computational Physics, 2020, 28 (4): 1561- 1584. DOI
16	AGATHOS K , DODWELL T , CHATZI E , et al. An adapted deflated conjugate gradient solver for robust extended/generalised finite element solutions of large scale, 3D crack propagation problems[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 395, 114937. DOI
17	SAAD Y , YEUNG M , ERHEL J , et al. A deflated version of the conjugate gradient algorithm[J]. SIAM Journal on Scientific Computing, 2000, 21 (5): 1909- 1926. DOI
18	NICOLAIDES R A . Deflation of conjugate gradients with applications to boundary value problems[J]. SIAM Journal on Numerical Analysis, 1987, 24 (2): 355- 365. DOI
19	TANG J M, NABBEN R, VUIK C, et al. Theoretical and numerical comparison of various projection methods derived from deflation, domain decomposition and multigrid methods: REPORT 07-04[R]. Delft: Delft University of Technology, 2007.
20	PARKS M L , DE STURLER E , MACKEY G , et al. Recycling Krylov subspaces for sequences of linear systems[J]. SIAM Journal on Scientific Computing, 2006, 28 (5): 1651- 1674. DOI
21	DIAZ CORTES G B , VUIK C , JANSEN J D . On POD-based deflation vectors for DPCG applied to porous media problems[J]. Journal of Computational and Applied Mathematics, 2018, 330, 193- 213. DOI
22	李开泰, 黄艾香, 黄庆怀. 有限元方法及其应用[M]. 北京: 科学出版社, 2006: 54- 64.
23	AUBRY R , MUT F , DEY S , et al. Deflated preconditioned conjugate gradient solvers for linear elasticity[J]. International Journal for Numerical Methods in Engineering, 2011, 88 (11): 1112- 1127. DOI
24	CAI Xiaochuan , SARKIS M . A restricted additive schwarz preconditioner for general sparse linear systems[J]. SIAM Journal on Scientific Computing, 1999, 21 (2): 792- 797. DOI
25	范鹤潇, 陈星玎. 一类求解含静态裂缝线弹性问题的预条件扩展有限元方法[J]. 计算物理, 2024, 41 (2): 151- 160.