计算物理 ›› 2024, Vol. 41 ›› Issue (2): 151-160.DOI: 10.19596/j.cnki.1001-246x.8683
收稿日期:2022-12-15
出版日期:2024-03-25
发布日期:2024-04-03
通讯作者:
陈星玎
作者简介:范鹤潇, 男, 硕士研究生, 研究方向为偏微分方程数值解, E-mail: 2030101007@st.btbu.edu.cn
基金资助:
Hexiao FAN( ), Xingding CHEN(
), Xingding CHEN( )
)
Received:2022-12-15
Online:2024-03-25
Published:2024-04-03
Contact:
Xingding CHEN
摘要:
基于几何型扩展有限元离散方法, 研究含静态裂缝线弹性问题的高效区域分解预条件算法。为了构造Schwarz型预条件算法, 采用一种特殊的裂尖型区域分解策略, 将计算区域分解为包含所有分支增强自由度的裂尖子区域和仅包含标准有限元自由度与Heaviside增强自由度的常规子区域。基于该区域分解策略, 推导一类高效的乘性和限制型乘性Schwarz区域分解预条件子, 对裂尖子问题进行精确求解, 而对常规子问题则非精确求解。数值实验验证了算法的有效性。
中图分类号:
范鹤潇, 陈星玎. 一类求解含静态裂缝线弹性问题的预条件扩展有限元方法[J]. 计算物理, 2024, 41(2): 151-160.
Hexiao FAN, Xingding CHEN. A Class of Preconditioners for Static Elastic Crack Problems Modeled by Extended Finite Element Method[J]. Chinese Journal of Computational Physics, 2024, 41(2): 151-160.
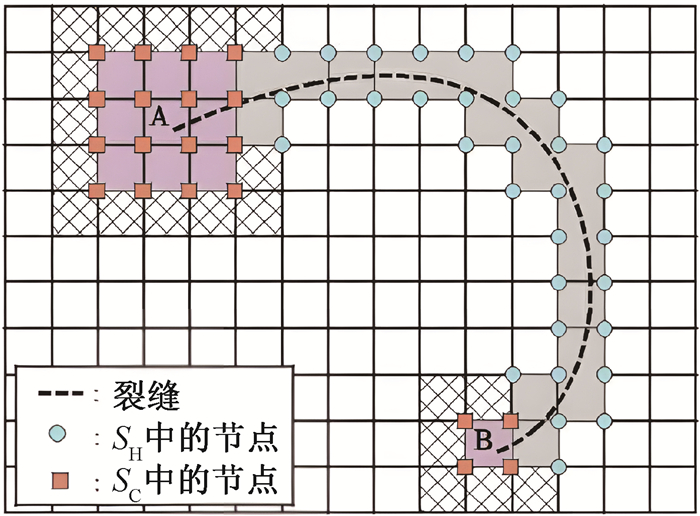
图2 结构化网格中的裂缝(圆点和方点分属裂缝增强节点集合SH和裂尖增强节点集合SC。)
Fig.2 Crack located on a structured mesh (Nodes in sets SH and SC are denoted by circles and squares, respectively.)
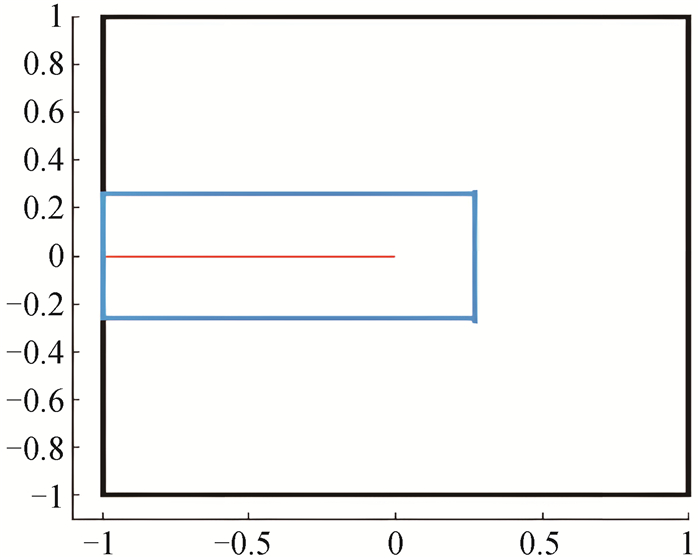
图3 裂缝型区域分解(红线代表裂缝,蓝色子区域代表裂缝子区域,其余部分为好子区域。)
Fig.3 Schematic representation of two subdomains in the "crack line" domain decomposition (The red line denotes cracks, the blue subdomain denotes the "cracked" domain, the other is the "healthy" domain.)
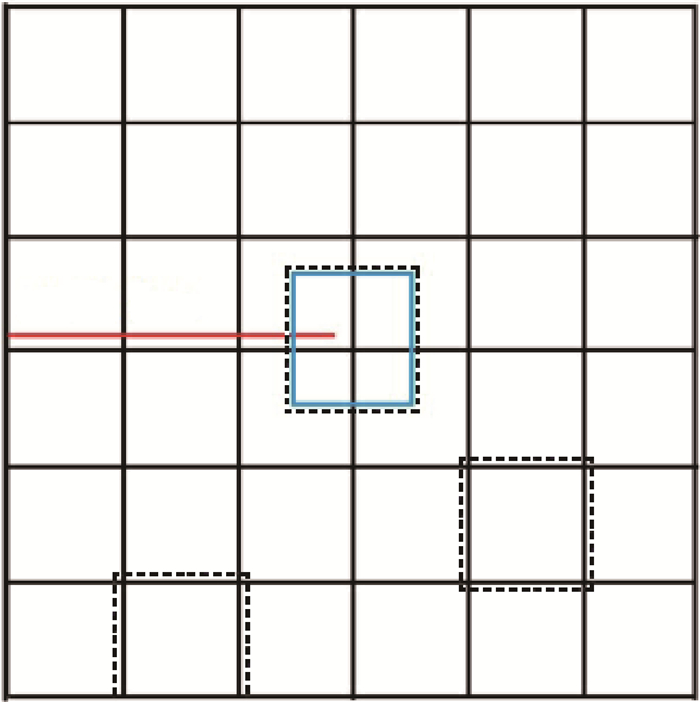
图4 裂尖型区域分解(蓝色和黑色子区域分别代表裂尖子区域和常规子区域。)
Fig.4 Schematic representation of subdomains in the "crack tip" domain decomposition(The blue subdomain denotes the "crack tip" domain, the black subdomains denote "regular" domains.)
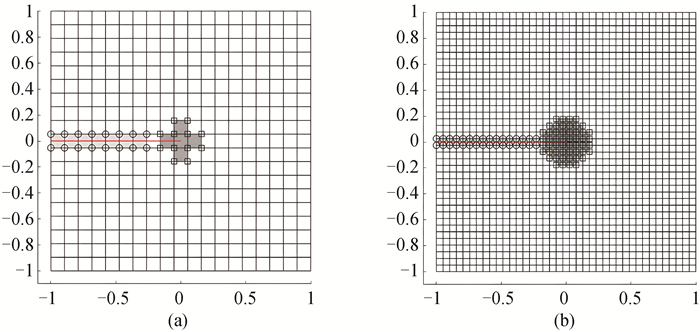
图6 几何型XFEM示意图(圆点和方点分属裂缝增强节点集合SH和裂尖增强节点集合SG,红线代表裂缝线。) (a) 网格剖分为19×19;(b) 网格剖分为39×39
Fig.6 The geometric XFEM (The red line denotes the crack, nodes in sets SH and SG are denoted by circles and squares, respectively.) (a) the mesh scale is 19×19; (b) the mesh scale is 39×39
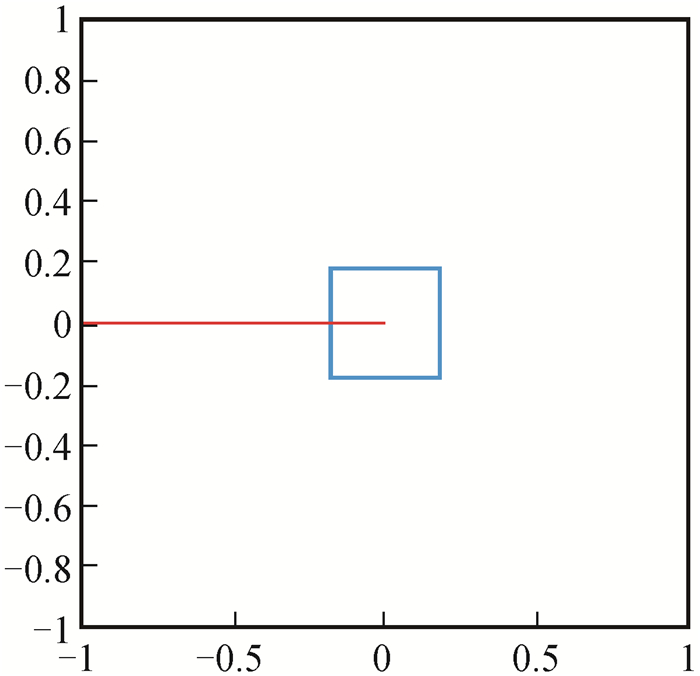
图7 两子区域问题示意图(红线代表裂缝线,蓝色区域为裂尖子区域。)
Fig.7 Schematic representation of two subdomains in the domain decomposition (The red line denotes cracks, the blue subdomain denotes the "crack tip" domain.)
| 网格剖分 | CondNPre | CondRAS | CondRMS |
| 19×19 | 3.08×106 | 7.40×103 | 8.92×103 |
| 39×39 | 1.62×109 | 3.10×106 | 3.76×106 |
| 59×59 | 3.05×1010 | 4.22×107 | 5.05×107 |
| 79×79 | 2.13×1011 | 2.19×108 | 2.66×108 |
| 99×99 | 1.43×1012 | 6.46×108 | 1.20×109 |
| 119×119 | 4.83×1012 | 3.10×109 | 3.74×109 |
表1 两子区域问题的总刚度矩阵条件数(δ=2,CondNPre、CondRAS、CondRMS分别代表无预条件子,采用RAS预条件和采用RMS预条件后总刚度矩阵的条件数。)
Table 1 The condition number of the stiffness matrix for the two subdomains preconditioner (δ=2, CondNPre, CondRAS, CondRMS denotes condition number of the stiffness matrix with no preconditioner, with RAS preconditioner and with RMS preconditioner respectively.)
| 网格剖分 | CondNPre | CondRAS | CondRMS |
| 19×19 | 3.08×106 | 7.40×103 | 8.92×103 |
| 39×39 | 1.62×109 | 3.10×106 | 3.76×106 |
| 59×59 | 3.05×1010 | 4.22×107 | 5.05×107 |
| 79×79 | 2.13×1011 | 2.19×108 | 2.66×108 |
| 99×99 | 1.43×1012 | 6.46×108 | 1.20×109 |
| 119×119 | 4.83×1012 | 3.10×109 | 3.74×109 |
| 网格剖分 | NonPre | EAS | ERAS | EMS | ERMS |
| 19×19 | 594 | 8 | 8 | 4 | 4 |
| 39×39 | 2 437 | 10 | 11 | 5 | 6 |
| 59×59 | 2 657 | 13 | 14 | 7 | 7 |
| 79×79 | 3 106 | 15 | 15 | 8 | 8 |
| 99×99 | 3 651 | 16 | 17 | 8 | 9 |
| 119×119 | 3 659 | 18 | 18 | 9 | 10 |
表2 两子区域问题迭代步数(NonPre代表无预条件子,E代表在常规子区域精确求解。)
Table 2 Number of iterations for two subdomains preconditioner (NonPre denotes no preconditioner, E denotes exact solution in the "regular" domain.)
| 网格剖分 | NonPre | EAS | ERAS | EMS | ERMS |
| 19×19 | 594 | 8 | 8 | 4 | 4 |
| 39×39 | 2 437 | 10 | 11 | 5 | 6 |
| 59×59 | 2 657 | 13 | 14 | 7 | 7 |
| 79×79 | 3 106 | 15 | 15 | 8 | 8 |
| 99×99 | 3 651 | 16 | 17 | 8 | 9 |
| 119×119 | 3 659 | 18 | 18 | 9 | 10 |
| 网格剖分 | AS | RAS | MS | RMS |
| 19×19 | 13 | 11 | 7 | 8 |
| 39×39 | 19 | 19 | 13 | 14 |
| 59×59 | 25 | 25 | 19 | 20 |
| 79×79 | 37 | 38 | 26 | 26 |
| 99×99 | 55 | 56 | 45 | 47 |
| 119×119 | 84 | 86 | 57 | 60 |
表3 两子区域问题迭代步数(在常规子区域采用ILU非精确求解,调降容差是10-3。)
Table 3 Number of iterations for two subdomains preconditioner (Inexact solution by using ILU decomposition with a 10-3 drop tolerance in the "regular" domain.)
| 网格剖分 | AS | RAS | MS | RMS |
| 19×19 | 13 | 11 | 7 | 8 |
| 39×39 | 19 | 19 | 13 | 14 |
| 59×59 | 25 | 25 | 19 | 20 |
| 79×79 | 37 | 38 | 26 | 26 |
| 99×99 | 55 | 56 | 45 | 47 |
| 119×119 | 84 | 86 | 57 | 60 |
| 网格剖分 | NonPre | EAS | ERAS | EMS | ERMS |
| 39×39 | 2 437 | 31 | 26 | 27 | 24 |
| 59×59 | 2 657 | 38 | 33 | 34 | 29 |
| 79×79 | 3 106 | 43 | 37 | 38 | 35 |
| 99×99 | 3 651 | 51 | 41 | 42 | 38 |
| 119×119 | 3 659 | 56 | 46 | 48 | 42 |
| 139×139 | 3 599 | 63 | 50 | 53 | 46 |
| 159×159 | 3 622 | 69 | 54 | 58 | 49 |
表4 采用不同预条件子的迭代步数(常规子区域为4×4个,精确求解,δ=1。)
Table 4 Number of iterations for different preconditioners with a 4×4 patition, δ=1
| 网格剖分 | NonPre | EAS | ERAS | EMS | ERMS |
| 39×39 | 2 437 | 31 | 26 | 27 | 24 |
| 59×59 | 2 657 | 38 | 33 | 34 | 29 |
| 79×79 | 3 106 | 43 | 37 | 38 | 35 |
| 99×99 | 3 651 | 51 | 41 | 42 | 38 |
| 119×119 | 3 659 | 56 | 46 | 48 | 42 |
| 139×139 | 3 599 | 63 | 50 | 53 | 46 |
| 159×159 | 3 622 | 69 | 54 | 58 | 49 |
| 网格剖分 | EAS | ERAS | EMS | ERMS |
| 39×39 | 28 | 22 | 24 | 20 |
| 59×59 | 30 | 26 | 26 | 24 |
| 79×79 | 35 | 29 | 30 | 27 |
| 99×99 | 39 | 33 | 34 | 30 |
| 119×119 | 42 | 36 | 37 | 34 |
| 139×139 | 47 | 39 | 39 | 35 |
| 159×159 | 52 | 41 | 43 | 38 |
表5 采用不同预条件子的迭代步数(常规子区域为4×4个,精确求解,δ=2。)
Table 5 Number of iterations for different preconditioners with a 4×4 patition, δ=2
| 网格剖分 | EAS | ERAS | EMS | ERMS |
| 39×39 | 28 | 22 | 24 | 20 |
| 59×59 | 30 | 26 | 26 | 24 |
| 79×79 | 35 | 29 | 30 | 27 |
| 99×99 | 39 | 33 | 34 | 30 |
| 119×119 | 42 | 36 | 37 | 34 |
| 139×139 | 47 | 39 | 39 | 35 |
| 159×159 | 52 | 41 | 43 | 38 |
| 网格剖分 | 4×4 | 6×6 | 8×8 | ||||||||
| ERAS | EMS | ERMS | ERAS | EMS | ERMS | ERAS | EMS | ERMS | |||
| 39×39 | 22 | 24 | 20 | 26 | 29 | 23 | 30 | 29 | 29 | ||
| 59×59 | 26 | 26 | 24 | 32 | 35 | 28 | 37 | 41 | 34 | ||
| 79×79 | 29 | 30 | 27 | 36 | 41 | 35 | 41 | 47 | 37 | ||
| 99×99 | 33 | 34 | 30 | 41 | 50 | 38 | 47 | 57 | 42 | ||
| 119×119 | 36 | 37 | 34 | 44 | 48 | 41 | 53 | 63 | 48 | ||
| 139×139 | 39 | 39 | 35 | 48 | 55 | 45 | 58 | 71 | 54 | ||
| 159×159 | 41 | 43 | 38 | 55 | 59 | 51 | 63 | 72 | 58 | ||
表6 不同区域分解下不同预条件的迭代步数(δ=2,常规子区域精确求解。)
Table 6 Number of iterations for different preconditioners with different patitions (δ=2, exact solutions in "regular" domains.)
| 网格剖分 | 4×4 | 6×6 | 8×8 | ||||||||
| ERAS | EMS | ERMS | ERAS | EMS | ERMS | ERAS | EMS | ERMS | |||
| 39×39 | 22 | 24 | 20 | 26 | 29 | 23 | 30 | 29 | 29 | ||
| 59×59 | 26 | 26 | 24 | 32 | 35 | 28 | 37 | 41 | 34 | ||
| 79×79 | 29 | 30 | 27 | 36 | 41 | 35 | 41 | 47 | 37 | ||
| 99×99 | 33 | 34 | 30 | 41 | 50 | 38 | 47 | 57 | 42 | ||
| 119×119 | 36 | 37 | 34 | 44 | 48 | 41 | 53 | 63 | 48 | ||
| 139×139 | 39 | 39 | 35 | 48 | 55 | 45 | 58 | 71 | 54 | ||
| 159×159 | 41 | 43 | 38 | 55 | 59 | 51 | 63 | 72 | 58 | ||
| 网格剖分 | 4×4 | 6×6 | 8×8 | ||||||||
| RAS | MS | RMS | RAS | MS | RMS | RAS | MS | RMS | |||
| 39×39 | 24 | 26 | 22 | 27 | 29 | 24 | 32 | 29 | 26 | ||
| 59×59 | 34 | 36 | 30 | 40 | 39 | 34 | 41 | 42 | 38 | ||
| 79×79 | 47 | 47 | 43 | 49 | 48 | 45 | 50 | 52 | 46 | ||
| 99×99 | 57 | 59 | 54 | 56 | 62 | 54 | 58 | 64 | 55 | ||
| 119×119 | 77 | 75 | 72 | 74 | 73 | 69 | 75 | 75 | 70 | ||
| 139×139 | 85 | 84 | 82 | 86 | 83 | 81 | 86 | 87 | 82 | ||
| 159×159 | 109 | 109 | 106 | 115 | 117 | 110 | 104 | 107 | 101 | ||
表7 不同区域分解下预条件GMRES迭代步数(δ=2,常规子区域采用ILU非精确求解。)
Table 7 Number of iterations for different preconditioners with different patitions (δ=2, inexact solutions using ILU decomposition with a 10-3 drop tolerance in the "regular" domain.)
| 网格剖分 | 4×4 | 6×6 | 8×8 | ||||||||
| RAS | MS | RMS | RAS | MS | RMS | RAS | MS | RMS | |||
| 39×39 | 24 | 26 | 22 | 27 | 29 | 24 | 32 | 29 | 26 | ||
| 59×59 | 34 | 36 | 30 | 40 | 39 | 34 | 41 | 42 | 38 | ||
| 79×79 | 47 | 47 | 43 | 49 | 48 | 45 | 50 | 52 | 46 | ||
| 99×99 | 57 | 59 | 54 | 56 | 62 | 54 | 58 | 64 | 55 | ||
| 119×119 | 77 | 75 | 72 | 74 | 73 | 69 | 75 | 75 | 70 | ||
| 139×139 | 85 | 84 | 82 | 86 | 83 | 81 | 86 | 87 | 82 | ||
| 159×159 | 109 | 109 | 106 | 115 | 117 | 110 | 104 | 107 | 101 | ||
| 1 | 高英俊, 罗志荣, 邓芊芊, 等. 韧性材料的微裂纹扩展与分叉的晶体相场模拟[J]. 计算物理, 2014, 31 (4): 471- 478. |
| 2 | 黄朝琴, 姚军, 王月英, 等. 基于离散裂缝模型的裂缝性油藏注水开发数值模拟[J]. 计算物理, 2011, 28 (1): 41- 49. |
| 3 | 李开泰, 黄艾香, 黄庆怀. 有限元方法及其应用[M]. 北京: 科学出版社, 2005: 1- 160. |
| 4 |
BELYTSCHKO T , BLACK T . Elastic crack growth in finite elements with minimal remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 45 (5): 601- 620.
DOI |
| 5 | 庄茁, 柳占立, 成斌斌, 等. 扩展有限单元法[M]. 北京: 清华大学出版社, 2012: 35- 47. |
| 6 | 杨璞, 牛红攀, 肖世富. 平面应变问题广义有限元法[J]. 计算物理, 2016, 33 (3): 358- 366. |
| 7 | BABUŠKA I , BANERJEE U . Stable generalized finite element method (SGFEM)[J]. Computer Methods in Applied Mechanics & Engineering, 2011, 201 (1): 91- 111. |
| 8 | GUPTA V , DUARTE C A , BABUŠKA I , et al. A stable and optimally convergent generalized FEM (SGFEM) for linear elastic fracture mechanics[J]. Computer Methods in Applied Mechanics & Engineering, 2013, 266 (1): 23- 39. |
| 9 | ZHANG Q H , BABUŠKA I , BANERJEE U . Robustness in stable generalized finite element methods (SGFEM) applied to Poisson problems with crack singularities[J]. Computer Methods in Applied Mechanics & Engineering, 2016, 311 (1): 476- 502. |
| 10 | 田荣, 文龙飞. 改进型XFEM进展[J]. 计算力学学报, 2016, 33 (4): 469- 477. |
| 11 |
ZHANG Q H . DOF-gathering stable generalized finite element methods for crack problems[J]. Numerical Methods for Partial Differential Equations, 2020, 36 (6): 1209- 1233.
DOI |
| 12 |
MENK A , BORDAS S P A . A robust preconditioning technique for the extended finite element method[J]. International Journal for Numerical Methods in Engineering, 2011, 85 (13): 1609- 1632.
DOI |
| 13 | LANG C , MAKHIJA D , DOOSTAN A , et al. A simple and efficient preconditioning scheme for heaviside enriched XFEM[J]. Computational Mechanics: Solids, Fluids, Fracture Transport Phenomena and Variational Methods, 2014, 54 (5): 1357- 1374. |
| 14 | GILBERT S . Computational science and engineering[M]. Wellesley, MA: Wellesley-Cambridge Press, 2007: 551- 597. |
| 15 |
WAISMAN H , BERGER-VERGIAT L . An adaptive domain decomposition preconditioner for crack propagation problems modeled by XFEM[J]. International Journal for Multiscale Computational Engineering, 2013, 11 (6): 633- 654.
DOI |
| 16 |
BERGER-VERGIAT L , WAISMAN H , HIRIYUR B , et al. Inexact Schwarz-algebraic multigrid preconditioners for crack problems modeled by extended finite element methods[J]. International Journal for Numerical Methods in Engineering, 2012, 90 (3): 311- 328.
DOI |
| 17 | TIAN R, WEN L F. An extra dof-free and well-conditioned XFEM[C]//Proceedings of the 5th International Conference on Computational Methods, 2014: 784-793. |
| 18 |
TIAN W , HUANG J J , JIANG Y , et al. A parallel scalable domain decomposition preconditioner for elastic crack simulation using XFEM[J]. International Journal for Numerical Methods in Engineering, 2022, 123 (15): 3393- 3417.
DOI |
| 19 |
GUPTA V , DUARTE C A , BABUŠKA I , et al. Stable GFEM (SGFEM): Improved conditioning and accuracy of GFEM/XFEM for three-dimensional fracture mechanics[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 289, 355- 386.
DOI |
| 20 |
GUPTA V , DUARTE C A , BABUŠKA I , et al. A stable and optimally convergent generalized FEM (SGFEM) for linear elastic fracture mechanics[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 266, 23- 39.
DOI |
| 21 | SAAD Y . Iterative methods for sparse linear systems[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2000: 157- 218. |
| 22 |
CAI X C , CHEN X D . Effective two-level domain decomposition preconditioners for elastic crack problems modeled by extended finite element method[J]. Communications in Computational Physics, 2020, 28 (4): 1561- 1584.
DOI |
| [1] | 舒适, 岳孝强, 何剑萌, 徐小文, 莫则尧. 多群辐射扩散问题特征驱动的并行AMG法[J]. 计算物理, 2024, 41(1): 87-97. |
| [2] | 尹亮, 杨超, 马石庄. 地球外核热对流运动的区域分解多重网格并行数值模拟[J]. 计算物理, 2019, 36(1): 1-14. |
| [3] | 田炜, 任新成. 雪层覆盖地面电磁散射的矩量法[J]. 计算物理, 2018, 35(2): 205-211. |
| [4] | 李刚, 张宝印, 邓力, 上官丹骅, 李瑞, 马彦, 付元光, 胡小利. 蒙特卡罗区域分解并行计算中确保串并行结果一致的伪随机数应用[J]. 计算物理, 2017, 34(1): 67-72. |
| [5] | 叶珍宝, 周海京. 高阶间断伽辽金时域有限元方法分析三维谐振腔[J]. 计算物理, 2015, 32(4): 449-454. |
| [6] | 陈学, 孙创, 夏新林. 基于区域分解和逐级光线分裂的杂散光分析[J]. 计算物理, 2012, 29(6): 876-880. |
| [7] | 周志阳, 徐小文, 舒适, 冯春生, 莫则尧. 二维三温辐射扩散方程组两层预条件子的自适应求解[J]. 计算物理, 2012, 29(4): 475-483. |
| [8] | 魏军侠, 袁光伟, 阳述林, 申卫东. 二维柱几何非定常中子输运方程基于格式的界面预估校正并行算法[J]. 计算物理, 2012, 29(2): 198-204. |
| [9] | 盛志明, 崔霞, 刘兴平. 扩散方程区域分解的多步算法[J]. 计算物理, 2011, 28(6): 825-830. |
| [10] | 周志阳, 聂存云, 舒适. 一种二阶混合有限体元格式的GAMG预条件子[J]. 计算物理, 2011, 28(4): 493-500. |
| [11] | 尚月强, 何银年. 非定常Navier-Stokes方程基于完全重叠型区域分解的有限元并行算法[J]. 计算物理, 2011, 28(2): 181-187. |
| [12] | 魏军侠, 阳述林, 傅连祥. 二维柱几何中子输运方程的并行区域分解方法[J]. 计算物理, 2010, 27(1): 1-7. |
| [13] | 刘鹏. 三维粗糙面电磁双站散射的直接型区域分解计算[J]. 计算物理, 2010, 27(1): 73-81. |
| [14] | 范宣华, 吴瑞安, 郝志明, 何颖波. 基于Tahoe框架的某夹具并行计算[J]. 计算物理, 2009, 26(5): 699-702. |
| [15] | 徐小文, 莫则尧, 安恒斌. 求解二维三温辐射扩散方程组的一种代数两层迭代方法[J]. 计算物理, 2009, 26(1): 1-8. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||
版权所有 © 《计算物理》编辑部
地址:北京市海淀区丰豪东路2号 邮编:100094 E-mail:jswl@iapcm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发
