考虑级联失效与恢复接续性的复杂网络恢复动力学

doi:10.19596/j.cnki.1001-246x.8677

摘要/Abstract

摘要：

为帮助网络系统在级联失效后尽快以合理投入实现恢复, 采用耦合映象格子作为恢复动力学模型基础, 将级联失效作用下的失效状态、耦合系数等作为恢复动力学输入, 建模过程中添加外部恢复力及内部耦合作用形成恢复动力学方法, 与未考虑接续性的3组网络恢复方法相比, 恢复效果分别提升了46.7%、47.9%和66.7%。在6组不同网络上的仿真实验结果表明: 本方法能拟合现实恢复场景, 并能克服网络在层级、规模、建网方法等方面的差异; 在三层交通网络中, 初始恢复比例对恢复程度的边际贡献率可达26.8%, 恢复耦合系数为0.5且首次恢复10%的节点时, 网络恢复程度最高达到86.4%;该恢复动力学方法可有效刻画多种网络的恢复行为。

关键词: 复杂网络, 级联动力学, 耦合映象格子, Henon映射

Abstract:

To help the network system restore with reasonable investment as soon as possible after cascading failure, using coupling map lattice as the basis of the restoration dynamics model, and the failure state and coupling coefficient under the cascade failure are taken as the input of the restoration dynamics. By further adding the external restoring force and the internal coupling to form the restoration dynamics method. The restoration effect is improved by 46.7%, 47.9% and 66.7% respectively compared with three groups of network restoration methods without considering continuity. In addition, the simulation results on six different networks show that this method can fit the real restoration scene, overcome the differences in network level, scale, network construction methods and so on. Specifically, in the three-layer transportation network, the marginal contribution rate of the initial restoration ratio to the restoration degree is 26.8%, and when the coupling coefficient of restoration is 0.5 and 10% of the nodes are restored for the first time, the restoration degree of the network is as high as 86.4%. The proposed restoration dynamics method can effectively describe the restoration process of various networks.

Key words: complex network, cascade dynamics, coupled map lattice, Henon mapping

中图分类号:

O414.2
U113

朱璋元, 王秋玲. 考虑级联失效与恢复接续性的复杂网络恢复动力学[J]. 计算物理, 2024, 41(2): 258-267.

Zhangyuan ZHU, Qiuling WANG. Complex Network Restoration Dynamics Method Considering Continuity between Cascading Failure and Restoration[J]. Chinese Journal of Computational Physics, 2024, 41(2): 258-267.

图/表 14

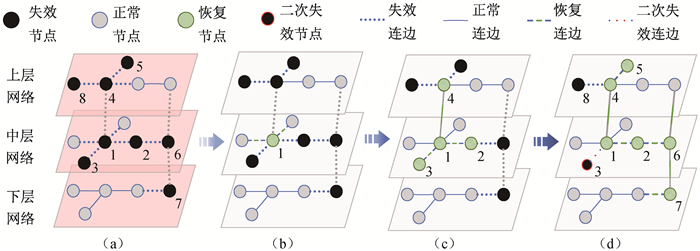
图1 失效网络的恢复动力学过程(a)失效稳定；(b)恢复开始；(c)恢复进行；(d)恢复结束

Fig.1 Dynamic process of network restoration from failure (a) stable failure state; (b) start of restoration; (c) process of restoration; (d) end of restoration

图2 级联失效与恢复过程的接续关系曲线

Fig.2 Continuation curve of cascading failure and restoration process

表1 对照实验结果

Table 1 Comparative experimental results

网络属性	方法	RL值
节点数=500 平均度=4	本文	2.43
节点数=500 平均度=4	Ref.[14]	4.56

节点数=1 000 平均度=6	本文	2.49
	Ref.[12]	4.78
	Ref.[20]	7.48

图3 三层交通复杂网络

Fig.3 Three-layer traffic complex network

表2 初始参数设置

Table 2 Initial parameter setting

参数	符号	取值
节点初始状态	x_i(t₀)	0.7
结构耦合系数	ε₁	0.3
失效仿真步长	c₁	100
指标比例系数	ω₁	0.5
恢复节点比例	o	10%
恢复耦合系数	ε_r	0.3
时间容忍度	T₁	3
恢复仿真步长	c₂	100

图4 失效节点状态分布

Fig.4 State distribution of failure nodes

图5 网络恢复仿真效果与实际结果

Fig.5 Network simulation restoration results

图6 恢复节点比例对恢复程度的影响

Fig.6 Effect of restoration node ratio on restoration degree

图7 耦合系数对恢复效果的影响

Fig.7 Influence of coupling coefficient on restoration effect

表3 网络拓扑参数

Table 3 Network topology parameters

网络编号	节点数	连边数	平均度	平均聚类系数
①	356	10 657	29.935	0.56
②	90	488	5.422	0.25
③	92	1 554	16.891	0.54

图8 实验2交通网络可视化 (a) 网络①；(b) 网络②；(c) 网络③

Fig.8 Visualization of traffic network (a) Network ①; (b) Network ②; (c) Network ③

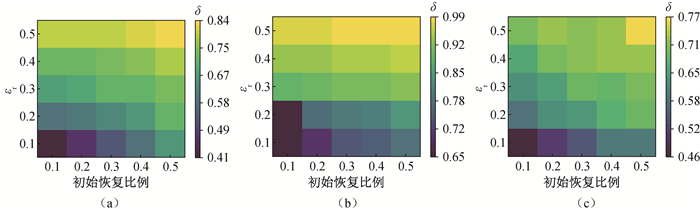
图9 初始恢复比例与恢复耦合系数变化关系 (a)网络①；(b)网络②；(c)网络③

Fig.9 Relationship between initial restoration ratio and restoration coupling coefficient (a) Network ①; (b) Network ②; (c) Network ③

图10 电力网络恢复过程

Fig.10 Power network restoration process

图11 生物网络恢复过程

Fig.11 Biological network restoration process

参考文献 27

1	LI H Q , ZOU Y L , ZHANG S Z , et al. Robustness of power grids structure and braess paradox phenomenon: A complex network theory study[J]. Chinese Journal of Computational Physics, 2021, 38 (4): 470- 478.
2	GAO C , FAN Y , JIANG S , et al. Dynamic robustness analysis of a two-layer rail transit network model[J]. IEEE Transactions on Intelligent Transportation Systems, 2021, PP (99): 1- 16.
3	HOU F P , ZOU Y L , LIU T H M , et al. Research on cascading faults of hybrid point-to-point power information network based on blockchain[J]. Chinese Journal of Computational Physics, 2023, 40 (5): 633- 642.
4	ZHANG L , WANG L , YUAN X , et al. Decoding the complex free radical cascade by using a DNA framework-based artificial DNA encoder[J]. Angewandte Chemie International Edition, 2021, 60 (19): 10745- 10755. DOI
5	蒋文君, 刘润然, 范天龙, 等. 多层网络级联失效的预防和恢复策略概述[J]. 物理学报, 2020, 69 (8): 81- 91.
6	MOTTER A E , LAI Y C . Cascade-based attacks on complex networks[J]. Physical Review E, 2002, 66 (6): 065102. DOI
7	BULDYREV S V , PARSHANI R , PAUL G , et al. Catastrophic cascade of failures in interdependent networks[J]. Nature, 2010, 464 (7291): 1025- 1028. DOI
8	DONG Y , ZHAO G , MA Y , et al. A novel image encryption scheme based on pseudo-random coupled map lattices with hybrid elementary cellular automata[J]. Information Sciences, 2022, 593, 121- 154. DOI
9	黄爱玲, 徐笑涵, 关伟, 等. 基于加权耦合映像格子的地铁网络稳定性演化研究[J]. 交通运输系统工程与信息, 2021, 21 (3): 140- 149.
10	ZHOU Y , WANG J , YANG H . Resilience of transportation systems: Concepts and comprehensive review[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20 (12): 4262- 4276. DOI
11	MOTTER A E . Cascade control and defense in complex networks[J]. Physical Review Letters, 2004, 93 (9): 98701- 98710. DOI
12	JING K , DU X , SHEN L , et al. Robustness of complex networks: Cascading failure mechanism by considering the characteristics of time delay and recovery strategy[J]. Physica A: Statistical Mechanics and Its Applications, 2019, 534, 122061. DOI
13	REN F , ZHAO T , WANG H . Risk and resilience analysis of complex network systems considering cascading failure and recovery strategy based on coupled map lattices[J]. Mathematical Problems in Engineering, 2015, 2015 (pt.19): 761818.
14	XU S , XIA Y , OUYANG M . Effect of resource allocation to the recovery of scale-free networks during cascading failures[J]. Physica A: Statistical Mechanics and Its Applications, 2020, 540, 123157. DOI
15	DANZIGER M M , BARABASI A L . Recovery coupling in multilayer networks[J]. Nature Communications, 2022, 13 (1): 1- 8.
16	YIN R R , YUAN H , WANG J , et al. Modeling and analyzing cascading dynamics of the urban road traffic network[J]. Physica A: Statistical Mechanics and Its Applications, 2021, 566, 125600.
17	WAN C , YANG Z , ZHANG D , et al. Resilience in transportation systems: A systematic review and future directions[J]. Transport Reviews, 2018, 38 (4): 479- 498.
18	HUANG Y , WU J , REN W , et al. Sequential restorations of complex networks after cascading failures[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018, 51 (1): 400- 411.
19	MAJDANDZIC A , PODOBINK B , BULDYREV S V , et al. Spontaneous recovery in dynamical networks[J]. Nature Physics, 2014, 10 (1): 34- 38.
20	李钊, 郭燕慧, 徐国爱, 等. 复杂网络中带有应急恢复机理的级联动力学分析[J]. 物理学报, 2014, 63 (15): 417- 428.
21	贾春晓, 李明, 刘润然. 多层复杂网络上的渗流与级联失效动力学[J]. 电子科技大学学报, 2022, 51 (1): 148- 160.
22	吴宗柠, 狄增如, 樊瑛. 多层网络的结构与功能研究进展[J]. 电子科技大学学报, 2021, 50 (1): 106- 120.
23	王秋玲, 朱璋元, 陈红, 等. 基于CML的级联失效下异质多层交通网络节点抵抗特性研究[J]. 中国公路学报, 2022, 35 (1): 263- 274.
24	张长富. 基于混沌理论的多安全级别视频加密算法研究与应用[D]. 沈阳: 东北大学, 2016.
25	BRUNEAU M , CHANG S E , EGUCHI R T , et al. A framework to quantitatively assess and enhance the seismic resilience of communities[J]. Earthquake Spectra, 2003, 19 (4): 733- 752.
26	BARABASI A L , ALBERT R . Emergence of scaling in random networks[J]. Science, 1999, 286 (5439): 509- 512.
27	FU T , WU L , LI C G . Site-bond percolation modeling of real networks: Generating function method[J]. Chinese Journal of Computational Physics, 2022, 39 (2): 212- 222.

[1]	邵贝贝, 邹艳丽, 洪少燕, 梁婵娟. 基于复杂网络拓扑的电网Braess悖论现象研究[J]. 计算物理, 2023, 40(6): 770-778.
[2]	付韬, 邬龙, 李晨光. 基于生成函数方法的现实网络座键渗流建模[J]. 计算物理, 2022, 39(2): 212-222.
[3]	张少泽, 邹艳丽, 谭秫毅, 李浩乾, 刘欣妍. 基于复杂网络理论的互联电网Braess悖论现象分析[J]. 计算物理, 2022, 39(2): 233-243.
[4]	李浩乾, 邹艳丽, 张少泽, 刘欣妍, 谭秫毅. 基于复杂网络的电网结构健壮性及Braess悖论现象研究[J]. 计算物理, 2021, 38(4): 470-478.
[5]	王意, 邹艳丽, 黄李, 李可. 综合考虑局部和全局特性的电网关键节点识别[J]. 计算物理, 2018, 35(1): 119-126.
[6]	安海岗. 基于复杂网络的时间序列双变量联动波动[J]. 计算物理, 2014, 31(6): 742-750.
[7]	范文礼, 刘志刚. 一种基于效率矩阵的网络节点重要度评价算法[J]. 计算物理, 2013, 30(5): 714-719.
[8]	唐圣学, 陈丽, 黄姣英. 关联复杂网络建模及辨识研究[J]. 计算物理, 2012, 29(2): 308-316.
[9]	王金兰, 陈光旨. 时空混沌系统的主动-间隙耦合同步[J]. 计算物理, 1999, 16(5): 511-516.