Goos-Hanchen Shift of Electrons Based on Wigner Equation

doi:10.19596/j.cnki.1001-246x.8310

Abstract

Abstract:

We studied transport properties of electrons in two-dimensional electron gas with Wigner equation. It was found that as electrons enter the barrier interface obliquely and are reflected, Goos-Hanchen shift similar to light waves presents. With Wigner equation we get transient evolution of electrons, with which we can calculate Goos-Hanchen shift and study trajectory of electrons inside the potential barrier as well. Compared with Goos-Hanchen shift obtained with the stable phase method, it is found that the interface reflection considering Goos-Hanchen shift has a certain retardation in time compared with geometric optical reflection, which is independent of incident angle, but increases with the increase of width. However, Goos-Hanchen shift of electrons is independent of barrier width and increases with the incident angle or incident energy. According to this, we propose an electron beam splitter model in which Gaussian wave packets with different initial kinetic energies inject into the input. As electron energy is below 0. 01 eV, about 85% of the electrons move to the second output, while as electron energy is above 0. 07 eV, about 85% of the electrons move to the first output.

Key words: Goos-Hanchen shift, Wigner formalism, electron beam splitter, planar nanometer device

CLC Number:

O463

Shouguang CHENG, Yunqian YIN, Julian ZHONG, Kunyuan XU. Goos-Hanchen Shift of Electrons Based on Wigner Equation[J]. Chinese Journal of Computational Physics, 2021, 38(4): 431-440.

Figures/Tables 12

Fig.1 Flowchart of the Wigner Monte Carlo methodbased on signed particles

Table 1 Simulation parameters

L_x/nm	L_y/nm	L_c/nm	Δk/nm^-1	Δl/fs	Δx/nm	Δy/nm	k_x0/nm^-1	σ/nm	势垒宽度a/nm	势垒高度/eV
150	150	100	π/L_c	1.0	1.0	1.5	0.25	10	10	0.05

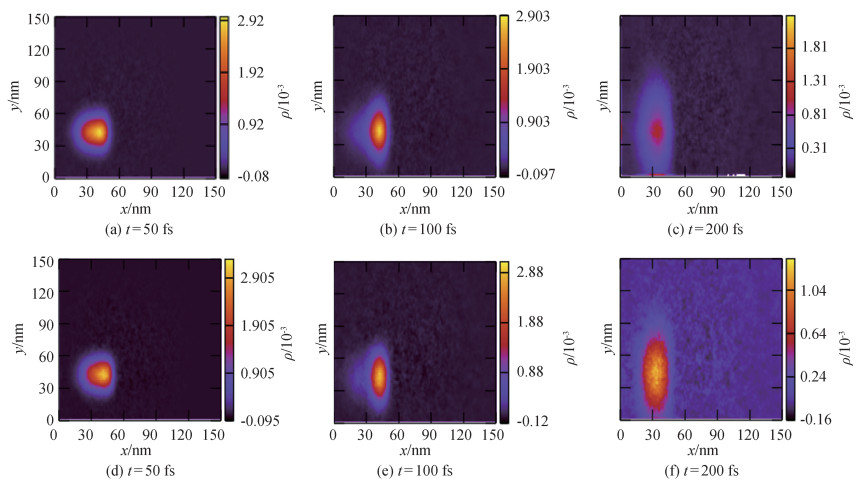
Fig.2 Comparison of optimizing redistribution scheme (a), (b), (c) are density distributions by the original program; (d), (e), (f) represent density distributions after optimization

Table 2 Thread-acceleration ratios of thesquare barrier evolution

线程数	计算时间/s	加速比
1	94 443	1
2	54 627	1.73
3	36 064	2.62
4	30 710	3.08
5	28 684	3.29
6	23 071	4.09
7	21 187	4.45
8	19 285	4.9

Fig.3 Total reflection of light at interface andGoos-Hanchen shift

Fig.4 Total reflection of light and Goos-Hanchen shift

Fig.5 Influence of barrier width on Goos-Hanchen shift

Fig.6 Influence of incident angle on Goos-Hanchen shift

Fig.7 Influence of incident energy on Goos-Hanchen shift

Fig.8 Device structure

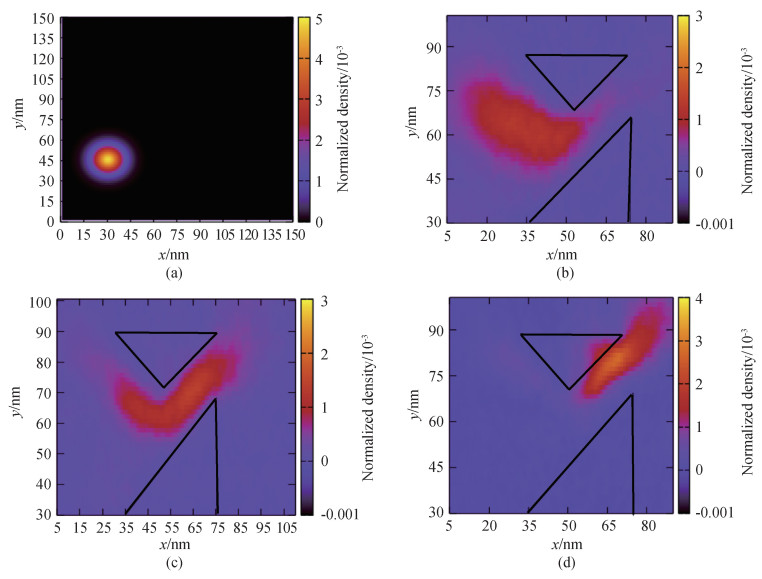
Fig.9 Movement of wave packets with different incident energy at the barrier interface (a) Initial position of the wave packet; (b) Position of a incident kinetic energy E=0.01 eV wave packet at t=270 fs; (c) Position of a incident kinetic energy E=0.028 eV wave packet at t=180 fs; (d) Position of a incident kinetic energy E=0.0 7 eV wave packet at t=140 fs

Fig.10 The ratio of wave packets to two output terminalswith different incident kinetic energy

References 28

1	GOOS F, HÄNCHEN H. Ein neuer und fundamentaler versuch zur total reflexion[J]. Annalen der Physik, 1947, 436 (7-8): 333- 346. DOI
2	GOOS F, HÄNCHEN H. Neumessung des Strahlversetzung seffektes bei total reflexion[J]. Annalen der Physik, 1949, 440 (3-5): 251- 252. DOI
3	ARTMANN K. Berechnung der Seitenversetzung des total reflektierten Strahles[J]. Annalen der Physik, 1948, 437 (1-2): 87- 102. DOI
4	RENARD R H. Total reflection: A new evaluation of the Goos-Hänchen shift[J]. Journal of the Optical Society of America, 1964, 54 (10): 1190- 1197. DOI
5	YU Z M, LIU Y, YANG S A. Anomalous spatial shifts in interface electronic scattering[J]. Frontiers of Physics, 2019, 14 (3): 33402. DOI
6	BLIOKH K Y, AIELLO A. Goos-Hänchen and Imbert-Fedorov beam shifts: An overview[J]. Journal of Optics, 2013, 15 (1): 014001. DOI
7	SINITSYN N A, NIU Q, SINOVA J, et al. Disorder effects in the anomalous Hall effect induced by Berry curvature[J]. Physical Review B, 2005, 72 (4): 045346. DOI
8	BALLICCHIA M, WEINBUB J, NEDJALKOV . Electron evolution around a repulsive dopant in a quantum wire: Coherence effects[J]. Nanoscale, 2018, 10 (48): 23037- 23049. DOI
9	SELLIER J M, KAPANOVA K G. A study of entangled systems in the many-body signed particle formulation of quantum mechanics[J]. International Journal of Quantum Chemistry, 2017, 117 (23): e25447. DOI
10	WIGNER E P. On the quantum correction for thermodynamic equilibrium[J]. Physical Review, 1932, 40, 749. DOI
11	SELLIER J M. A signed particle formulation of non-relativistic quantum mechanics[J]. Journal of Computational Physics, 2015, 297, 254- 265. DOI
12	SELLIER J M, NEDJALKOV M, DIMOV I, et al. A benchmark study of the Wigner Monte Carlo method[J]. Monte Carlo Methods and Applications, 2014, 20 (1): 43- 51.
13	WEINBUB J, FERRY D K. Recent advances in Wigner function approaches[J]. Applied Physics Reviews, 2018, 5 (4): 041104. DOI
14	KIM K Y, LEE B. On the high order numerical calculation schemes for the Wigner transport equation[J]. Solid-State Electronics, 1999, 43 (12): 2243- 2245. DOI
15	KIM K Y, KIM S, TANG T. Accuracy balancing for the finite-difference-based solution of the discrete Wigner transport equation[J]. Journal of Computational Electronics, 2017, 16 (1): 148- 154. DOI
16	SHAO S, LU T, CAI W. Adaptive conservative cell average spectral element methods for transient Wigner equation in quantum transport[J]. Communications in Computational Physics, 2011, 9 (3): 711- 739. DOI
17	SCHULZ L, SCHULZ D. Application of a slowly varying envelope function onto the analysis of the Wigner transport equation[J]. IEEE Transactions on Nanotechnology, 2016, 15 (5): 801- 809. DOI
18	LEE J H, SHIN M. Quantum transport simulation of nanowire resonant tunneling diodes based on a Wigner function model with spatially dependent effective masses[J]. IEEE Transactions on Nanotechnology, 2017, 16 (6): 1028- 1036. DOI
19	DORDA A, SCHURRER F. A WENO-solver combined with adaptive momentum discretization for the Wigner transport equation and its application to resonant tunneling diodes[J]. Journal of Computational Physics, 2015, 284, 95- 116. DOI
20	SHIFREN L, FERRY D. A Wigner function based ensemble Monte Carlo approach for accurate incorporation of quantum effects in device simulation[J]. Journal of Computational Electronics, 2002, 1 (1-2): 55- 58.
21	ELLINGHAUS P, NEDJALKOV M, SELBERHERR S. The influence of electrostatic lenses on wave packet dynamics[C]. International Conference on Large-Scale Scientific Computing, Springer, Cham, 2015: 277-284.
22	LI Gang, ZHANG Baoyin, DENG Li, SHANGGUAN Danhua, et al. Pseudo-random numbers for identical results on varying numbers of processors in domain decomposed particle Monte Carlo simulations[J]. Chinese J Comput Phys, 2017, 34 (1): 67- 72.
23	XU Haiyan, HUANG Zhengfeng, CAI Shaohui. Global variance reduction method for Monte Carlo particle transport problemes[J]. Chinese J Comput Phys, 2010, 27 (5): 722- 732.
24	HU Xiaoyan, CAO Xiaolin, GUO Hong, et al. Parallel algorithm of coupled Fourier transform and fluid numerical computation[J]. Chinese J Comput Phys, 2012, 29 (4): 484- 488.
25	ELLINGHAUS P. Two-dimensional Wigner Monte Carlo simulation for time-resolved quantum transport with scattering[D]. Vienna: Universität Wien, 2016.
26	CHEN X, LI C F, BAN Y. Novel shift in transmission through a two-dimensional semiconductor barrier[J]. Physics Letters A, 2006, 354 (1/2): 161- 165.
27	BOCQUILLON E, PARMENTIER F D, GRENIER C, et al. Electron quantum optics: Partitioning electrons one by one[J]. Physical Review Letters, 2012, 108 (19): 196803. DOI
28	ELLINGHAUS P, WEINBUB J, NEDJALKOV M, et al. Analysis of lense-governed Wigner signed particle quantum dynamics[J]. Physica Status Solidi-Rapid Research Letters, 2017, 11 (7): 1700102. DOI

[1]	XU Xiaodong, ZHOU Bin, GUO Jinchuan, YI Minghao, XIAO Feihu. Monte Carlo Simulation of Interaction of Electrons with Anode in Microstructure X-Ray Tubes [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(1): 95-102.
[2]	LI Chaolong, SHI Haiquan, LÜ Jianqin. Simulation of Intense Beam Transfer in Double-Cylinder Accelerate Lens [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2013, 30(3): 403-408.
[3]	Wang Liping, Tang Tiantong. An automatic differentiation technique: differential algebra and its application in charged particle optics [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 1999, 16(3): 225-234.
[4]	Zhou Qing, Chen Ergang, Hu Zonggao. COMPUTATION AND ANALYSIS OF A MAGNETIC SEXTUPOLE SYSTEM FOR CORRECTION OF SPHERICAL ABERRATION [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 1997, 14(S1): 485-486.
[5]	Song Zhitang, Liu Chunliang, Xia Huiqin. ANALYTICAL EXPRESSIONS OF AXIAL THIRD ORDER CHROMATIC DISPERSION ABERRATION COEFFICIENTS OF CIRCULAR ELECTRIC FIELD [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 1997, 14(3): 368-374.
[6]	Lei Wei, Tong Linsu. SIMULATION OF ELECTRON OPTICAL SYSTEM IN COLOR MONITOR TUBES [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 1996, 13(3): 323-332.