Chinese Journal of Computational Physics ›› 2024, Vol. 41 ›› Issue (3): 287-297.DOI: 10.19596/j.cnki.1001-246x.8723
Previous Articles Next Articles
Received:2023-03-09
Online:2024-05-25
Published:2024-05-25
CLC Number:
Xiong TANG, Pei ZHENG. Finite Deformation Theory of Poroviscoelasticity Based on Logarithmic Strain[J]. Chinese Journal of Computational Physics, 2024, 41(3): 287-297.
Add to citation manager EndNote|Ris|BibTeX
URL: http://www.cjcp.org.cn/EN/10.19596/j.cnki.1001-246x.8723
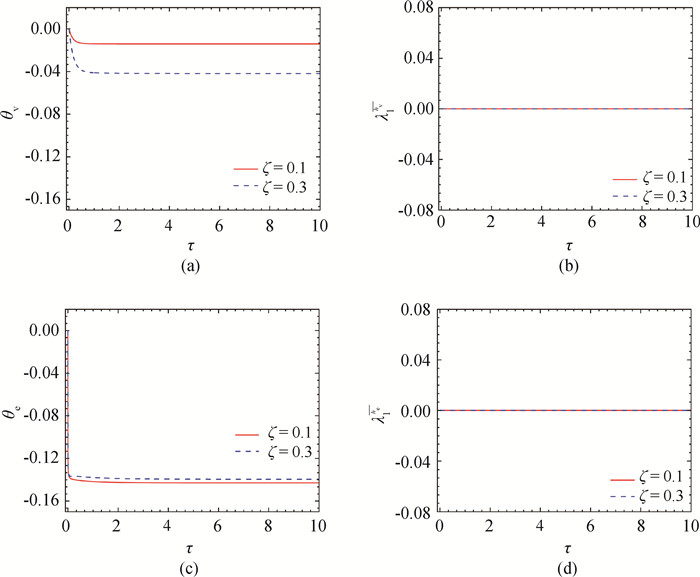
Fig.4 Evolution curves of logarithmic strain of viscous and elastic part with different ratios ofζ(a) viscous volumetric component of logarithmic strainθv; (b) stretch of viscous deviatoric component of logarithmic strain $\lambda_1^{\overline{\boldsymbol{h}}_{\mathrm{v}}}$; (c) elastic volumetric component of logarithmic strainθe; (d) stretch of elastic deviatoric component of logarithmic strain $\lambda_1^{\overline{\boldsymbol{h}}_{\mathrm{e}}}$
| 1 |
ZHENG Pei , TANG Xiong , ZHANG Keming . A finite strain poroviscoelastic model based on the logarithmic strain[J]. European Journal of Mechanics-A/Solids, 2022, 96, 104679.
DOI |
| 2 |
BIOT M A . Theory of deformation of a porous viscoelastic anisotropic solid[J]. Journal of Applied Physics, 1956, 27 (5): 459- 467.
DOI |
| 3 |
BIOT M A . Mechanics of deformation and acoustic propagation in porous media[J]. Journal of Applied Physics, 1962, 33 (4): 1482- 1498.
DOI |
| 4 |
BIOT M A . Nonlinear and semilinear rheology of porous solids[J]. Journal of Geophysical Research, 1973, 78 (23): 4924- 4937.
DOI |
| 5 | COUSSY O . Poromechanics[M]. 2nd ed Chichester: Wiley, 2004. |
| 6 |
MOW V C , KUEI S C , LAI W M , et al. Biphasic creep and stress relaxation of articular cartilage in compression? Theory and experiments[J]. Journal of Biomechanical Engineering, 1980, 102 (1): 73- 84.
DOI |
| 7 |
EHLERS W , MARKERT B . A linear viscoelastic biphasic model for soft tissues based on the theory of porous media[J]. Journal of Biomechanical Engineering, 2001, 123 (5): 418- 424.
DOI |
| 8 |
HU Yuhang , SUO Zhigang . Viscoelasticity and poroelasticity in elastomeric gels[J]. Acta Mechanica Solida Sinica, 2012, 25 (5): 441- 458.
DOI |
| 9 | COUSSY O . Mechanics and physics of porous solids[M]. Chichester: Wiley, 2010. |
| 10 |
WANG Xiao , HONG Wei . A visco-poroelastic theory for polymeric gels[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2012, 468 (2148): 3824- 3841.
DOI |
| 11 |
HE Dongjing , HU Yuhang . Nonlinear visco-poroelasticity of gels with different rheological parts[J]. Journal of Applied Mechanics, 2020, 87 (7): 071010.
DOI |
| 12 |
ZHENG Pei , TANG Xiong , ZHANG Keming . On constitutive modelling of linear poroviscoelastic solids[J]. International Journal of Engineering Science, 2022, 178, 103728.
DOI |
| 13 | HENCKY H . Vber die Form des Elastizit¨atsgesetzes bei ideal elastischen Stoffen[J]. Zeitschrift für Technische Physik, 1928, 9 (1): 215- 220. |
| 14 |
ANAND L . On H. Hencky's approximate strain-energy function for moderate deformations[J]. Journal of Applied Mechanics, 1979, 46 (1): 78- 82.
DOI |
| 15 |
ANAND L . Moderate deformations in extension-torsion of incompressible isotropic elastic materials[J]. Journal of the Mechanics and Physics of Solids, 1986, 34 (3): 293- 304.
DOI |
| 16 |
MONTELLA G , GOVINDJEE S , NEFF P . The exponentiated Hencky strain energy in modeling tire derived material for moderately large deformations[J]. Journal of Engineering Materials and Technology, 2016, 138 (3): 031008.
DOI |
| 17 |
ANAND L . A large deformation poroplasticity theory for microporous polymeric materials[J]. Journal of the Mechanics and Physics of Solids, 2017, 98, 126- 155.
DOI |
| 18 |
FLORY P J . Thermodynamic relations for high elastic materials[J]. Transactions of the Faraday Society, 1961, 57, 829- 838.
DOI |
| 19 |
OGDEN R W . Nearly isochoric elastic deformations: Application to rubberlike solids[J]. Journal of the Mechanics and Physics of Solids, 1978, 26 (1): 37- 57.
DOI |
| 20 |
HENCKY H . The law of elasticity for isotropic and quasi-isotropic substances by finite deformations[J]. Journal of Rheology, 1931, 2 (2): 169- 176.
DOI |
| 21 | XIAO H , CHEN L S . Hencky's elasticity model and linear stress-strain relations in isotropic finite hyperelasticity[J]. Acta Mechanica, 2002, 157 (1/4): 51- 60. |
| 22 |
NEFF P , EIDEL B , MARTIN R J . Geometry of logarithmic strain measures in solid mechanics[J]. Archive for Rational Mechanics and Analysis, 2016, 222 (2): 507- 572.
DOI |
| 23 |
BORJA R I . On the mechanical energy and effective stress in saturated and unsaturated porous continua[J]. International Journal of Solids and Structures, 2006, 43 (6): 1764- 1786.
DOI |
| 24 |
ZHENG Pei , JIAO Guyue , ZHANG Keming . A mixed stabilized finite element formulation for finite deformation of a poroelastic solid saturated with a compressible fluid[J]. Archive of Applied Mechanics, 2020, 90 (5): 1097- 1115.
DOI |
| 25 |
GAJO A . A general approach to isothermal hyperelastic modelling of saturated porous media at finite strains with compressible solid constituents[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2010, 466 (2122): 3061- 3087.
DOI |
| 26 |
NEDJAR B . Formulation of a nonlinear porosity law for fully saturated porous media at finite strains[J]. Journal of the Mechanics and Physics of Solids, 2013, 61 (2): 537- 556.
DOI |
| 27 |
HUBER N , TSAKMAKIS C . Finite deformation viscoelasticity laws[J]. Mechanics of Materials, 2000, 32 (1): 1- 18.
DOI |
| 28 |
COLEMAN B D , GURTIN M E . Thermodynamics with internal state variables[J]. Journal of Chemical Physics, 1967, 47 (2): 597- 613.
DOI |
| 29 | REESE S , GOVINDJEE S . A theory of finite viscoelasticity and numerical aspects[J]. International Journal of Solids and Structures, 1998, 35 (26/27): 3455- 3482. |
| 30 |
SHUTOV A V , LANDGRAF R , IHLEMANN J . An explicit solution for implicit time stepping in multiplicative finite strain viscoelasticity[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 265, 213- 225.
DOI |
| 31 |
LATORRE M , MONTÁNS F J . Anisotropic finite strain viscoelasticity based on the Sidoroff multiplicative decomposition and logarithmic strains[J]. Computational Mechanics, 2015, 56 (3): 503- 531.
DOI |
| 32 | LATORRE M , MONTÁNS F J . Fully anisotropic finite strain viscoelasticity based on a reverse multiplicative decomposition and logarithmic strains[J]. Computers & Structures, 2016, 163, 56- 70. |
| 33 | CHENG A H D . Poroelasticity[M]. Switzerland: Springer, 2016. |
| 34 |
CHESTER S A , DI LEO C V , ANAND L . A finite element implementation of a coupled diffusion-deformation theory for elastomeric gels[J]. International Journal of Solids and Structures, 2015, 52, 1- 18.
DOI |
| 35 |
朱家莉, 尚月强. 不可压缩流的并行两水平稳定有限元算法[J]. 计算物理, 2022, 39 (3): 309- 317.
DOI |
| 36 | 张娜, 姚军, 黄朝琴, 等. 多孔介质两相流的局部守恒有限元分析[J]. 计算物理, 2013, 30 (5): 667- 674. |
| 37 |
陈恭, 王一正, 王烨, 等. 缩减基有限元方法快速求解参数化偏微分方程[J]. 计算物理, 2018, 35 (5): 515- 524.
DOI |
| [1] | TAN Mei-lan, WANG Xin-wei, GAN Li-fei. Buckling of a Spatial Elastic Thin Rod Under Torque [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2006, 23(4): 447-450. |
| [2] | LI Jiang-hai, SUN Qin. Constructing a Class of Orthogonal-reinforced Hierarchical Hexahedra Vector FE [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2006, 23(1): 32-36. |
| [3] | Chen Chuping, Y. S. Li. AN OPERATOR-SPLITING METHOD FOR NUMERICAL MODELLING OFTRANSPORTATION PROBLEM [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 1990, 7(4): 415-423. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||
Copyright © Chinese Journal of Computational Physics
E-mail: jswl@iapcm.ac.cn
Supported by Beijing Magtech Co., Ltd.

